Với giải sách bài tập Toán 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
a) SB và (ABCD);
b) SC và (ABCD);
c) SD và (ABCD);
d) SB và (SAC).
Lời giải:
a) Ta có:
Suy ra AB là hình chiếu của SB trên (ABCD).
Do đó (SB, (ABCD)) = (SB, AB).
Trong tam giác SAB vuông tại A, ta có:
Vậy
b) Tương tự câu a) ta xác định được (SC, (ABCD)) = (SC, AC).
Trong tam giác SAC vuông tại A, ta có:
Vậy
c) Tương tự câu a) ta xác định được (SD, (ABCD)) = (SD,AD).
Trong tam giác SAD vuông tại A, ta có:
Vậy
d) Ta có:
BD ⊥ (SAC) hay BO ⊥ (SAC). (1)
Mà SB (SAC) = S. (2)
Từ (1) và (2) suy ra SO là hình chiếu của SB trên (SAC).
Do đó: (SB, (SAC))=(SB, SO).
Trong tam giác SBO vuông tại O, ta có:
Vậy
a) SA và (ABC);
b) SC và (SAB).
Lời giải:
a)Vì AI là hình chiếu của SA trên (ABC).
Do đó (SA, (ABC)) = (SA, AI).
Vì tam giác SAI vuông cân tại I
Vậy .
b)Ta có tam giác ABC đều nên CI ⊥ AB,
Ta có:
Mà SC (SAB) = S. (2)
Từ (1) và (2) SI là hình chiếu của SC trên (SAB).
Do đó (SC, (SAB)) = (SC, SI).
Trong tam giác SAB vuông tại S, .
Trong tam giác SCI vuông tại I, ta có
Vậy
Lời giải:
Gọi M là trung điểm BC, G là trọng tâm tam giác ABC.
Ta có SG ⊥ (ABC), SM ⊥ BC, AM ⊥ BC.
Suy ra là góc phẳng nhị diện [S, BC, A].
Ta tính được
GM = SG.
Ta có tam giác SMG vuông cân tại G, suy ra số đo góc phẳng nhị diện [S, BC, A] =
Lời giải:
Vẽ AH ⊥ BC (H ϵ BC), ta có SH ⊥ BC.
Suy ra là góc phẳng nhị diện [S, BC, A].
Ta có AH = AC.sin60° = = SA
Do đó = 45°.
Xem thêm các bài giải SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Khoảng cách trong không gian
Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 1: Biến cố giao và quy tắc nhân xác suất
Bài 2: Biến cố hợp và quy tắc cộng xác suất
Lý thuyết Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
1. Góc giữa đường thẳng và mặt phẳng
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng .
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).
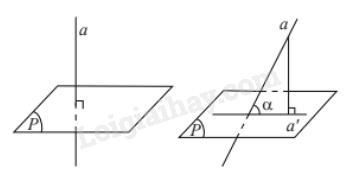
Chú ý:
a) Góc giữa đường thẳng và mặt phẳng luôn thỏa mãn .
b) Nếu đường thẳng a nằm trong (P) hoặc a song song với (P) thì .
2. Góc nhị diện và góc phẳng nhị diện
Góc nhị diện
Cho hai nửa mặt phẳng và có chung bờ là đường thẳng d. Hình tạo bởi , và d được gọi là góc nhị diện tạo bởi và , kí hiệu .
Hai nửa mặt phẳng , gọi là hai mặt của nhị diện và d gọi là cạnh của nhị diện.
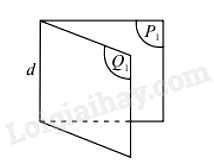
Chú ý:
a) Hai mặt phẳng cắt nhau theo giao tuyến d tạo thành bốn góc nhị diện.
b) Góc nhị diện còn được kí hiệu là với M, N tương ứng thuộc hai nửa mặt phẳng .
Góc phẳng nhị diện
Góc phẳng nhị diện của góc nhị diện là góc có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.
Chú ý:
a) Đối với một góc nhị diện, các góc phẳng nhị diện đều bằng nhau.
b) Nếu mặt phẳng (R) vuông góc với cạnh d của góc nhị diện và cắt hai mặt của góc nhị diện theo hai nửa đường thẳng Ou và Ov thì là góc phẳng nhị diện của góc nhị diện tạo bởi .
c) Góc nhị diện có góc phẳng nhị diện là góc vuông được gọi là góc nhị diện vuông.
d) Số đo góc phẳng nhị diện được gọi là số đo góc nhị diện.
e) Số đo góc nhị diện nhận giá trị từ đến .