Với giải Bài 7.19 trang 34 SBT Toán lớp 11 Kết nối tri thức chi tiết trong Bài 25: Hai mặt phẳng vuông góc giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán lớp 11 Bài 25: Hai mặt phẳng vuông góc
Bài 7.19 trang 34 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD có độ dài các cạnh bằng a. Gọi M là trung điểm của CD, kẻ AH vuông góc với BM tại H.
a) Chứng minh rằng AH (BCD).
b) Tính côsin của góc giữa mặt phẳng (BCD) và mặt phẳng (ACD).
Lời giải:
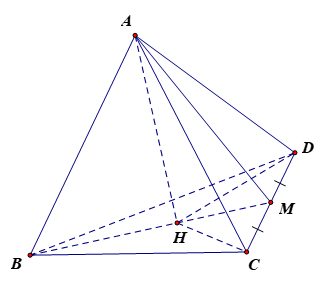
a) Vì M là trung điểm của CD nên BM là trung tuyến.
Vì BCD là tam giác đều nên CD BM.
Tương tự CD AM nên CD (ABM), suy ra CD ^ AH.
Mà AH BM nên AH (BCD).
b) Vì AM CD, BM CD nên góc giữa hai mặt phẳng (BCD) và mặt phẳng (ACD) bằng góc giữa hai đường thẳng AM và BM, mà (AB,BM) = .
Tam giác BCD đều có BM là đường cao đồng thời là trung tuyến, ta chứng minh được H là trọng tâm tam giác BCD nên BM = và HM = BM = .
Tam giác ADC đều có AM là đường cao đồng thời là trung tuyến nên AM = .
Xét tam giác AHM vuông tại H nên cos = cos.
Vậy côsin của góc giữa mặt phẳng (BCD) và mặt phẳng (ACD) bằng .
Xem thêm lời giải sách bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 7.23 trang 34 SBT Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.....
Xem thêm các bài giải SBT Toán 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
