Với giải sách bài tập Toán 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán lớp 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng
Lời giải:
Kẻ AH (BCD) tại H, ta có BH là hình chiếu vuông góc của AB trên mặt phẳng (BCD) nên góc giữa đường thẳng AB và mặt phẳng (BCD) bằng góc giữa hai đường AB và BH, mà (AB, BH) = .
Vì AB = AC = AD nên HD = HB = HC hay H là tâm của tam giác BCD.
Gọi M là giao điểm của BH là CD.
Vì tam giác BCD đều cạnh a nên BM là đường cao, trung tuyến và BM = , suy ra BH = BM = .
Xét tam giác ABH vuông tại H có: cos = = .
Vậy côsin của góc giữa đường thẳng AB và mặt phẳng (BCD) bằng .
a) Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
b) Tính tang của góc giữa đường thẳng SC và mặt phẳng (SAB).
Lời giải:
a) Vì SA (ABCD) nên AC là hình chiếu vuông góc của SC trên mặt phẳng (ABCD). Do đó góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng SC và AC, mà (SC, AC) = .
Do ABCD là hình vuông cạnh a nên AC2 = AB2 + BC2 = 2a2 ⇒ AC = a.
Vì SA (ABCD) nên SA AC mà SA = AC = a nên tam giác SAC vuông cân tại A. Do đó = 45o.
Vậy góc giữa đường thẳng SC và mặt phẳng (ABCD) là 45°.
b) Vì SA (ABCD) nên BC SA mà BC AB nên BC (SAB), suy ra SB là hình chiếu vuông góc của SC trên mặt phẳng (SAB).
Do đó, góc giữa đường thẳng SC và mặt phẳng (SAB) bằng góc giữa đường thẳng SC và đường thẳng SB, mà (SB,SC) = .
Xét tam giác SAB vuông tại A, có SB =
Xét tam giác SBC vuông tại B, ta có: tan = .
Vậy tang của góc giữa đường thẳng SC và mặt phẳng (SAB) bằng .
a) Tính tang của góc giữa đường thẳng SB và mặt phẳng (SAC).
b) Tính sin của góc giữa đường thẳng AC và mặt phẳng (SBC).
Lời giải:
a) Kẻ BH AC tại H, mà SA (ABC) nên SA BH nên BH (SAC).
Do đó SH là hình chiếu vuông góc của SB trên mặt phẳng (SAC). Khi đó góc giữa đường thẳng SB và mặt phẳng (SAC) bằng góc giữa hai đường thẳng SB và SH, mà (SH,SB) = .
Xét tam giác ABC vuông cân tại B, BH AC, ta có:
.
Xét tam giác ABH vuông tại H, có:
AB2 = BH2 + AH2 a2 = +AH2 AH2 = .
Vì SA (ABC) nên SA AC.
Xét tam giác SAH vuông tại A, có
SA2 + AH2 = SH2 (a)2 + = SH2 SH = .
Vì BH (SAC) nên BH SH.
Xét tam giác SHB vuông tại H, có tan = = .
Vậy tang của góc giữa đường thẳng SB và mặt phẳng (SAC) là .
b) Kẻ AK SB tại K.
Có SA (ABC) nên SA BC mà tam giác ABC vuông tại B nên BC AB.
Do đó BC (SAB) nên BC AK , suy ra AK (SBC).
Do đó CK là hình chiếu vuông góc của AC trên (SBC), suy ra góc giữa đường thẳng AC và mặt phẳng (SBC) bằng góc giữa hai đường thẳng AC và CK, mà (AC,CK) = .
Xét tam giác SAB vuông tại A, AK SB, có:
SB = ;
SA.AB = SB.AK AK = = a.
Do tam giác ABC vuông cân tại B nên AC = .
Vì AK (SBC) nên AK CK.
Xét tam giác ACK vuông tại K, có sin.
Vậy sin của góc giữa đường thẳng AC và mặt phẳng (SBC) là .
Lời giải:
Gọi O là giao điểm của A'C' và B'D'.
Khi đó, O là trung điểm của A'C' và B'D'.
Theo đề bài ta có O là hình chiếu của A trên mặt phẳng (A'B'C'D').
Do đó, A'O là hình chiếu vuông góc của AA' trên mặt phẳng (A'B'C'D'). Khi đó góc giữa đường thẳng AA' và mặt phẳng (A'B'C'D') bằng góc giữa AA' và A'O. Mà (AA',A'O) = .
Vì hình hộp ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a nên A'B'C'D' là hình vuông cạnh a. Do đó A'C'2 = A'B'2 + B'C'2 = a2 + a2 = 2a2 ⇒ A'C' = a.
A'O = .
Xét tam giác AOA' vuông tại O, có cos = = 60o.
Vậy góc giữa đường thẳng AA' và mặt phẳng (A'B'C'D') bằng 60°.
a) Chứng minh rằng SO (ABCD).
b) Tính góc giữa đường thẳng SA và mặt phẳng (SBD).
c) Gọi M là trung điểm của cạnh SC và là góc giữa đường thẳng OM và mặt phẳng (SBC). Tính sin.
Lời giải:
a) Có O là trung điểm của AC, BD.
Vì SA = SC nên tam giác SAC là tam giác cân mà SO là trung tuyến nên SO là đường cao hay SO AC.
Tương tự SO BD. Do đó SO (ABCD).
b) Vì SO (ABCD) nên SO AO.
Lại có AO BD (do ABCD là hình vuông). Do đó AO (SBD).
Suy ra SO là hình chiếu vuông góc của SA trên mặt phẳng (SBD). Do đó góc giữa đường thẳng SA và mặt phẳng (SBD) bằng góc giữa hai đường thẳng SA và SO.
Mà (SA,SO) = .
Xét tam giác ABC vuông tại B, có AC2 = AB2 + BC2 = a2 + a2 = 2a2.
Có SA2 + SC2 = a2 + a2 = 2a2, suy ra AC2 = SA2 + SC2. Do đó tam giác ASC vuông tại S mà SA = SC nên tam giác ASC vuông cân tại S.
Xét tam giác vuông cân ASC tại S có SO là đường cao nên SO là phân giác. Do đó = 45o .
Vậy góc giữa đường thẳng SA và mặt phẳng (SBD) bằng 45°.
c) Kẻ OK BC tại K, OH SK tại H.
Có BC OK (cách vẽ), BC SO (SO (ABCD)). Do đó BC (SOK), suy ra BC OH mà OH SK nên OH (SBC).
Suy ra, HM là hình chiếu vuông góc của OM trên mặt phẳng (SBC), do đó góc giữa đường thẳng OM và mặt phẳng (SBC) bằng góc giữa hai đường thẳng OM và MH, mà (OM,MH) = .
Do tam giác SOC vuông tại O, OM là trung tuyến nên OM = .
Xét tam giác ABC có OK là đường trung bình nên OK = .
Xét tam giác SAC vuông tại S, có .
Xét tam giác SOK vuông tại O, có .
Xét tam giác OHM vuông tại H, có sin = sin.
Vậy sin = .
Lời giải:
Gọi A là vị trí con diều, B là vị trí đầu dây diều trên mặt đất, H là hình chiếu vuông góc của A trên mặt đất.
Xét tam giác ABH vuông tại H, = 60o, AB = 10 m = 1 000 cm.
Ta có AH = AB . sin60° 866 (cm).
Vậy hình chiếu vuông góc trên mặt đất của con diều cách đầu dây diều trên mặt đất khoảng 866 centimét.
Xem thêm các bài giải SBT Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 23: Đường thẳng vuông góc với mặt phẳng
Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng
Bài 25: Hai mặt phẳng vuông góc
Lý thuyết Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng
1. Phép chiếu vuông góc
Phép chiếu vuông góc lên mặt phẳng (P) theo phương vuông góc với (P) được gọi là phép chiều vuông góc lên mặt phẳng (P).
Chú ý:
- Vì phép chiếu vuông góc lên một mặt phẳng là một trường hợp đặc biệt của phép chiếu song song nên nó có mọi tính chất của phép chiếu song song.
- Phép chiếu vuông góc lên mặt phẳng (P) còn được gọi đơn giản là phép chiếu lên mặt phẳng (P). Hình chiếu vuông góc H’ của hình H trên mặt phẳng (P) còn được gọi là hình chiếu của H trên mặt phẳng (P).
Định lí ba đường vuông góc:
Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Khi đó, một đường thẳng b nằm trong mặt phẳng (P) vuông góc với đường thẳng a khi và chỉ khi b vuông góc với hình chiếu vuông góc a’ của a trên (P).
2. Góc giữa đường thẳng và mặt phẳng
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng .
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).
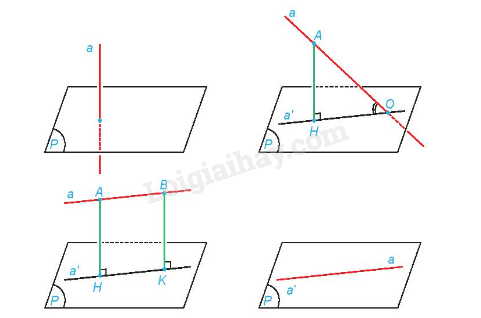
Chú ý: Nếu là góc giữa đường thẳng a và mặt phẳng (P) thì .
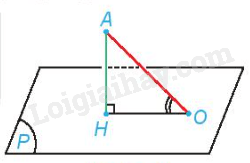
Nhận xét: Nếu điểm A có hình chiếu H trên mặt phẳng (P). Lấy điểm O thuộc mặt phẳng (P), O không trung H. Khi đó góc giữa đường thẳng AO và mặt phẳng (P) bằng góc AOH.