Với giải Bài 8 trang 42 SBT Toán lớp 8 Chân trời sáng tạo chi tiết trong Bài 1: Định lí Thalès trong tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 1: Định lí Thalès trong tam giác
Bài 8 trang 42 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A và MN // BC (M ∈ AB; N ∈ AC). Cho biết AB = 9 cm, AM = 3 cm, AN = 4 cm. Tính độ dài NC, MN, BC.
Lời giải:
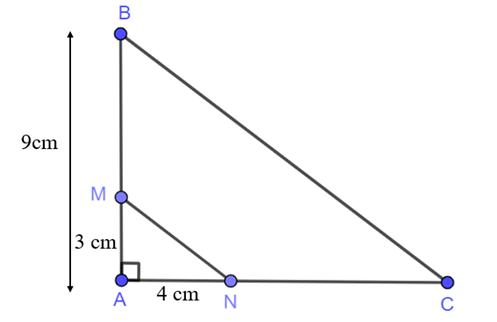
Ta có BM = AB – AM = 9 – 3 = 6 (cm)
Xét ∆ABC có MN // BC nên theo định lí Thalès, ta có .
Suy ra NC = = 8 (cm)
Xét ∆AMN vuông tại A, áp dụng định lý Pythagore, ta có:
MN2 = AM2 + AN2 = 32 + 42 = 25.
Do đó MN = 5 cm.
Xét ∆ABC có MN // BC, theo hệ quả của định lí Thalès, ta có .
Suy ra BC = = 15 (cm).
Vậy NC = 8 cm, MN = 5 cm, BC = 15 cm.
Xem thêm lời giải sách bài tập Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 4 trang 42 sách bài tập Toán 8 Tập 2: Tính các độ dài x, y trong Hình 11....
Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
