Giải SGK Toán 8 Bài 1 (Chân trời sáng tạo): Định lí Thalès trong tam giác

Van Anh Ngày: 23-09-2024 Lớp 8

3.1 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 1: Định lí Thalès trong tam giác chi tiết sách Toán 8 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 1: Định lí Thalès trong tam giác

Giải Toán 8 trang 44 Tập 2

Khởi động trang 44 Toán 8 Tập 2: Những sợi cáp treo của cầu Thuận Phước (thuộc thành phố Đà Nẵng) cho ta hình ảnh những đoạn thẳng song song. Các đoạn thẳng AA', AB', CC' thể hiện ba sợi cáp của cầu. Nếu biết độ dài các đoạn AB, BC, A'B' có thể tính độ dài B'C' không?

Khởi động trang 44 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Sau khi học xong bài này, chúng ta sẽ có thêm kiến thức về đoạn thẳng tỉ lệ từ đó có thể tính được độ dài đoạn B'C' khi biết độ dài của các đoạn AB, BC, A'B'.

1. Đoạn thẳng tỉ lệ

Khám phá 1 trang 44 Toán 8 Tập 2: a) Cho hai số 5 và 8. Hãy tính tỉ số giữa hai số đã cho.

b) Hãy đo và tính tỉ số giữa hai độ dài (theo mm) của hai đoạn thẳng AB và CD trong Hình 1.

Khám phá 1 trang 44 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Tỉ số giữa hai số 5 và 8 là $\frac{5}{8}$

b) Độ dài đoạn AB là 3,5cm

Độ dài đoạn CD là 4,5 cm

Tỉ số của hai đoạn AB và CD là $\frac{A B}{C D} = \frac{3, 5}{4, 5} = \frac{7}{9}$

Thực hành 1 trang 44 Toán 8 Tập 2: Hãy tính tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau:

a) AB = 6 cm; CD = 8 cm;

b) AB = 1,2 m; CD = 42 cm.

Lời giải:

a) Ta có: $\frac{A B}{C D} = \frac{6}{8} = \frac{3}{4}$

b) Đổi AB = 1,2 m = 120 cm

Ta có: $\frac{A B}{C D} = \frac{120}{42} = \frac{20}{7}$

Giải Toán 8 trang 45 Tập 2

Khám phá 2 trang 45 Toán 8 Tập 2: So sánh tỉ số của hai đoạn thẳng AB và CD với tỉ số của hai đoạn thẳng EF và MN trong Hình 2

Khám phá 2 trang 45 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Ta có: $\frac{A B}{C D} = \frac{2}{3}$

$\frac{E F}{M N} = \frac{4}{6} = \frac{2}{3}$

Suy ra $\frac{A B}{C D} = \frac{E F}{M N}$ .

Thực hành 2 trang 45 Toán 8 Tập 2: Trong hình 3, chứng minh rằng:

a) AB và BC tỉ lệ với A'B' và B'C'.

b) AC và A'C' tỉ lệ với AB và A'B'.

Thực hành 2 trang 45 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Theo giả thiết: BB' // CC', AC và A'C' cắt BB' và CC' suy ta ta có:

$\frac{A B}{B C} = \frac{A' B'}{B' C'}$

Vậy hai đoạn thẳng AB và BC tỉ lệ A'B' và B'C'.

b) Theo giả thiết: BB' // CC', AC và A'B' cắt BB' và CC' suy ra ta có:

$\frac{A B}{A C} = \frac{A' B'}{A' C'}$ suy ra $\frac{A C}{A' C'} = \frac{A B}{A' B'}$

Vậy hai đoạn thẳng AC và A'C' tỉ lệ với AB và A'B'.

Vận dụng 1 trang 45 Toán 8 Tập 2: Hãy tìm các đoạn thẳng tỉ lệ trong hình vẽ sơ đồ một góc công viên ở Hình 4.

Vận dụng 1 trang 45 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Ta có: $\frac{A D}{A B} = \frac{1, 5}{4, 5} = \frac{1}{3}$ ; $\frac{A E}{A C} = \frac{3}{9} = \frac{1}{3}$

$\frac{A D}{D B} = \frac{1, 5}{3} = \frac{1}{2}$ ; $\frac{A E}{E C} = \frac{3}{6} = \frac{1}{2}$

Các đoạn thẳng tỉ lệ trong hình vẽ sơ đồ một góc công viên ở Hình 4 là:

$\frac{A D}{A B} = \frac{A E}{A C} = \frac{1}{3}$ ;

$\frac{A D}{D B} = \frac{A E}{E C} = \frac{1}{2}$ .

2. Định lí Thales trong tam giác

Khám phá 3 trang 45 Toán 8 Tập 2: Trên một tờ giấy kẻ caro có các đường kẻ ngang song song và cách đều nhau.

a) Vẽ một đường thẳng d cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng MN, NP, PQ và QE.

Khám phá 3 trang 45 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

b) Vẽ một tam giác ABC rồi vẽ một đường thẳng song song với cạnh BC và cắt hai cạnh AB, AC lần lượt tại B' và C'. Trên cạnh AB, lấy đoạn AI làm đơn vị đo tính tỉ số AB' và B'B; trên cạnh AC, lấy đoạn AJ làm đơn vị đo tính tỉ số AC' và C'C (Hình 5b).

So sánh các tỉ số $\frac{A B^{'}}{A B}$ và $\frac{A C^{'}}{A C}$ ; $\frac{A B^{'}}{B' B}$ và $\frac{A C^{'}}{C' C}$ ; $\frac{B^{'} B}{AB}$ và $\frac{C^{'} C}{A C}$

Lời giải:

a) Từ hình vẽ ta thấy: độ dài các đoạn thẳng MN, NP, PQ và QE bằng nhau.

b) Từ hình vẽ ta thấy:

$\frac{A B'}{A B} = \frac{5}{7} \frac{A I}{A I} = \frac{5}{7}$ ;

$\frac{A C'}{A C} = \frac{5}{7} \frac{A J}{A J} = \frac{5}{7}$ ;

Suy ra $\frac{A B'}{A B} = \frac{A C'}{A C}$

$\frac{A B'}{B' B} = \frac{5 A I}{2 A I} = \frac{5}{2}$

$\frac{A C'}{C' C} = \frac{5 A J}{2 A J} = \frac{5}{2}$

Suy ra $\frac{A B'}{B' B} = \frac{A C'}{C' C}$

$\frac{B' B}{A B} = \frac{2 A I}{7 A I} = \frac{2}{7}$ ;

$\frac{C' C}{A C} = \frac{2 A J}{7 A J} = \frac{2}{7}$

Suy ra $\frac{B' B}{A B} = \frac{C' C}{A C}$

Giải Toán 8 trang 46 Tập 2

Thực hành 3 trang 46 Toán 8 Tập 2: Tính độ dài x, y trong Hình 8.

Thực hành 3 trang 46 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Xét tam giác ABC có d // BC, nên theo định lí Thalès, ta có:

$\frac{A E}{E B} = \frac{A F}{F C}$ $\Rightarrow$ $\frac{x}{2} = \frac{3}{1, 5}$ $\Rightarrow$ x = $\frac{3.2}{1, 5}$ = 4

Vậy x = 4.

b) Xét tam giác ABC vuông tại N, theo định lí Pythagore, ta có:

$M P^{2} = M N^{2} + N P^{2}$

$\Rightarrow M P = \sqrt{M N^{2} + N P^{2}} = \sqrt{{(5, 5 + 2, 5)}^{2} + 6^{2}} = 10$

Vì RS ⊥ MN và NP ⊥ MN suy ra RS // NP.

Xét tam giác MNP có RS // NP, nên theo định lí Thalès, ta có:

$\frac{M R}{M N} = \frac{M S}{M P} \Rightarrow \frac{5, 5}{5, 5 + 2, 5} = \frac{y}{10} \Rightarrow y = 6, 875$

Vậy y = 6,875.

Giải Toán 8 trang 48 Tập 2

Khám phá 4 trang 48 Toán 8 Tập 2: Cho tam giác ABC có AB = 6 cm, AC = 8 cm và BC = 10 cm. Lấy điểm B' trên AB sao cho AB' = 2 cm. Qua B' vẽ đường thẳng song song với BC và cắt AC tại C'.

a) Tính AC'.

b) Qua C' vẽ đường thẳng song song với AB và cắt BC tại D. Tính BD, B'C'.

c) Tính và so sánh các tỉ số: $\frac{A B'}{A B}, \frac{A C'}{A C}$ và $\frac{B' C'}{B C}$

Khám phá 4 trang 48 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Xét tam giác ABC có B'C' // BC, nên theo định lí Thalès, ta có:

$\frac{A B'}{A B} = \frac{A C'}{A C} \Rightarrow \frac{2}{6} = \frac{A C'}{8} \Rightarrow A C' = \frac{8}{3}$

Vậy AC' = $\frac{8}{3}$ .

b) Xét tam giác ABC có C'D // AB, nên theo định lí Thalès, ta có:

$\frac{B D}{B C} = \frac{A C'}{A C} \Rightarrow \frac{B D}{10} = \frac{\frac{8}{3}}{8} \Rightarrow B D = \frac{10}{3}$

Vậy BD = $\frac{10}{3}$ .

c) Ta có: $\frac{A B'}{A B} = \frac{2}{6} = \frac{1}{3}; \frac{A C'}{A C} = \frac{\frac{8}{3}}{8} = \frac{1}{3}; \frac{B' C'}{B C} = \frac{\frac{10}{3}}{10} = \frac{1}{3}$

$\Rightarrow \frac{A B'}{A B} = \frac{A C'}{A C} = \frac{B' C'}{B C} = \frac{1}{3}$

Vậy $\frac{A B'}{A B} = \frac{A C'}{A C} = \frac{B' C'}{B C}$ .

Thực hành 4 trang 48 Toán 8 Tập 2: Tìm độ dài x trên Hình 13.

Thực hành 4 trang 48 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Xét tam giác OAB có CD // AB, theo hệ quả định lí Thalès, ta có:

$\frac{C D}{A B} = \frac{O D}{O B} \Rightarrow \frac{x}{7, 8} = \frac{3, 6}{3, 6 + 1, 8} \Rightarrow x = 5, 2$

Vậy x = 5,2.

Vận dụng 2 trang 48 Toán 8 Tập 2: Với số liệu đo đạc được ghi trên Hình 14, hãy tính bề rộng CD của con kênh.

Vận dụng 2 trang 48 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Xét tam giác ACD có BE // CD, theo hệ quả định lí Thalès, ta có:

$\frac{C D}{B E} = \frac{A C}{A B} \Rightarrow \frac{C D}{3} = \frac{8 + 8}{8} \Rightarrow C D = 6 m$

Vậy bề rộng CD của con kênh là 6 m.

Khám phá 5 trang 48 Toán 8 Tập 2: Cho tam giác ABC có AB = 6cm, AC = 15 cm. Trên AB, AC lần lượt lấy B', C' sao cho AB' = 2 cm, AC' = 5 cm.

a) Tính các tỉ số $\frac{A B'}{A B}$ và $\frac{A C'}{A C}$ .

b) Qua B' vẽ đường thẳng song song với BC cắt AC tại E. Tính AE.

c) So sánh AE và AC'.

d) Hãy nhận xét về vị trí của E và C', vị trí của hai đường thẳng B'C' và B'E.

Khám phá 5 trang 48 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Ta có: $\frac{A B'}{A B} = \frac{2}{6} = \frac{1}{3};$

$\frac{A C'}{A C} = \frac{5}{15} = \frac{1}{3}$ .

b) Xét tam giác BC có B' E // BC, theo định lí Thalès, ta có:

$\frac{A B'}{A B} = \frac{A E}{A C} \Rightarrow \frac{1}{3} = \frac{A E}{15} \Rightarrow$ AE = 5cm

Vậy AE = 5 cm.

c) Ta thấy: AE = AC' = 5 cm.

d) Vì E và C' cùng thuộc AC và AE = AC' suy ra E và C' trùng nhau, B'C' và B'E trùng nhau.

Giải Toán 8 trang 49 Tập 2

Thực hành 5 trang 49 Toán 8 Tập 2: Hãy chỉ ra các cặp đường thẳng song song với nhau trong mỗi hình dưới đây.

Thực hành 5 trang 49 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Ta có: $\frac{A M}{M B} = \frac{1}{2}$ và $\frac{A N}{N C} = \frac{2}{4} = \frac{1}{2}$ , suy ra $\frac{A M}{M B} = \frac{A N}{N C}$

Theo định lí Thalès đảo trong tam giác ABC, ta có: MN // BC.

b) Ta có: $\frac{O A'}{A' A} = \frac{2}{3}$ và $\frac{O B}{B' B} = \frac{3}{4, 5} = \frac{2}{3}$ , suy ra $\frac{O A}{A' A} = \frac{O B}{B' B}$

Theo định lí Thalès đảo trong tam giác ABC, ta có: A'B' // AB.

Lại có: $\hat{B'' A'' O}$ = $\hat{O A' B'}$ mà hai góc ở vị trí so le trong suy ra A''B'' // A'B'.

Vận dụng 3 trang 49 Toán 8 Tập 2: Đo chiều cao AB của một tòa nhà bằng hai cây cọc FE, DK, một sợi dây và một thước cuộn như sau:

- Đặt cọc FE cố định, di chuyển cọc DK sao cho nhìn thấy K, F, A thẳng hàng.

- Căng thẳng dây FC đi qua K và cắt mặt đất tại C.

- Đo khoảng cách BC và DC trên mặt đất.

Cho biết DK = 1 m, BC = 24 m, DC = 1,2 m. Tính chiều cao AB của tòa nhà.

Vận dụng 3 trang 49 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Xét tam giác ABC có $A B ⊥ B C$ và $D K ⊥ A B$ nên suy ra DK // AB.

Theo hệ quả định lí Thalès, ta có:

$\frac{A B}{D K} = \frac{B C}{D C} \Rightarrow \frac{A B}{1} = \frac{24}{1, 2} \Rightarrow A B = 20 m$

Vậy chiều cao AB của tòa nhà là 20 m.

Bài tập

Bài 1 trang 49 Toán 8 Tập 2: a) Hãy đo chiều dài và chiều rộng cái bàn học của em và tính tỉ số giữa hai kích thước này.

b) Quãng đường từ Thành phố Hồ Chí Minh đi từ Mỹ Tho là 70 km, quãng đường từ Thành phố Hồ Chí Minh đi Cà Mau là 350 km. Tính tỉ số giữa hai quãng đường này.

c) Cho biết $\frac{A B}{C D} = \frac{3}{5}$ và AB = 6 cm. Hãy tính CD.

Lời giải:

a) Học sinh thực hành đo bàn học của mình và tính toán.

Ví dụ: Đo được chiều dài: 140 cm; chiều rộng: 60 cm.

Tỉ số giữa hai kích thước này: $\frac{C D}{C R} = \frac{140}{60} = \frac{7}{3}$

b) Tỉ số giữa hai quãng đường từ Thành phố Hồ Chí Minh đi từ Mỹ Tho và quãng đường từ Thành phố Hồ Chí Minh đi Cà Mau là: $\frac{70}{350} = \frac{1}{5}$

c) Ta có: $\frac{A B}{C D} = \frac{3}{5} \Rightarrow \frac{6}{C D} = \frac{3}{5} \Rightarrow C D = 10 c m .$

Vậy CD = 10 cm.

Bài 2 trang 49 Toán 8 Tập 2: Tìm x trong Hình 20.

Bài 2 trang 49 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Xét tam giác ABC có MN // BC, theo định lí Thalès, ta có:

$\frac{A M}{M B} = \frac{A N}{N C} \Rightarrow \frac{x}{2} = \frac{4, 5}{3} \Rightarrow x = 3$

Vậy x = 3.

b) Xét tam giác CDE có AB // DE, theo định lí Thalès, ta có:

$\frac{C A}{C D} = \frac{C B}{C E} \Rightarrow \frac{3}{3 + 6} = \frac{2, 4}{x} \Rightarrow x = 7, 2$

Vậy x = 7,2.

c) Xét tam giác MNP có DE ⊥ MP và MN ⊥ MP nên suy ra DE // MN.

Theo định lí Thalès, ta có:

$\frac{P M}{D M} = \frac{P N}{E N} \Rightarrow \frac{5}{x} = \frac{3, 9 + 2, 6}{2, 6} \Rightarrow x = 2$

Vậy x = 2.

Giải Toán 8 trang 50 Tập 2

Bài 3 trang 50 Toán 8 Tập 2: Với số liệu được ghi trên Hình 21. Hãy tính khoẳng cách CD từ con tàu đến trạm quan trắc đặt tại điểm C.

Bài 3 trang 50 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Ta có: $\hat{A C D} = \hat{A B E}$ mà hai góc ở vị trí đồng vị nên CD // BE.

Theo hệ quả định lí Thalès, ta có:

$\frac{C D}{B E} = \frac{A C}{A B} \Rightarrow \frac{C D}{120} = \frac{400 + 200}{200} \Rightarrow C D = 36 m$

Vậy khoảng cách từ con tàu đến trạm quan trắc là 360 m.

Bài 4 trang 50 Toán 8 Tập 2: Quan sát Hình 22, chứng minh rằng MN // BC.

Bài 4 trang 50 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Ta có: $\frac{A M}{M B} = \frac{3, 6}{2, 4} = \frac{3}{2}; \frac{A N}{N C} = \frac{4, 5}{3} = \frac{3}{2}$ .

Suy ra $\frac{A M}{M B} = \frac{A N}{N C}$ .

Theo định lí Thalès đảo, ta có: MN // BC.

Bài 5 trang 50 Toán 8 Tập 2: Tính các độ dài x, y trong Hình 23.

Bài 5 trang 50 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Xét tam giác ABC có HK // BC, theo hệ quả định lí Thalès, ta có:

$\frac{H K}{B C} = \frac{A K}{A C} \Rightarrow \frac{x}{6} = \frac{3}{3 + 1, 5} \Rightarrow x = 4$

Vậy x = 4.

b) Xét tam giác MNH có PQ // NH, theo hệ quả định lí Thalès, ta có:

$\frac{M Q}{M H} = \frac{P Q}{N H} \Rightarrow \frac{x}{x + 1, 8} = \frac{3, 8}{6, 4} \Rightarrow x = \frac{171}{65}$

Vậy $x = \frac{171}{65}$

c) Ta có: DE ⊥ AD; AB ⊥ AD suy ra DE // AB.

Theo hệ quả định lí Thalès, ta có:

$\frac{C D}{C A} = \frac{C E}{C B} = \frac{D E}{A B} \Rightarrow \frac{6}{5} = \frac{\sqrt{8^{2} + 6^{2}}}{y} = \frac{8}{x} \Rightarrow x = \frac{20}{3}; y = \frac{25}{3}$

Vậy $x = \frac{20}{3}; y = \frac{25}{3}$ .

Bài 6 trang 50 Toán 8 Tập 2: Quan sát Hình 24, chỉ ra các cặp đường thẳng song song và chứng minh điều ấy.

Bài 6 trang 50 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Ta có: $\frac{M I}{I N} = \frac{M J}{J P} = 1$ , theo định lí Thalès đảo ta có: IJ // NP.

Tương tự, ta có: $\frac{M J}{I N} = \frac{N K}{K P}$ suy ra JK // MN.

$\frac{M I}{I N} = \frac{K P}{N K}$ suy ra IK // MP.

b) Ta có: $\frac{A M}{M B} = \frac{2}{5}; \frac{A N}{A C} = \frac{3}{7, 5} = \frac{2}{5}$ suy ra $\frac{A M}{M B} = \frac{A N}{A C}$

Theo định lí Thalès đảo ta có: MN // BC.

Giải Toán 8 trang 51 Tập 2

Bài 7 trang 51 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Chứng minh rằng: OA.OD = OB.OC.

Lời giải:

Bài 7 trang 51 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

ABCD là hình thang suy ra AB // CD.

Áp dụng hệ quả định lí Thalès, ta có:

$\frac{O A}{O C} = \frac{O B}{O D} \Rightarrow O A . O D = O B . O C$ (đpcm).

Bài 8 trang 51 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Đường thẳng song song với AB cắt AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. Chứng minh rằng MN = PQ.

Lời giải:

Bài 8 trang 51 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Trong tam giác ADB, ta có: MN // AB (gt)

Suy ra $\frac{D N}{D B} = \frac{M N}{A B}$ (hệ quả định lí Thalès) (1)

Trong tam giác ACB, ta có: PQ // AB (gt)

Suy ra $\frac{C Q}{C B} = \frac{P Q}{A B}$ (hệ quả định lí Thalès) (2)

Lại có: NQ // AB (gt)

AB // CD (gt)

Suy ra NQ // CD

Trong tam giác BDC, ta có: NQ // CD (chứng minh trên)

Suy ra $\frac{D N}{D B} = \frac{C Q}{C B}$ (định lí Thalès) (3)

Từ (1), (2) và (3) suy ra $\frac{M N}{A B} = \frac{P Q}{A B}$ hay MN = PQ (đpcm).

Bài 9 trang 51 Toán 8 Tập 2: Quan sát Hình 25 và chứng minh $x = \frac{a h}{a' - a}$ .

Bài 9 trang 51 Toán 8 Tập 2 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Xét tam giác ABC có BC ⊥ AB' và B'C'⊥ AB' nên suy ra BC // B'C'.

Theo hệ quả định lí Thalès, ta có:

$\frac{A B}{A B'} = \frac{B C}{B C'} \Rightarrow \frac{x}{x + h} = \frac{a}{a'}$

$\Rightarrow a' x = a (x + h) \Rightarrow a' x - a x = a h$

$\Rightarrow x (a' - a) = a h \Rightarrow x = \frac{a h}{a' - a}$ (đpcm).

Lý thuyết Định lí Thalès trong tam giác

1. Tỉ số của hai đoạn thẳng

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là:

Chú ý:

- Để tính tỉ số của hai đoạn thẳng, ta phải đưa chúng về cùng một đơn vị đo.

- Tỉ số của hai đoạn thẳng đó không phụ thuộc vào đơn vị đo độ dài đoạn thẳng.

Đoạn thẳng tỉ lệ

Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức: hay

2. Định lí Thalès

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.

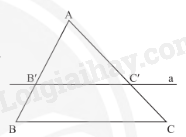
Lý thuyết Định lí Thalès trong tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

3. Hệ quả của định lí Thalès

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

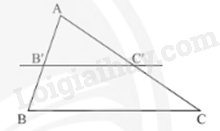
Lý thuyết Định lí Thalès trong tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 2)

4. Định lí Thalès đảo

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Lý thuyết Định lí Thalès trong tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 3)