Với giải sách bài tập Toán 8 Bài 2: Tọa độ của một điểm và đồ thị của hàm số sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 2: Tọa độ của một điểm và đồ thị của hàm số
Bài 1 trang 10 SBT Toán 8 Tập 2: Tìm toạ độ của các điểm A, B, C, D, E trong Hình 8.
Lời giải:
Dựa vào mặt phẳng toạ độ Oxy ở Hình 8, ta xác định được toạ độ các điểm là:
A(0; 2), B(2; 3), C(1; 0), D(–3; 1), E(4; –2).
Vậy toạ độ các điểm là A(0; 2), B(2; 3), C(1; 0), D(–3; 1), E(4; –2).
Lời giải:
Vẽ mặt phẳng toạ độ Oxy và xác định các điểm A(1; 2), B(4; 2), C(4; 5) trên mặt phẳng
Để ABCD là hình vuông thì AD AB và AD = AB = BC = CD = 3.
Do đó xác định được điểm D trên mặt phẳng toạ độ Oxy là D(1; 5).
Vậy toạ độ đỉnh D là D(1; 5).
Bài 3 trang 10 SBT Toán 8 Tập 2: Xác định toạ độ của các điểm sau:
a) Điểm M nằm trên trục tung và có tung độ là 3.
b) Điểm N nằm trên trục hoành và có hoành độ là –6.
c) Điểm O là gốc toạ độ.
Lời giải:
a) Điểm M nằm trên trục tung nên hoành độ xM = 0.
Điểm M có tung độ là 3 hay yM = 3.
Vậy toạ độ điểm M là M(0; 3).
b) Điểm N nằm trên trục hoành nên tung độ yM = 0.
Điểm N có hoành độ là –6 hay xM = –6.
Vậy toạ độ điểm N là M(–6; 0).
c) Điểm O là gốc toạ độ nên có toạ độ là O(0; 0).
Lời giải:
Ta vẽ hệ trục toạ độ Oxy và đánh dấu các điểm A(2; 3), B(2; –1), C(–3; 3).
Dựa vào mặt phẳng toạ độ ta thấy AB AC nên tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
SABC = AB.AC = .4.5 = 10 (đvdt)
Bài 5 trang 10 SBT Toán 8 Tập 2: a) Tìm toạ độ các điểm M, N, P, Q trong Hình 9.
b) Em có nhận xét gì về vai trò của tia phân giác của góc so với hai đường thẳng MN, PQ?
Lời giải:
a) Dựa vào mặt phẳng toạ độ Oxy trong Hình 9 ta xác định được toạ độ các điểm là:
M(3; 2), N(2; 3), P(–2; 0) và Q(0; –2).
b) Các đoạn thẳng MN và PQ đều nhận tia phân giác của góc làm trục đối xứng.
Bài 6 trang 10 SBT Toán 8 Tập 2: Tìm toạ độ các điểm A, B, C, D, E và F trong Hình 10.
Lời giải:
Dựa vào mặt phẳng toạ độ Oxy trong Hinhg 10 ta xác định được toạ độ các điểm là:
A(–4; 3), B(0; 3), C(–1; 0), D(–3; –3), E(1; –2) và F(3; 1).
Vậy toạ độ các điểm là A(–4; 3), B(0; 3), C(–1; 0), D(–3; –3), E(1; –2) và F(3; 1).
Lời giải:
Trên mặt phẳng toạ độ Oxy, ta xác định toạ độ các điểm:
A(3; –1), B(2; 5), C(4; 1) và D(–4; –4).
Để trục hoành là đường trung trực của AA’, BB’, CC’ và DD’ thì các điểm A’, B’, C’ và D’ phải đối xứng với A, B, C và D qua trục hoành
Do đó A’(3;1), B’(2; –5), C’(4; –1) và D’(–4; 4).
Vậy toạ độ các điểm cần tìm là A’(3; 1), B’(2; –5), C’(4; –1) và D’(– 4; 4).
Lời giải:
Trên mặt phẳng toạ độ Oxy, ta xác định toạ độ các điểm:A(0; 5) và B(–3; 5).
Dựa vào mặt phẳng toạ độ Oxy ta thấy rằng tất cả các điểm nằm trên đường thẳng AB đều có tung độ bằng 5.
Lời giải:
Ta có:y = g(x) = x2 – 1.
•Thay x = –3 vào g(x) ta được: g(–3) = ( –3)2 – 1 = 8.
Do đó A(–3; 8) thuộc đồ thị hàm số y = x2 – 1.
•Thay x = –2 vào g(x) ta được: g(–2) = (–2)2 – 1 = 3 5
Do đó B(–2; 5) không thuộc đồ thị hàm số y = x2 – 1.
•Thay x = vào g(x) ta được: .
Do đó không thuộc đồ thị hàm số y = x2 – 1
Vậy A(–3; 8), C(1; 0) thuộc đồ thị hàm số y = x2 – 1.
B(–2; 5), không thuộc đồ thị hàm số y = x2 – 1.
Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tọa độ của một điểm và đồ thị của hàm số
Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
Bài 1: Phương trình bậc nhất một ẩn
Lý thuyết Tọa độ của một điểm và đồ thị của hàm số
1. Tọa độ của một điểm
a. Khái niệm:
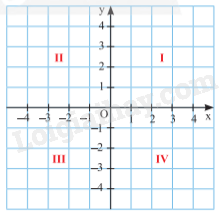
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.
Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: góc phần tư thứ I, II, III, IV.
b. Tọa độ của một điểm:
Trong mặt phẳng tọa độ, mỗi điểm P xác định duy nhất một cặp số (a; b) và mỗi cặp số (a; b) xác định duy nhất một điểm M.
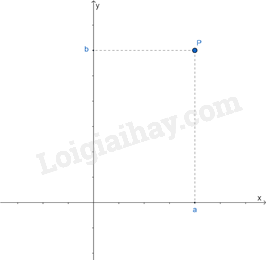
Cặp số (a; b) gọi là tọa độ của M, kí hiệu là M(a; b), trong đó a là hoành độ, b là tung độ của điểm M.
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.
2. Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó
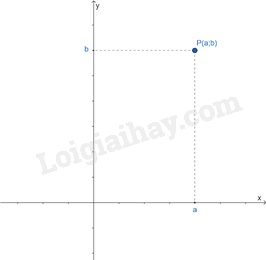
Để xác định một điểm điểm P có tọa độ là (a; b), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục này tại điểm a.
- Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này tại điểm b.
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm.
Chú ý: Trên mặt phẳng tọa độ, mỗi cặp số (a; b) xác định một điểm P duy nhất.
Ví dụ: Biểu diễn điểm M(2; -3) trên mặt phẳng tọa độ Oxy
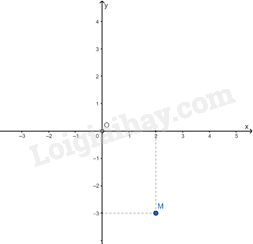
3. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M(x; f(x)).
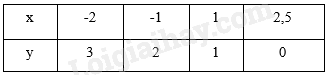
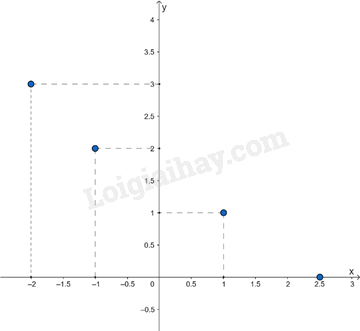
Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng: