Với giải sách bài tập Toán 8 Bài 4: Hệ số góc của đường thẳng sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 4: Hệ số góc của đường thẳng
Bài 1 trang 17 SBT Toán 8 Tập 2: Cho hàm số y = ax + 2. Tìm hệ số góc a, biết rằng:
a) Đồ thị của hàm số đi qua điểm A(1; 3).
b) Đồ thị của hàm số song song với đường thằng y = –2x + 1.
Lời giải:
a) Vì đồ thị hàm số y = ax + 2 đi qua điểm A(1; 3) nên 3 = a.1 + 2 a = 1.
Vậy a = 1.
b) Vì đồ thị của hàm số y = ax + 2 song song với đường thằng y = –2x + 1 nên
Vậy a = –2.
a) Hai đường thẳng song song với nhau?
b) Hai đường thẳng cắt nhau?
Lời giải:
a) Để đường thẳng y = 2mx + 11 song song với đường thằng y = (1 – m)x + 2 thì:
Vậy m = .
b) Để đường thẳng y = 2mx + 11 cắt đường thằng y = (1 – m)x + 2 thì:
2m 1 – m
3m 1 m
Vậy m.
Bài 3 trang 17 SBT Toán 8 Tập 2: Cho hàm số y = 2x + b. Tìm b trong mỗi trường hợp sau:
a) Với x = 4 thì hàm số có giá trị bằng 5.
b) Đồ thị của hàm số đã cho cắt trục tung tại điểm có tung độ bằng 7.
c) Đồ thị của hàm số đã cho đi qua điểm A(1; 5).
Lời giải:
a) Với x = 4 thì hàm số có giá trị bằng 5 nên thay vào hàm số y = 2x + b ta có:
5 = 2.4 + b b = 5 – 8 = –3.
Vậy b = –3.
b) Vì đồ thị của hàm số y = 2x + b cắt trục tung tại điểm M có tung độ bằng 7 nên toạ độ điểm M(0; 7).
Thay M(0; 7) vào y = 2x + b ta được:
2.0 + b = 7 b = 7.
Vậy b = 7.
c) Đồ thị của hàm số y = 2x + b đi qua điểm A(1; 5).
Thay A(1; 5) vào y = 2x + b ta được:
2.1 + b = 5 b = 5 – 2 = 3
Vậy b = 3.
a) Đồ thị của hàm số đã cho đi qua điểm A(3; 4).
b) Đồ thị của hàm số là đường thẳng có hệ số góc bằng .
c) Đồ thị của hàm số là đường thẳng song song với đường thẳng d2: y = –6x – 5.
Lời giải:
a) Đồ thị của hàm số y = ax + b là đường thằng d1 đi qua gốc toạ độ nên 0 = a.0 + b.
Do đó b = 0.
Đồ thị hàm số có dạng: y = ax.
Đồ thị y = ax đi qua điểm A(3; 4) thay A(3; 4) vào đồ thị ta được:
4 = 3a a = .
Vậy hàm số cần tìm có phương trình y = x.
b) Đồ thị của hàm số y = ax có hệ số góc bằng hay a = .
Vậy hàm số cần tìm có phương trình y = x.
c) Vì đồ thị của hàm số y = ax song song với đường thẳng d2: y = –6x – 5 nên a = –6.
Vậy hàm số cần tìm có phương trình y = –6x.
a) A(1; 5) và B(0; 2).
b) M(1; 9) và N(0; 1).
c) P(0; 2) và Q(1; 0).
Lời giải:
a) Đồ thị của hàm số y = ax + b đi qua điểm A(1; 5) và B(0; 2).
Thay A(1; 5) và B(0; 2) vào hàm số ta có hệ phương trình:
Vậy hàm số cần tìm có phương trình y = 3x + 2.
b) Đồ thị của hàm số y = ax + b đi qua điểm M(1; 9) và N(0; 1).
Thay M(1; 9) và N(0; 1) vào hàm số ta có hệ phương trình:
Vậy hàm số cần tìm có phương trình y = 8x + 1.
c) Đồ thị của hàm số y = ax + b đi qua điểm P(0; 2) và Q(1; 0).
Thay P(0; 2) và Q(1; 0) vào hàm số ta có hệ phương trình:
Vậy hàm số cần tìm có phương trình y = –2x + 2.
Bài 6 trang 17 SBT Toán 8 Tập 2: Hãy xác định hàm số y = ax + b trong mỗi trường hợp sau:
a) Đồ thị của hàm số là đường thẳng đi qua điểm B(–1; 2) và cắt trục tung tại điểm có tung độ bằng 3.
b) Đồ thị của hàm số là đường thẳng song song với đường thẳng y = –3x + 1 và cắt trục hoành tại điểm có hoành độ bằng 3.
c) Đồ thị của hàm số là đường thẳng cắt trục tung tại điểm có tung độ bằng –6 và cắt trục hoành tại điểm có hoành độ bằng 2.
Lời giải:
a) Đồ thị của hàm số y = ax + b đi qua điểm B(–1; 2).
•Thay B(–1; 2) vào y = ax + b, ta được:
2 = –1.a + b b – a = 2 (1)
Đồ thị của hàm số y = ax + b cắt trục tung tại điểm M có tung độ bằng 3 hay M(0; 3).
•Thay M(0; 3) vào y = ax + b, ta được:
3 = a.0 + b b = 3
•Thay b = 3 vào (1) ta có:
3 – a = 2 a = 1
Vậy hàm số cần tìm có phương trình y = x + 3.
b) Đồ thị của hàm số y = ax + b song song với đường thẳng y = –3x + 1 nên
Đồ thị của hàm số y = ax + b cắt trục hoành tại điểm N có hoành độ bằng 3 nên N(3; 0).
•Thay N(3; 0) vào y = ax + b ta được: 3a + b = 0.
•Thay a = –3 vào ta có: 3.(–3) + b = 0 b = 9 (TMĐK).
Vậy hàm số cần tìm có phương trình y = –3x + 9.
c) Đồ thị của hàm số y = ax + b cắt trục tung tại điểm P có tung độ bằng – 6 hay P(0; –6).
Thay P(0; –6) vào y = ax + b ta được: 3.0 + b = –6 b = –6.
Đồ thị của hàm số y = ax + b cắt trục hoành tại điểm Q có hoành độ bằng 2 hay Q(2; 0).
Thay Q(2; 0) vào y = ax + b ta được: 2a + b = 0.
Mà b = –6 nên 2a – 6 = 0 a = 3.
Vậy hàm số cần tìm có phương trình y = 3x – 6.
Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Phương trình bậc nhất một ẩn
Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất
Lý thuyết Hệ số góc của đường thẳng
1. Hệ số góc của đường thẳng
Góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.
Góc tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc )
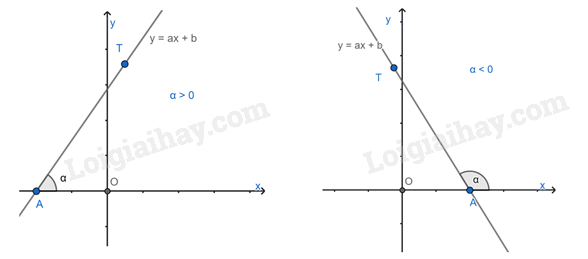
Hệ số góc: Ta gọi a là hệ số góc của đường thẳng y = ax + b (a0).
Ví dụ: Đường thẳng y = 3x – 1 có hệ số góc là 3;
y = 2 – x có hệ số góc là -1.
2. Hai đường thẳng song song, hai đường thẳng cắt nhau
Hai đường thẳng y = ax + b (a0) và y = a’x + b’ (a’0) song song với nhau khi a = a’; b b’ và ngược lại.
Hai đường thẳng y = ax + b (a0) và y = a’x + b’ (a’0) trùng nhau khi a = a’; b = b’ và ngược lại.
Hai đường thẳng y = ax + b (a0) và y = a’x + b’ (a’0) cắt nhau khi a a’ và ngược lại.
Ví dụ: Đường thẳng y = -x + 1 và đường thẳng y = -x song song với nhau.
Đường thẳng y = -x + 1 và đường thẳng y = 2x + 1 cắt nhau.