Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 2: Tọa độ của một điểm và đồ thị của hàm số chi tiết sách Toán 8 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 2: Tọa độ của một điểm và đồ thị của hàm số
Khởi động trang 10 Toán 8 Tập 2: Bạn Cúc mới học chơi cờ vua. Em hãy tìm giúp bạn:
- Quân Hậu Trắng đang ở giao của các cột nào của hàng nào?
- Tại giao của cột b và hàng 8 là quân gì? Cho biết tên gọi của các quân cờ trên bàn cờ vua như sau:
Lời giải:
- Quân Hậu Trắng đang ở giao của cột d và hàng 1.
- Tại giao của cột b và hàng 8 là quân mã đen.
1. Tọa độ của một điểm
Lời giải:
Con tàu ở vị trí A cách trục Ox 8 km và cách trục Oy 4 km;
Hòn đảo ở vị trí B cách trục Ox 7 km và cách trục Oy 3 km.
Thực hành 1 trang 11 Toán 8 Tập 2: Tìm tọa độ của các điểm O, E, F trong Hình 4.
Lời giải:
Qua E kẻ các đường thẳng vuông góc với hai trục tọa độ, các đường này cắt Ox tại điểm −3 và cắt Oy tại điểm 4. Ta được tọa độ điểm E là (−3; 4).
Qua O kẻ các đường thẳng vuông góc với hai trục tọa độ, các đường này cắt Ox tại điểm 0 và cắt Oy tại điểm 0. Ta được tọa độ điểm O là (0; 0).
Qua F kẻ các đường thẳng vuông góc với hai trục tọa độ, các đường này cắt Ox tại điểm 5 và cắt Oy tại điểm −3. Ta được tọa độ điểm E là (5; −3).
Lời giải:
Qua A kẻ các đường thẳng vuông góc với hai trục tọa độ, các đường này cắt Ox tại 4 và cắt Oy tại 8. Ta được tọa độ A của con thuyền là (4; 8).
Qua B kẻ các đường thẳng vuông góc với hai trục tọa độ, các đường này cắt Ox tại −3 và cắt Oy tại 7. Ta được tọa độ A của con thuyền là (−3; 7).
2. Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó
Lời giải:
Kẻ một đường thẳng vuông góc với Ox tại điểm 6 và một đường thẳng vuông góc với Oy tại điểm 4, hai đường thẳng này cắt nhau tại A có tọa độ (6;4).
Lời giải:
Các điểm C(3; 0), D(0; 2), E(−3; −4) được xác định trên mặt phẳng tọa độ Oxy như sau:
Lời giải:
Học sinh tự thực hành trên bản đồ Việt Nam.
3. Đồ thị của hàm số
Khám phá 3 trang 12 Toán 8 Tập 2: Làm thế nào để biểu diễn hàm số y = f(x) trên mặt phẳng tọa độ?
Lời giải:
Người ta có thể biểu diễn hàm số y = f(x) một cách trực quan bằng cách vẽ các điểm có tọa độ (x; y) trong mặt phẳng tọa độ.
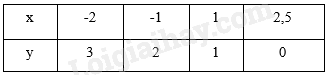
Thực hành 3 trang 13 Toán 8 Tập 2: Vẽ đồ thị của hàm số y = f(x) cho bằng bảng sau:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y |
2 |
1 |
0 |
−1 |
−2 |
Lời giải:
Đồ thị hàm số là tập hợp các điểm có tọa độ A(−2; 2), B(−1; 1), O(0; 0), D(1; −1), E(2; −2) được vẽ trên mặt phẳng tọa độ sau:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y |
? |
? |
? |
? |
? |
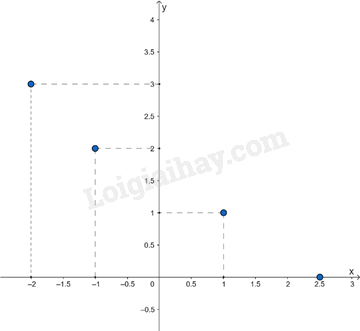
Lời giải:
Ta có bảng giá trị của hàm số có đồ thị đã cho như sau:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y |
4 |
1 |
0 |
1 |
4 |
Bài tập
Bài 1 trang 14 Toán 8 Tập 2: Vẽ một trục tọa độ Oxy và đánh dấu các điểm A(−2; 0), B(3; 0), C(4; 0).
a) Em có nhận xét gì về các điểm A, B, C?
b) Em hãy cho biết một điểm bất kì trên trục hoành có tung độ bằng bao nhiêu.
Lời giải:
a) Xác định được các điểm A(−2; 0), B(3; 0), C(4; 0) trên hệ trục tọa độ Oxy như sau:
Nhận xét: các điểm A(−2; 0), B(3; 0), C(4; 0) đều nằm trên trục hoành và có tung độ bằng 0.
b) Bất kì một điểm nằm trên trục hoành đều có tung độ bằng 0.
a) Em có nhận xét gì về các điểm M, N, P?
b) Em hãy cho biết một điểm bất kì trên trục tung có hoành độ bằng bao nhiêu?
Lời giải:
Xác định được các điểm M(0; −2), N(0; 1), P(0; 4) trên hệ trục tọa độ Oxy như sau:
Nhận xét ba điểm M, N, P cùng nằm trên trục tung.
b) Một điểm bất kì trên trục tung có hoành độ bằng 0.
Lời giải:
Tứ giác ABCD là hình vuông.
Bài 4 trang 14 Toán 8 Tập 2: Vẽ đồ thị hàm số được cho bởi bảng sau:
|
x |
−3 |
−1 |
0 |
1 |
2 |
|
y |
−6 |
−2 |
0 |
2 |
4 |
Lời giải:
Đồ thị hàm số là tập hợp các điểm có tọa độ (−3; −6), (−1; −2), (1; 2), (2; 4) được vẽ trên mặt phẳng tọa độ như sau:
Bài 5 trang 14 Toán 8 Tập 2: Trong những điểm sau, tìm điểm thuộc đồ thị của hàm số y = 4x:
M(−1; −4); M(1; −4); .
Lời giải:
• Thay tọa độ điểm M vào hàm số ta có −4 = 4.( −1) suy ra M thuộc đồ thị hàm số y = 4x.
• Thay tọa độ điểm N vào hàm số ta có −4 ≠ 4.1 suy ra N không thuộc đồ thị hàm số
y = 4x.
• Thay tọa độ điểm P vào hàm số ta có suy ra P thuộc đồ thị hàm số y = 4x.
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y |
−6 |
−3 |
0 |
3 |
6 |
a) Vẽ một hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị (x; y) tương ứng có trong bảng trên?
b) Em có nhận xét gì các điểm vừa xác định trong câu a?
Lời giải:
a)
b) 5 điểm trên là các điểm thẳng hàng.
a) Tìm tọa độ các điểm H, D, M.
b) Hỏi ai mua nhiều quyển vở nhất?
Lời giải:
a) H(3;9); D(4;12); M(2;6)
b) Trục tung biểu thị cho số quyển vở x của ba bạn, do đó bạn Dũng mua nhiều vở nhất (x = 4)
|
t |
18 |
20 |
21 |
25 |
28 |
30 |
|
S |
36 |
40 |
42 |
50 |
56 |
60 |
Vẽ đồ thị của hàm số S theo biến số t.
Lời giải:
Lý thuyết Tọa độ của một điểm và đồ thị của hàm số
1. Tọa độ của một điểm
a. Khái niệm:
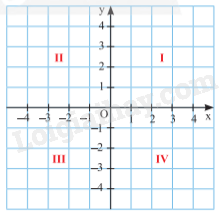
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.
Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: góc phần tư thứ I, II, III, IV.
b. Tọa độ của một điểm:
Trong mặt phẳng tọa độ, mỗi điểm P xác định duy nhất một cặp số (a; b) và mỗi cặp số (a; b) xác định duy nhất một điểm M.
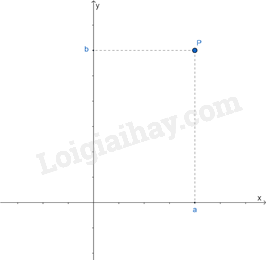
Cặp số (a; b) gọi là tọa độ của M, kí hiệu là M(a; b), trong đó a là hoành độ, b là tung độ của điểm M.
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.
2. Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó
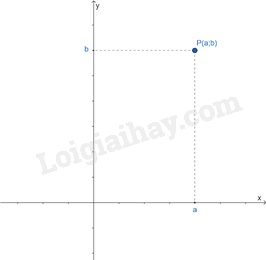
Để xác định một điểm điểm P có tọa độ là (a; b), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục này tại điểm a.
- Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này tại điểm b.
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm.
Chú ý: Trên mặt phẳng tọa độ, mỗi cặp số (a; b) xác định một điểm P duy nhất.
Ví dụ: Biểu diễn điểm M(2; -3) trên mặt phẳng tọa độ Oxy
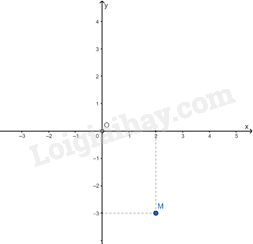
3. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M(x; f(x)).
Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
