Với lời giải Toán 11 trang 72 Tập 1 chi tiết trong Bài 2: Giới hạn của hàm số sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 Bài 2: Giới hạn của hàm số
Thực hành 1 trang 72 Toán 11 Tập 1: Tìm các giới hạn sau:
a) ;
b) .
Lời giải:
a) Hàm số f(x) = 2x2 – x xác định trên ℝ.
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ∈ ℝ với mọi n và xn → 3 khi n → +∞. Ta có: .
Vậy .
b) Hàm số xác định trên tập ℝ\{– 1}.
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ∈ ℝ\{– 1} với mọi n và xn → – 1 khi n → +∞.
Ta có:
Vậy .
2. Các phép toán về giới hạn hữu hạn của hàm số
Hoạt động khám phá 2 trang 72 Toán 11 Tập 1: Cho hai hàm số y = f(x) = 2x và y = g(x) = .
a) Giả sử (xn) là dãy số bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞. Tìm giới hạn lim[f(xn) + g(xn)].
b) Từ đó, tìm giới hạn , và so sánh với .
Lời giải:
+) Hàm số y = f(x) = 2x xác định trên .
Dãy số (xn) bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞, ta có:
limf(xn) = lim(2xn) = 2.limxn = 2.1 = 2.
Suy ra = 2.
+) Hàm số y = g(x) = xác định trên ℝ \ {2}.
Dãy số (xn) bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞, ta có:
limg(xn) =.
Suy ra .
a) Ta có: lim[f(xn) + g(xn)] = limf(xn) + limg(xn) = .
b) Ta có nên .
Ta lại có: .
Vì vậy .
Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 72 Toán 11 Tập 1: Tìm các giới hạn sau:....
Hoạt động khám phá 2 trang 72 Toán 11 Tập 1: Cho hai hàm số y = f(x) = 2x và y = g(x) = .....
Thực hành 2 trang 73 Toán 11 Tập 1: Tìm các giới hạn sau:.....
Thực hành 3 trang 75 Toán 11 Tập 1: Cho hàm số 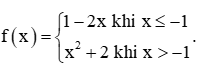
Hoạt động khám phá 4 trang 75 Toán 11 Tập 1: Cho hàm số có đồ thị như Hình 3....
Thực hành 4 trang 76 Toán 11 Tập 1: Tìm các giới hạn sau:....
Hoạt động khám phá 5 trang 77 Toán 11 Tập 1: Cho hàm số có đồ thị như Hình 4....
Thực hành 5 trang 78 Toán 11 Tập 1: Tìm các giới hạn sau....
Bài 1 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:....
Bài 2 trang 79 Toán 11 Tập 1: Cho hàm số 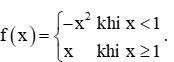
Bài 3 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:....
Bài 4 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:...
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: