Với giải sách bài tập Toán 11 Bài 3: Đường thẳng và mặt phẳng song song sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 3: Đường thẳng và mặt phẳng song song
Lời giải:
Gọi M, N lần lượt là trung điểm của DB, DC.
Xét ∆DBC có M, N lần lượt là trung điểm của DB, DC nên MN là đường trung bình của ∆DBC, suy ra MN // BC.
Do G1 là trọng tâm ∆ABD nên ;
G2 là trọng tâm ∆ACD nên .
Do đó .
Trong tam giác AMN, ta có nên G1G2 // MN (định lí Thalès đảo)
Mà MN // BC (chứng minh trên)
Suy ra G1G2 // MN // BC, mà BC ⊂ (ABC), MN ⊂ (BCD).
Suy ra G1G2 song song với các mặt phẳng (ABC) và (BCD).
a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho AM = AF, AN = AD Chứng minh MN // (DCEF).
Lời giải:
a) Do O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.
Xét trong ∆BDF có: O, O’ lần lượt là trung điểm của BD, BF nên OO’ là đường trung bình của ∆BDF, suy ra OO’ // DF (1)
Tương tự, trong ∆ACE ta cũng có OO’ // CE (2)
Từ (1) và (2) suy ra OO’ // DF // CE, mà DF ⊂ (ADF), CE ⊂ (BCE)
Suy ra OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Do AM = AF, AN = AD nên
Xét ∆ADF có suy ra MN // DF (định lý Thalès đảo)
Mà DF ⊂ (DCEF), suy ra MN // (DCEF).
a) NG // (SCD);
b) MG // (SCD).
Lời giải:
a) Gọi F là giao điểm của MN và BC.
Ta có MN // AB, suy ra NF // BI (vì F ∈ MN, I ∈ AB).
Trong ∆CIB có NF // BI, nên theo định lí Thalès ta có: (1)
Mặt khác, AM = AD suy ra
Lại có MF // AB // DC nên (2)
Từ (1) và (2) suy ra
Trong ∆SAB, ta có G là trọng tâm nên .
Trong ∆SIC, ta có suy ra GN // SC (định lí Thalès đảo).
Mà SC ⊂ (SDC), do đó NG // (SDC).
b) Trong mặt phẳng (ABCD), gọi O là giao điểm của MI và DC.
Trong ∆OCI có MN // OC (do O ∈ DC), suy ra (theo định lí Thalès).
Mà (G là trọng tâm của ∆SAB).
Do đó, trong ∆SOI có , suy ra MG // OS (định lí Thalès đảo).
Mà OS ⊂ (SDC), do đó MG // (SDC).
a) MN song song với các mặt phẳng (SBC) và (SAD);
b) SB song song với (MNP);
c) SC song song với (MNP).
d) Gọi G1 và G2 theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh G1G2 song song với (SAD).
Lời giải:
a) Hình bình hành ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD nên MN // AD // BC
Ta có MN // BC và BC ⊂ (SBC), suy ra MN // (SBC);
MN // AD và AD ⊂ (SAD), suy ra MN // (SAD).
Vậy MN song song với các mặt phẳng (SBC) và (SAD).
b) Trong ∆SAB, có P, M lần lượt là trung điểm của SA, AB nên PM là đường trung bình, suy ra PM // SB
Mà PM ⊂ (MNP), suy ra SB // (MNP).
c) Trong mặt phẳng (SAB) vẽ đường thẳng d đi qua S và song song AB.
Gọi E là giao điểm của MP và d.
Ta có d // AB hay ES // AB, mà AB // CD nên ES // DC, tức là ES // NC (1)
Ta cũng có ES // MB và EM // SB nên MBSE là hình bình hành, suy ra ES = MB
Mà MB = NC (do M, N lần lượt là trung điểm của AB, DC và AB = DC)
Suy ra ES = NC (2)
Từ (1) và (2) suy ra ESCN là hình bình hành nên SC // NE.
Lại có NE ⊂ (MNP), suy ra SC // (MNP).
d) Gọi I là trung điểm của BC.
Do G1 và G2 theo thứ tự là trọng tâm của ∆ABC và ∆SBC nên
Trong ∆SIA, ta có , suy ra G1G2 // SA (định lí Thalès đảo)
Mà SA ⊂ (SAD), nên G1G2 // (SAD).
Lời giải:
Gọi N, P, R lần lượt là trung điểm của AD, SD, SB.
Xét ∆ABD có M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của tam giác. Do đó MN // BD.
Xét ∆SBD có P, R lần lượt là trung điểm của SD, SB nên PR là đường trung bình của tam giác. Do đó PR // BD.
Từ các kết quả trên ta có: MN // PR (do cùng song song với BD).
Suy ra bốn điểm M, N, P, R tạo thành một mặt phẳng (MNPR).
Ta có MN // BD và MN ⊂ (MNPR) nên BD // (MNPR)
Tương tự, ta cũng có SA // (MNPR)
Ta thấy (MNPR) đi qua M và song song với BD, và SA nên chính là mp(α).
Trong mặt phẳng (SAB) vẽ đường thẳng d đi qua S và d // AB // CD.
Khi đó, giả sử MR cắt d tại I, PI cắt SC tại Q.
Lúc này, mặt phẳng (α) là (MNPI).
Ta có MN ⊂ (ABCD), MN ⊂ (MNPI) nên (MNPI) ∩ (ABCD) = MN hay (α) ∩ (ABCD) = MN.
Tương tự, (α) ∩ (SAD) = NP, (α) ∩ (SCD) = PQ, (α) ∩ (SBC) = QR, (α) ∩ (SAB) = MR.
Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Hai đường thẳng song song
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm
Lý thuyết Đường thẳng và mặt phẳng song song
1. Đường thẳng song song với mặt phẳng
- Nếu a và có một điểm chung duy nhất thì ta nói a và cắt nhau tại A. Kí hiệu hay .
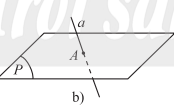
- Nếu a và có từ 2 điểm chung phân biệt trở lên thì ta nói a nằm trong hay chứa a. Kí hiệu hay .
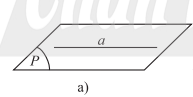
- Nếu a và không có điểm chung thì ta nói a song song với hay song song với a. Kí hiệu là hay .
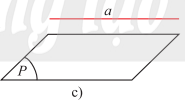
*Đường thẳng a song song với mặt phẳng (P) nếu chúng không có điểm chung.
2. Điều kiện để một đường thẳng song song với một mặt phẳng
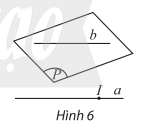
3. Tính chất cơ bản của đường thẳng và mặt phẳng song song
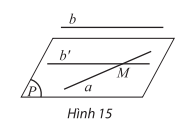
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a // b.
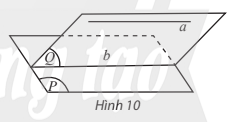
* Hệ quả:
- Cho đường thẳng a song song với mặt phẳng (P). Nếu qua điểm M thuộc (P) ta vẽ đường thẳng b song song với a thì b phải nằm trong (P).
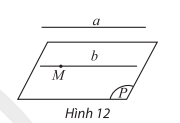
- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
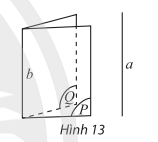
* Mặt phẳng đi qua một trong hai đường thẳng chéo nhau và song song vơi đường thẳng còn lại
- Nếu a và b là hai đường thẳng chéo nhau thì qua a, có một và chỉ một mặt phẳng song song với b.