Với lời giải SBT Toán 10 trang 69 Tập 1 chi tiết trong Bài tập cuối chương 4 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài tập cuối chương 4
Bài 4.54 trang 69 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; −1), B(–1; 5) và C(3m; 2m –1). Tất cả các giá trị của tham số m sao cho AB ⊥ OC là
A. m = –2;
B. m = 2;
C. m = ±2;
D. m = 3.
Lời giải:
Đáp án đúng là: B
Với A(2; −1), B(–1; 5) và C(3m; 2m –1) ta có:
và
Để AB ⊥ OC thì
Û −3.3m + 6.(2m – 1) = 0
Û −9m + 12m – 6 = 0
Û 3m = 6
Û m = 2.
Vậy ta chọn phương án B.
Bài 4.55 trang 69 SBT Toán 10 Tập 1: Cho tam giác ABC vuông tại A với AB = 1, AC = 2. Lấy M, N, P tương ứng thuộc các cạnh BC, CA, AB sao cho 2BM = MC, CN = 2NA, AP = 2PB. Giá trị của tích vô hướng bằng
A.
B.
C. 0;
D. 1.
Lời giải:
Đáp án đúng là: C
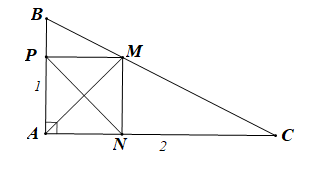
Ta có:
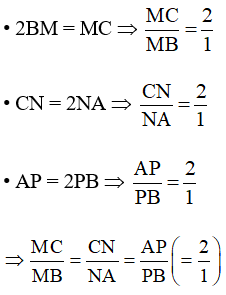
Þ MN // AB và PM // AC (định lí Talet đảo)
Þ ANMP là hình bình hành
Mặt khác:
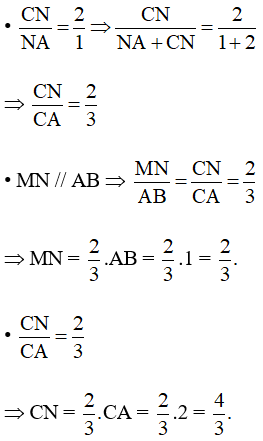
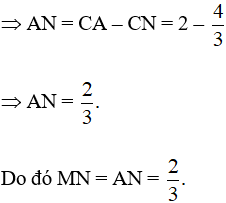
Hình bình hành ANMP có MN = AN nên là hình thoi
Khi đó hai đường chéo AM và PN vuông góc với nhau
Vậy ta chọn phương án C.
Bài 4.56 trang 69 SBT Toán 10 Tập 1: Cho tam giác ABC đều các cạnh có độ dài bằng 1. Lấy M, N, P lần lượt thuộc các cạnh BC, CA, AB sao cho BM = 2MC, CN = 2NA và AM ⊥ NP. Tỉ số của bằng
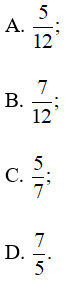
Lời giải:
Đáp án đúng là: A
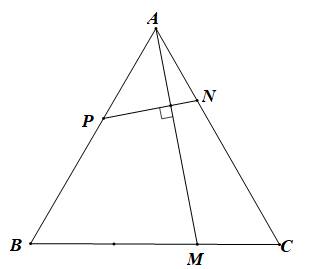
Giả sử (x > 0)
Ta có:
• Ta có: MB = 2MC nên M nằm giữa B và C
Hay
Do đó
Tương tự ta cũng có và
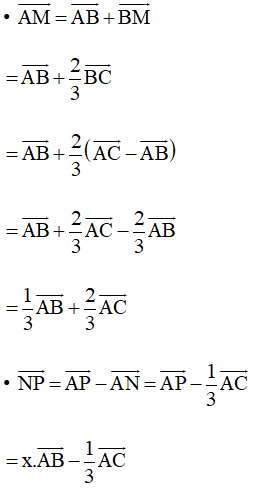
Mặt khác ta có: AM ⊥ NP
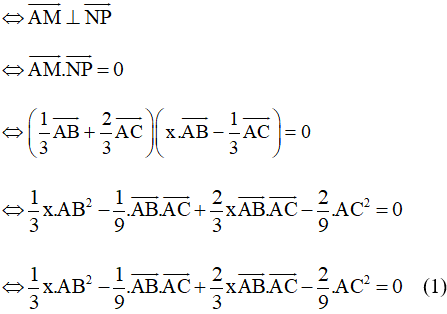
Tam giác ABC đều có độ dài cạnh bằng 1 nên AB = AC = BC = 1 và
Ta có:
= 1.1.cos60° =
Khi đó:
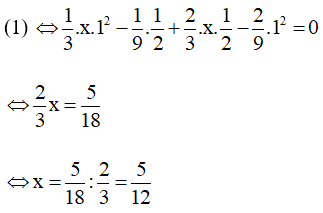
(thỏa mãn)
Vậy
Ta chọn phương án A.
Bài 4.57 trang 69 SBT Toán 10 Tập 1: Cho tam giác ABC đều có độ dài các cạnh bằng 3a. Lấy điểm M thuộc cạnh BC sao cho MB = 2MC. Tích vô hướng của hai vectơ và bằng
A.
B.
C. a2;
D. –a2.
Lời giải:
Đáp án đúng là: B
Ta có: MB = 2MC nên M nằm giữa B và C
Hay
Do đó
Tương tự ta có
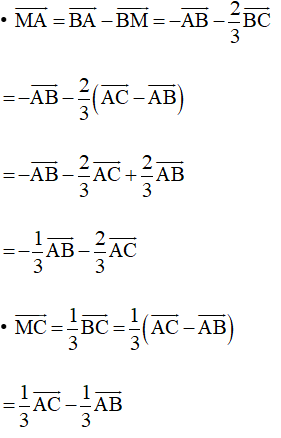
• Khi đó:
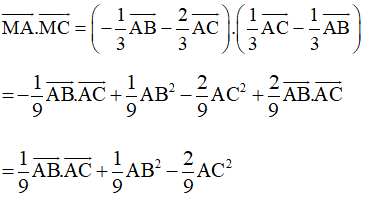
• Tam giác ABC đều có độ dài cạnh bằng 3a nên AB = AC = BC = 3a và
Ta có:
= 3a.3a.cos60° =
Do đó
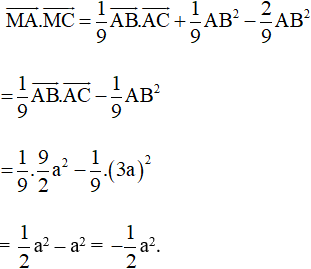
Vậy a2.
Ta chọn phương án B.
Bài 4.58 trang 69 SBT Toán 10 Tập 1: Cho tam giác ABC. Tập hợp các điểm M thoả mãn là
A. đường tròn tâm A bán kính BC.
B. đường thẳng đi qua A và song song với BC.
C. đường tròn đường kính BC.
D. đường thẳng đi qua A và vuông góc với BC.
Lời giải:
Đáp án đúng là: A
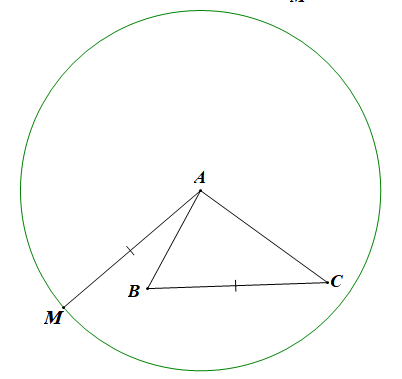
Ta có:
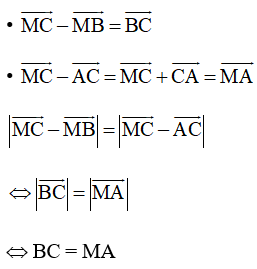
Û BC = MA
Do đó tập hợp điểm M thỏa mãn yêu cầu đề bài là đường tròn tâm A bán kính BC (như hình vẽ trên).
Vậy ta chọn phương án A.
Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
Giải SBT Toán 10 trang 66 Tập 1
Giải SBT Toán 10 trang 67 Tập 1
Giải SBT Toán 10 trang 68 Tập 1
Giải SBT Toán 10 trang 70 Tập 1
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 11: Tích vô hướng của hai vectơ
Bài 13: Các số đặc trưng đo xu thế trung tâm
Bài 14: Các số đặc trưng đo độ phân tán