Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu chi tiết sách Toán 10 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu
Giải toán lớp 10 trang 120 Tập 1 Chân trời sáng tạo
Theo bạn, địa phương nào có thời tiết ôn hòa hơn?
Lời giải:
Nếu so sánh nhiệt độ trung bình thì 2 địa phương đều có thời tiết ôn hòa dễ chịu. Tuy nhiên so sánh sự chên lệch nhiệt độ giữa các tháng thì Lâm Đồng có thời tiết ôn hòa hơn do tháng thấp nhất là khoảng 15 độ (cao hơn Lai Châu) và sự chênh lệch nhiệt độ giữa các tháng không lớn (khoảng 4 độ C).
1. Khoảng biến thiên và khoảng tứ phân vị
a) Hãy tính độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong từng nhóm.
b) Nhóm nào có thành tích chạy đồng đều hơn?
Lời giải:
a) Độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 1 là:
(phút)
Độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 2 là:
(phút)
b) Dễ thấy: nhóm 2 có thành tích chạy đồng đều hơn.
Giải toán lớp 10 trang 121 Tập 1 Chân trời sáng tạo
a) 10; 13; 15; 2; 10; 19; 2; 5; 7.
b) 15; 19; 10; 5; 9; 10; 1; 2; 5; 15.
Phương pháp giải:
Cho mẫu số liệu:
Sắp xếp mẫu số liệu theo thứ tự không giảm:
+) Khoảng biến thiên:
+) Tứ phân vị:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm:
Bước 2:
là trung vị của nửa số liệu đã sắp xếp bên trái (không bao gồm nếu n lẻ)
là trung vị của nửa số liệu đã sắp xếp bên phải (không bao gồm nếu n lẻ)
Khoảng tứ phân vị:
Lời giải:
a) Xét mẫu số liệu đã sắp xếp là:
Khoảng biến thiên của mẫu số liệu là:
Cỡ mẫu là là số lẻ nên giá trị tứ phân vị thứ hai là:
Tứ phân vị thứ nhất là trung vị của mẫu: . Do đó
Tứ phân vị thứ ba là trung vị của mẫu: . Do đó
Khoảng tứ phân vị của mẫu là:
b) Xét mẫu số liệu đã sắp xếp là:
Khoảng biến thiên của mẫu số liệu là:
Cỡ mẫu là là số chẵn nên giá trị tứ phân vị thứ hai là:
Tứ phân vị thứ nhất là trung vị của mẫu: . Do đó
Tứ phân vị thứ ba là trung vị của mẫu: . Do đó
Khoảng tứ phân vị của mẫu là:
a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm Đồng.
b) Hãy cho biết trong một năm, nhiệt độ ở địa phương nào ít thay đổi hơn.
Phương pháp giải:
a) Cho mẫu số liệu:
Sắp xếp mẫu số liệu theo thứ tự không giảm:
+) Khoảng biến thiên:
+) Tứ phân vị:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm:
Bước 2:
là trung vị của nửa số liệu đã sắp xếp bên trái (không bao gồm nếu n lẻ)
là trung vị của nửa số liệu đã sắp xếp bên phải (không bao gồm nếu n lẻ)
Khoảng tứ phân vị:
b) So sánh khoảng biến thiên
Lời giải:
a)
+) Tỉnh Lai Châu: Xét mẫu số liệu đã sắp xếp là:
Khoảng biến thiên của mẫu số liệu là:
Cỡ mẫu là là số chẵn nên giá trị tứ phân vị thứ hai là:
Tứ phân vị thứ nhất là trung vị của mẫu: . Do đó
Tứ phân vị thứ ba là trung vị của mẫu: . Do đó
Khoảng tứ phân vị của mẫu là:
+) Tỉnh Lâm Đổng: Xét mẫu số liệu đã sắp xếp là:
Khoảng biến thiên của mẫu số liệu là:
Cỡ mẫu là là số chẵn nên giá trị tứ phân vị thứ hai là:
Tứ phân vị thứ nhất là trung vị của mẫu: . Do đó
Tứ phân vị thứ ba là trung vị của mẫu: . Do đó
Khoảng tứ phân vị của mẫu là:
Giải toán lớp 10 trang 122 Tập 1 Chân trời sáng tạo
Phương pháp giải:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm:
Bước 2:
là trung vị của nửa số liệu đã sắp xếp bên trái (không bao gồm nếu n lẻ)
là trung vị của nửa số liệu đã sắp xếp bên phải (không bao gồm nếu n lẻ)
Khoảng tứ phân vị:
Bước 3: Tìm x trong mẫu sao cho hoặc
Lời giải:
Xét mẫu số liệu đã sắp xếp là:
Cỡ mẫu là là số lẻ nên giá trị tứ phân vị thứ hai là:
Tứ phân vị thứ nhất là trung vị của mẫu: . Do đó
Tứ phân vị thứ ba là trung vị của mẫu: . Do đó
Khoảng tứ phân vị của mẫu là:
Giá trị ngoại lệ x thỏa mãn hoặc .
Vậy giá trị ngoại lệ của mẫu số liệu đó là
2. Phương sai và độ lệch chuẩn
|
Cung thủ A |
8 |
9 |
10 |
7 |
6 |
10 |
6 |
7 |
9 |
8 |
|
Cung thủ B |
10 |
6 |
8 |
7 |
9 |
9 |
8 |
7 |
8 |
8 |
a) Tính kết quả trung bình của mỗi cung thủ trên
b) Cung thủ nào có kết quả các lần bắn ổn định hơn?
Lời giải:
a) Kết quả trung bình của Cung thủ A là:
Kết quả trung bình của Cung thủ A là:
b)
+) Khoảng biến thiên số điểm của cung thủ A là:
Xét mẫu số liệu đã sắp xếp là:
Cỡ mẫu là là số chẵn nên giá trị tứ phân vị thứ hai là:
Tứ phân vị thứ nhất là trung vị của mẫu:. Do đó
Tứ phân vị thứ ba là trung vị của mẫu: . Do đó
Khoảng tứ phân vị của mẫu là:
+) Khoảng biến thiên số điểm của cung thủ A là:
Xét mẫu số liệu đã sắp xếp là:
Cỡ mẫu là là số chẵn nên giá trị tứ phân vị thứ hai là:
Tứ phân vị thứ nhất là trung vị của mẫu:. Do đó
Tứ phân vị thứ ba là trung vị của mẫu: . Do đó
Khoảng tứ phân vị của mẫu là:
=> Nếu so sánh khoảng chênh lệch và khoảng tứ phân vị thì không xác định được kết quả của cung thủ nào ổn định hơn.
Giải toán lớp 10 trang 124 Tập 1 Chân trời sáng tạo
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Tuyên Quang |
25 |
89 |
72 |
117 |
106 |
177 |
156 |
203 |
227 |
146 |
117 |
145 |
|
Cà Mau |
180 |
223 |
257 |
245 |
191 |
111 |
141 |
134 |
130 |
122 |
157 |
173 |
a) Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh.
b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh.
Phương pháp giải:
Cho mẫu số liệu
Bước 1. Tính số trung bình
Bước 2: +) Tính phương sai hoặc
+) Độ lệch chuẩn
Lời giải:
+) Tuyên Quang:
Số giờ nắng trung bình
Phương sai:
Độ lệch chuẩn
+) Cà Mau:
Số giờ nắng trung bình
Phương sai:
Độ lệch chuẩn
=> Nhận xét: Ở Tuyên Quang tổng số giờ nắng theo từng tháng thay đổi nhiều hơn so với ở Cà Mau.
Bài tập
Phương pháp giải:
Từ mẫu số liệu so sánh hai giá trị: Khoảng biến thiên hoặc khoảng tứ phân vị.
+ Nếu trong mẫu không có số liệu nào quá lớn hay quá nhỏ => so sánh khoảng biến thiên
+ Nếu trong mẫu có 1 số liệu quá lớn hoặc quá nhỏ => so sánh khoảng tứ phân vị.
Lời giải:
|
Chiều cao 5 HS nam |
170 |
164 |
172 |
168 |
176 |
|
Chiều cao 5 HS nữ |
155 |
152 |
157 |
162 |
160 |
+) Khoảng biến thiên chiều cao của các học sinh nam là: 176 - 164 =12
+) Tứ phân vị:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm:
Bước 2: , là số lẻ nên
là trung vị của nửa số liệu . Do đó
là trung vị của nửa số liệu . Do đó
Khoảng tứ phân vị
+) Khoảng biến thiên chiều cao của các học sinh nữ là:
+) Tứ phân vị:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm:
Bước 2: , là số lẻ nên
là trung vị của nửa số liệu . Do đó
là trung vị của nửa số liệu . Do đó
Khoảng tứ phân vị
Kết luận: So sánh khoảng biến thiên hay tứ phân vị thì theo mẫu số liệu trên, chiều cao của 5 bạn nữ là đồng đều hơn.
a) 6; 8; 3; 4; 5; 6; 7; 2; 4.
b) 13; 37; 64; 12; 26; 43; 29; 23.
Phương pháp giải:
Cho mẫu số liệu
+) số trung bình
+) phương sai hoặc
=> Độ lệch chuẩn
Sắp xếp mẫu số liệu theo thứ tự không giảm:
+) Khoảng biến thiên:
Tứ phân vị:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm:
Bước 2:
là trung vị của nửa số liệu đã sắp xếp bên trái (không bao gồm nếu n lẻ)
là trung vị của nửa số liệu đã sắp xếp bên phải (không bao gồm nếu n lẻ)
+) Khoảng tứ phân vị:
+) x là giá trị ngoại lệ trong mẫu nếu hoặc
Lời giải:
a) Số trung bình: .
Phương sai mẫu số liệu là:
(62 + 82 + 32 + 42 + 52 + 62 + 72 + 22 + 42) – 52 = .
Độ lệch chuẩn mẫu số liệu là: .
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
2; 3; 4; 4; 5; 6; 6; 7; 8.
Khoảng biến thiên của mẫu là: R = 8 – 2 = 6.
Vì cỡ mẫu là 9 là số lẻ nên tứ phân vị thứ hai là Q2 = 5.
Tứ phân vị thứ nhất là trung vị của mẫu: 2; 3; 4; 4. Do đó Q1 = 3,5.
Tứ phân vị thứ ba là trung vị của mẫu: 6; 6; 7; 8. Do đó Q3 = 6,5.
Khoảng tứ phân vị của mẫu là: ∆Q = 6,5 – 3,5 = 3.
Ta có: Q3 + 1,5∆Q = 6,5 + 1,5 . 3 = 11 và Q1 – 1,5∆Q = 3,5 – 1,5 . 3 = – 1.
Do đó mẫu số liệu không có giá trị ngoại lệ.
b)
Số trung bình: .
Phương sai mẫu số liệu là:
(132 + 372 + 642 + 122 + 262 + 432 + 292 + 232) – (30,875)2 ≈ 255,86.
Độ lệch chuẩn mẫu số liệu là: .
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
12; 13; 23; 26; 29; 37; 43; 64.
Khoảng biến thiên của mẫu là: R = 64 – 12 = 52.
Vì cỡ mẫu là 8 là số chẵn nên tứ phân vị thứ hai là Q2 = .
Tứ phân vị thứ nhất là trung vị của mẫu: 12; 13; 23; 26. Do đó Q1 = 18.
Tứ phân vị thứ ba là trung vị của mẫu: 29; 37; 43; 64. Do đó Q3 = 40.
Khoảng tứ phân vị của mẫu là: ∆Q = 40 – 18 = 22.
Ta có: Q3 + 1,5∆Q = 40 + 1,5 . 22 = 73 và Q1 – 1,5∆Q = 18 – 1,5 . 22 = – 15.
Do đó mẫu số liệu không có giá trị ngoại lệ.
Giải toán lớp 10 trang 125 Tập 1 Chân trời sáng tạo
a)
b)
|
Giá trị |
0 |
1 |
2 |
3 |
4 |
|
Tần suất |
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
Phương pháp giải:
Cho bảng số liệu:
|
Giá trị |
|
|
… |
|
|
Tần số |
|
|
… |
|
+) Số trung bình:
+) Phương sai
=> Độ lệch chuẩn
Sắp xếp mẫu số liệu theo thứ tự không giảm:
+) Khoảng biến thiên:
Tứ phân vị:
+) Khoảng tứ phân vị:
Lời giải:
a) +) Số trung bình
+) phương sai hoặc
=> Độ lệch chuẩn
+) Khoảng biến thiên:
Tứ phân vị:
+) Khoảng tứ phân vị:
b) Giả sử cỡ mẫu . Khi đó mẫu số liệu trở thành:
|
Giá trị |
0 |
1 |
2 |
3 |
4 |
|
Tần số |
1 |
2 |
4 |
2 |
1 |
+) Số trung bình
+) phương sai hoặc
=> Độ lệch chuẩn
+) Khoảng biến thiên:
Tứ phân vị:
+) Khoảng tứ phân vị:
Mẫu 1: 0,1; 0,3; 0,5; 0,5; 0,3; 0,7.
Mẫu 2: 1,1; 1,3; 1,5; 1,5; 1,3; 1,7.
Mẫu 3: 1; 3; 5; 5; 3; 7.
Phương pháp giải:
+) số trung bình
+) Phương sai hoặc
+) Độ lệch chuẩn
Lời giải:
Mẫu 1:
+) Số trung bình:
+) Phương sai
+) Độ lệch chuẩn
Mẫu 2:
+) Số trung bình:
+) Phương sai
+) Độ lệch chuẩn
Mẫu 3:
+) Số trung bình:
+) Phương sai
+) Độ lệch chuẩn
Kết luận:
Số liệu ở mẫu 2 hơn số liệu ở mẫu 1 là 1 đơn vị, số trung bình của mẫu 2 hơn số trung bình mẫu 1 là 1 đơn vị, còn phương sai và độ lệch chuẩn là như nhau.
Số liệu ở mẫu 3 gấp 10 lần số liệu mẫu 1, số trung bình, phương sai và độ lệch chuẩn của mẫu 3 lần lượt gấp 10 lần, 100 lần và 10 lần mẫu 1.
a) Hãy tính độ lệch chuẩn và khoảng biến thiên của sản lượng lúa từng tỉnh.
b) Tỉnh nào có sản lượng lúa ổn định hơn? Tại sao?
Phương pháp giải:
a)
+) Tình độ lệch chuẩn:
Bước 1: Tìm số trung bình
Bước 2: Tính phương sai hoặc
=> Độ lệch chuẩn
+) Khoảng biến thiên = số liệu lớn nhất – số liệu nhỏ nhất
b)
So sánh khoảng biến thiên và độ lệch chuẩn, tỉnh nào có khoảng biến thiên và độ lệch chuẩn nhỏ hơn thì có sản lượng lúa ổn định hơn.
Lời giải:
a)
Tỉnh Thái Bình:
Số trung bình
Phương sai
=> Độ lệch chuẩn
+) Khoảng biến thiên
Tỉnh Hậu Giang:
Số trung bình
Phương sai
=> Độ lệch chuẩn
+) Khoảng biến thiên
b)
So sánh khoảng biến thiên và độ lệch chuẩn ta đều thấy tỉnh Hậu Giang có sản lượng lúa ổn định hơn.
a) Hãy tìm số trung bình, mốt, tứ phân vị và độ lệch chuẩn của hai mẫu số liệu lấy từ nhà máy A và nhà máy B.
b) Hãy tìm các giá trị ngoại lệ trong mỗi mẫu số liệu trên. Công nhân nhà máy nào có mức lương cao hơn? Tại sao?
Phương pháp giải:
a)
+) Số trung bình:
+) Mốt: là giá trị xuất hiện nhiều nhất trong mẫu số liệu.
+) Tứ phân vị:
Sắp xếp mẫu số liệu theo thứ tự không giảm:
là trung vị của nửa số liệu đã sắp xếp bên trái (không bao gồm nếu n lẻ)
là trung vị của nửa số liệu đã sắp xếp bên phải (không bao gồm nếu n lẻ)
+) Độ lệch chuẩn
Tính phương sai
b)
+) x là giá trị ngoại lệ nếu hoặc
+) So sánh trung vị (do một mẫu có số liệu quá lớn so với các số liệu khác): nhà máy nào có trung vị lớn hơn thì có mức lương cao hơn.
Lời giải:
a)
* Nhà máy A:
+ Số trung bình mức lương hàng tháng: .
+ Giá trị 4 và 5 có tần số lớn nhất nên mốt của mẫu số liệu ở nhà máy A là 4 và 5.
+ Sắp xếp các số liệu theo thứ tự không giảm, ta được:
4; 4; 4; 5; 5; 5; 6; 47.
Vì cỡ mẫu là 8 là số chẵn nên tứ phân vị thứ hai là Q2A = 5.
Tứ phân vị thứ nhất là trung vị của mẫu: 4; 4; 4; 5. Do đó Q1A = 4.
Tứ phân vị thứ ba là trung vị của mẫu: 5; 5; 6; 47. Do đó Q3A = 5,5.
+ Phương sai mẫu:
(42 + 52 + 52 + 472 + 52 + 62 + 42 + 42) – 102 = 196.
+ Độ lệch chuẩn: SA = .
* Nhà máy B:
+ Số trung bình mức lương hàng tháng: .
+ Giá trị 9 có tần số lớn nhất nên mốt của mẫu số liệu ở nhà máy B là 9.
+ Sắp xếp các số liệu theo thứ tự không giảm, ta được:
2; 8; 9; 9; 9; 9; 9; 10; 11.
Vì cỡ mẫu là 9 là số lẻ nên tứ phân vị thứ hai là Q2B = 9.
Tứ phân vị thứ nhất là trung vị của mẫu: 2; 8; 9; 9. Do đó Q1B = 8,5.
Tứ phân vị thứ ba là trung vị của mẫu: 9; 9; 10; 11. Do đó Q3B = 9,5.
+ Phương sai mẫu:
(22 + 82 + 92 + 92 + 92 + 92 + 92 + 102 + 112) – 8,42 = 6,55.
+ Độ lệch chuẩn: SB = .
b)
+ Khoảng tứ phân vị của mẫu số liệu ở nhà máy A là: ∆QA = 5,5 – 4 = 1,5.
Ta có: Q3A + 1,5∆QA = 5,5 + 1,5 . 1,5 = 7,75 và Q1A – 1,5∆QA = 4 – 1,5 . 1,5 = 1,75.
Do đó giá trị ngoại lệ trong mẫu số liệu ở nhà máy A là 47.
Lý thuyết Các số đặc trưng đo mức độ phân tán của mẫu số liệu
1. Khoảng biến thiên và khoảng tứ phân vị
1.1. Khoảng biến thiên và khoảng tứ phân vị
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
x1 ≤ x2 ≤ … ≤ xn.
• Khoảng biến thiên của một mẫu số liệu, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó, tức là:
R = xn – x1.
• Khoảng tứ phân vị, kí hiệu là ∆Q, là hiệu giữa Q3 và Q1, tức là:
∆Q = Q3 – Q1.
Ví dụ: Hãy tính khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu:
10; 3; 5; 7; 20; 1; 4; 9.
Hướng dẫn giải
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được: 1; 3; 4; 5; 7; 9; 10; 20.
- Khoảng biến thiên của mẫu số liệu là R = 20 – 1 = 19.
- Cỡ mẫu là n = 8, là số chẵn nên giá trị tứ phân vị thứ hai là Q2 = 6.
- Tứ phân vị thứ nhất là trung vị của mẫu: 10; 3; 5; 7. Do đó Q1 = 4.
- Tứ phân vị thứ 3 là trung vị của mẫu: 7; 9; 10; 20. Do đó Q3 = 9,5.
- Khoảng tứ phân vị của mẫu là: ∆Q = 9,5 – 4 = 5,5.
1.2. Ý nghĩa của khoảng biến thiên và khoảng tứ phân vị
Khoảng biến thiên đặc trưng cho độ phân tán của toàn bộ mẫu số liệu.
Khoảng tứ phân vị đặc trưng cho độ phân tán của một nửa các số liệu, có giá trị thuộc đoạn từ Q1 đến Q3 trong mẫu.
Khoảng tứ phân vị không bị ảnh hưởng bởi các giá trị rất lớn hoặc rất bé trong mẫu.
Ví dụ: Dưới đây là bảng số liệu thống kê của Biểu đồ nhiệt độ trung bình các tháng trong năm 2019 của hai tỉnh Lai Châu và Lâm Đồng (được đề cập đến ở hoạt động khởi động của bài học).

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm Đồng.
b) Hãy cho biết trong một năm, nhiệt độ ở địa phương nào ít thay đổi hơn.
Hướng dẫn giải
a)
* Tỉnh Lai Châu:
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
14,2; 14,8; 18,6; 18,8; 20,3; 21,0; 22,7; 23,5; 23,6; 24,2; 24,6; 24,7.
+ Khoảng biến thiên của mẫu số liệu là: R = 24,7 – 14,2 = 10,5.
+ Cỡ mẫu là n = 12 là số chẵn nên giá trị tứ phân vị thứ hai là:
Q2 = .
+ Tứ phân vị thứ nhất là trung vị của mẫu: 14,2; 14,8; 18,6; 18,8; 20,3; 21,0.
Do đó Q1 = .
+ Tứ phân vị thứ ba là trung vị của mẫu: 22,7; 23,5; 23,6; 24,2; 24,6; 24,7.
Do đó Q3 = .
+ Khoảng tứ phân vị của mẫu là: ∆Q = 23,9 – 18,7 = 5,2.
* Tỉnh Lâm Đồng:
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
16,0; 16,3; 17,4; 17,5; 18,5; 18,6; 18,7; 19,3; 19,5; 19,8; 20,2; 20,3.
+ Khoảng biến thiên của mẫu số liệu là: R' = 20,3 – 16,0 = 4,3.
+ Cỡ mẫu là n = 12 là số chẵn nên giá trị tứ phân vị thứ hai là:
Q'2 = .
+ Tứ phân vị thứ nhất là trung vị của mẫu: 16,0; 16,3; 17,4; 17,5; 18,5; 18,6.
Do đó Q'1 = .
+ Tứ phân vị thứ ba là trung vị của mẫu: 18,7; 19,3; 19,5; 19,8; 20,2; 20,3.
Do đó Q'3 = .
+ Khoảng tứ phân vị của mẫu là: ∆'Q = 19,65 – 17,45 = 2,2.
b) Xét về cả khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của cả hai tỉnh, ta thấy: 10,5 > 4,3 hay R > R' và 5,2 > 2,2 hay ∆Q > ∆'Q.
Điều đó có nghĩa là trong một năm, nhiệt độ ở Lâm Đồng ít thay đổi hơn.
1.3. Giá trị ngoại lệ
Khoảng tứ phân vị được dùng để xác định các giá trị ngoại lệ trong mẫu, đó là các giá trị quá nhỏ hay quá lớn so với đa số các giá trị của mẫu. Cụ thể, phần tử x trong mẫu là giá trị ngoại lệ nếu x > Q3 + 1,5∆Q hoặc x < Q1 – 1,5∆Q.
Sự xuất hiện của các giá trị ngoại lệ làm cho số trung bình và phạm vi của mẫu thay đổi lớn. Do đó, khi mẫu có giá trị ngoại lệ, người ta thường sử dụng trung vị và khoảng tứ phân vị để đo mức độ tập trung và mức độ phân tán của đa số các phần tử trong mẫu số liệu.
Ví dụ: Trong ví dụ ở phần 1.1, ta có:
Q1 – 1,5∆Q = 4 – 1,5 . 5,5 = – 4,25
Q3 + 1,5∆Q = 9,5 + 1,5 . 5,5 = 17,75
Do đó, mẫu có một giá trị ngoại lệ là 20.
2. Phương sai và độ lệch chuẩn
2.1. Công thức tính phương sai và độ lệch chuẩn
* Giả sử ta có một mẫu số liệu là x1, x2, …, xn.
• Phương sai của mẫu số liệu này, kí hiệu là S2, được tính bởi công thức:
trong đó là số trung bình của mẫu số liệu.
• Căn bậc hai của phương sai được gọi là độ lệch chuẩn, kí hiệu là S.
Chú ý: Có thể biến đổi công thức tính phương sai ở trên thành:
.
Trong thống kê, người ta cũng quan tâm đến phương sai hiệu chỉnh, kí hiệu là , được tính bởi công thức:
.
* Giả sử mẫu số liệu được cho dưới dạng bảng tần số:
|
Giá trị |
x1 |
x2 |
… |
xk |
|
Tần số |
n1 |
n2 |
… |
nk |
Khi đó, công thức tính phương sai trở thành:
trong đó n = n1 + n2 + … + nk.
Có thể biến đổi công thức tính phương sai trên thành
.
Ví dụ: Tính phương sai và độ lệch chuẩn của mẫu số liệu sau:
8; 10; 9; 7; 6; 10; 6; 7; 8; 9.
Hướng dẫn giải
Cỡ mẫu n = 10.
Số trung bình: (8 + 10 + 9 + 7 + 6 + 10 + 6 + 7 + 8 + 9) : 10 = 8.
Phương sai mẫu số liệu là:
S2 = (82 + 102 + 92 + 72 + 62 + 102 + 62 + 72 + 82 + 92) – 82 = 2.
Độ lệch chuẩn mẫu số liệu là S = .
Ví dụ: Điều tra số con của mỗi hộ gia đình trong tổ dân cư xóm 2, kết quả được ghi lại ở bảng sau:
|
Số con |
0 |
1 |
2 |
3 |
4 |
|
Số hộ gia đình |
4 |
4 |
8 |
3 |
1 |
Tính phương sai và độ lệch chuẩn của mẫu số liệu.
Hướng dẫn giải
Tổng số hộ gia đình là: n = 4 + 4 + 8 + 3 + 1 = 20 (hộ gia đình).
Số trung bình của mẫu số liệu trên là
(4 . 0 + 4 . 1 + 8 . 2 + 3 . 3 + 1 . 4) = 1,65
Phương sai của mẫu số liệu trên là:
S2 = (4 . 02 + 4 . 12 + 8 . 22 + 3 . 32 + 1 . 42) – 1,652 = 1,2275
Độ lệch chuẩn của mẫu số liệu trên là:
.
2.2. Ý nghĩa của phương sai và độ lệch chuẩn
Phương sai là trung bình cộng của các bình phương độ lệch từ mỗi giá trị của mẫu số liệu đến số trung bình.
Phương sai và độ lệch chuẩn được dùng để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình. Phương sai và độ lệch chuẩn càng lớn thì các giá trị của mẫu càng cách xa nhau (có độ phân tán lớn).
Ví dụ: Bảng dưới đây thống kê tổng số giờ nắng trong năm 2019 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở Tuyên Quang và Cà Mau.
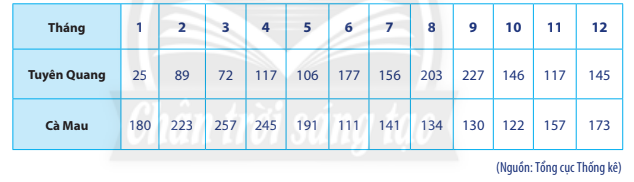
a) Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh.
b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh.
Hướng dẫn giải
a)
* Tỉnh Tuyên Quang:
+ Số trung bình:
.
+ Phương sai mẫu số liệu ở tỉnh Tuyên Quang là:≈ 2920,34.
+ Độ lệch chuẩn mẫu số liệu ở tỉnh Tuyên Quang là:
S1 = .
* Tỉnh Cà Mau:
+ Số trung bình:
.
+ Phương sai mẫu số liệu ở tỉnh Cà Mau là:
(1802 + 2232 + 2572 + 2452 + 1912 + 1112 + 1412 + 1342 + 1302 + 1222 + 1572 + 1732) – 1722 = 2183.
+ Độ lệch chuẩn mẫu số liệu ở tỉnh Cà Mau là:
S2 = .
b) Phương sai mẫu và độ lệch chuẩn mẫu số liệu ở tỉnh Tuyên Quang cao hơn tỉnh Cà Mau nên tổng số giờ nắng trong năm 2019 theo từng tháng ở tỉnh Tuyên Quang có độ phân tán cao hơn ở tỉnh Cà Mau. Do đó, sự thay đổi tổng số giờ nắng theo từng tháng ở tỉnh Cà Mau ổn định (có ít sự thay đổi) hơn so với tỉnh Tuyên Quang.
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu
Bài 2: Dùng bảng tính để tính các số đặc trưng của mẫu số liệu thống kê