Cho tam giác đều ABC có độ dài cạnh là 6 cm. trên tia BA, CA lần lượt lấy điểm D,E

Cho tam giác đều ABC có độ dài cạnh là 6 cm. trên tia BA, CA lần lượt lấy điểm D,E

Van Anh Ngày: 05-09-2023 Lớp 8

1.5 K

Với giải Bài 15 trang 92 SBT Toán lớp 8 Cánh diều chi tiết trong Bài 3: Hình thang cân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 3: Hình thang cân

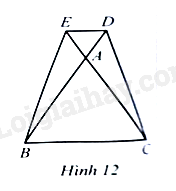
Bài 15 trang 92 SBT Toán 8 Tập 1: Cho tam giác đều $A B C$ có độ dài cạnh là 6 cm. trên tia $B A, C A$ lần lượt lấy điểm $D, E$ sao cho $A D = A E = 2 c m$ (Hình 12)

a) Tứ giác $B C D E$ là hình gì? Vì sao?

b) Tính độ dài đoạn thẳng $C D$ (làm tròn kết quả đến hàng phần mười của centimet).

Sách bài tập Toán 8 Bài 3 (Cánh diều): Hình thang cân (ảnh 5)

Lời giải:

Sách bài tập Toán 8 Bài 3 (Cánh diều): Hình thang cân (ảnh 6)

a) Tam giác đều $A B C$ có $A B = B C = A C = 6 c m$ ; $\hat{B A C} = \hat{C B A} = \hat{A C B} = 60^{\circ}$

Ta có: $\hat{D A E} = \hat{B A C}$ (hai góc đối đỉnh) nên $\hat{D A E} = 60^{\circ}$

Tam giác $A D E$ có $A D = A E$ và $\hat{D A E} = 60^{\circ}$ nên $A D E$ là tam giác đều. Suy ra $\hat{A D E} = 60^{\circ}$ . Do đó $\hat{C B A} = \hat{A D E}$ (vì cùng bằng $60^{\circ}$ ). Mà $\hat{C B A}$ và $\hat{A D E}$ nằm ở vị trí so le trong, suy ra $B C / / D E$ .

Ta có: $A B = A C$ và $A D = A E$ nên $B D = C E$ .

Tứ giác $B C D E$ có $B C / / D E$ và $B D = C E$ nên $B C D E$ là hình thang cân.

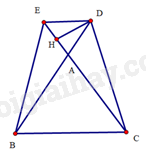
b) Kẻ $D H$ vuông góc với $C E$ tại $H$ .

$Δ A D H = Δ E D H$ (cạnh huyền – cạnh góc vuông)

Suy ra $A H = E H = \frac{A E}{2} = 1 c m$

Trong tam giác $A D H$ vuông tại $H$ , ta có: $C D^{2} = C H^{2} + D H^{2}$ . Suy ra $C D^{2} = 52$

Vậy $C D = \sqrt{52} \approx 7, 2 (c m)$ .

Xem thêm lời giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 11 trang 92 SBT Toán 8 Tập 1: Cho tứ giác $A B C D$ có $\hat{C} = \hat{D}$ và $A D = B C$ . Chứng minh tứ giác $A B C D$ là hình thang cân....

Bài 12 trang 92 SBT Toán 8 Tập 1: Cho hình thang cân $A B C D$ có $A B / / C D, A B < C D$ , hai đường chéo $A C$ và $B D$ cắt nhau tại $P$ , hai cạnh bên $A D$ và $B C$ kéo dài cắt nhau tại $Q$ . Chứng minh $P Q$ là đường trung trực của hai đáy hình thang cân $A B C D$ ....

Bài 13 trang 92 SBT Toán 8 Tập 1: Cho hình thang cân $A B C D$ có $A B / / C D, A B = 3 m c, C D = 6 c m, A D = 2.5 c m$ . Gọi $M, N$ lần lượt là hình chiếu của $A, B$ trên đường thẳng $C D$ . Tính độ dài các đoạn thẳng $D M, D N, A M$ ....

Bài 14 trang 92 SBT Toán 8 Tập 1: Cho tam giác $A B C$ cân tại $A$ . Lấy điểm $M, N$ lần lượt trên cạnh $A B, A C$ sao cho $A M = A N$ ....

Bài 15 trang 92 SBT Toán 8 Tập 1: Cho tam giác đều $A B C$ có độ dài cạnh là 6 cm. trên tia $B A, C A$ lần lượt lấy điểm $D, E$ sao cho $A D = A E = 2 c m$ (Hình 12)....

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

162

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

135

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

112

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

108

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.