Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian

Admin Vietjack Ngày: 25-09-2024 Lớp 11

2.7 K

Với giải sách bài tập Toán 11 Bài 1: Đường thẳng và mặt phằng trong không gian sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 1: Đường thẳng và mặt phằng trong không gian

Giải SBT Toán 11 trang 94

Bài 1 trang 94 SBT Toán 11: Cho hình chóp tứ giác S.ABCD có ABCD là hình bình hành. Điểm M thuộc cạnh SC. Trong các mặt phẳng sau, điểm M nằm trên mặt phẳng nào?

A. (ABCD)

B. (SAC)

C. (SAB)

D. (SAD)

Lời giải:

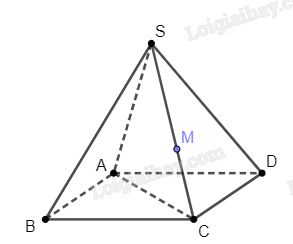
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

Theo hình vẽ, ta thấy SC nằm trong mặt (SAC).

Do $M \in S C$ nên M nằm trên mặt phẳng (SAC).

Đáp án đúng là B.

Bài 2 trang 94 SBT Toán 11: Cho hình tứ diện ABCD. Giao tuyến của hai mặt phẳng (ABC) và (CDA) là đường thẳng:

A. AB

B. BD

C. CD

D. AC

Lời giải:

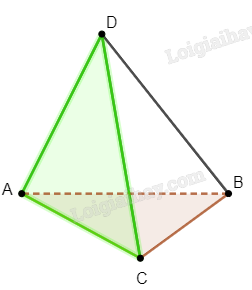
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

Xét hai mặt phẳng (ABC) và (CDA), ta nhận thấy hai mặt phẳng này có hai điểm chung là A và C, do đó giao tuyến của hai mặt phẳng này là AC.

Đáp án đúng là D.

Bài 3 trang 94 SBT Toán 11: Một đồ vật trang trí có bốn mặt phân biệt là các tam giác (xem hình dưới đây). Vẽ hình hiểu diễn của đồ vật đó.

Lời giải:

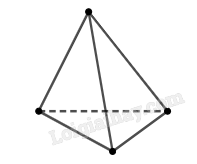
Do đồ vật trang trí có 4 mặt là các tam giác, nên nó có hình dạng một tứ diện.

Hình biểu diễn của nó như sau:

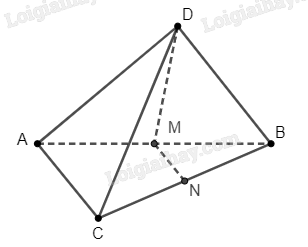
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

Bài 4 trang 94 SBT Toán 11: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, C, D không cùng nằm trong một mặt phẳng.

Lời giải:

Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

Do $N$ là trung điểm của $B C$ , nên 4 điểm $B$ , $N$ , $C$ , $D$ cùng nằm trong mặt phẳng.

Giả sử 4 điểm $M$ , $N$ , $C$ , $D$ cùng nằm trong một mặt phẳng.

Điều này có nghĩa là $M \in (N C D)$ .

Do bốn điểm $B$ , $N$ , $C$ , $D$ cùng nằm trong mặt phẳng, ta suy ra $M \in (B C D)$ .

Điểm $M$ và điểm $B$ cùng nằm trong mặt phẳng $(B C D)$ , nên $B M \subset (B C D)$ .

Mặt khác, do $M$ là trung điểm của $A B$ , nên $A \in B M$ .

Suy ra $A \in (B C D)$ . Điều này là vô lí do $A B C D$ là tứ diện nên bốn điểm $A$ , $B$ , $C$ , $D$ không cùng nằm trong một mặt phẳng.

Giải SBT Toán 11 trang 95

Bài 5 trang 95 SBT Toán 11: Cho hai mặt phẳng (P), (Q) cắt nhau theo giao tuyến d và hai đường thẳng a, b lần lượt nằm trong (P), (Q). Chứng minh rằng nếu hai đường thẳng a, b cắt nhau thì giao điểm của chúng thuộc đường thẳng d.

Lời giải:

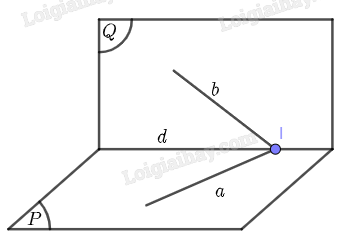
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

Gọi $I$ là giao điểm của hai đường thẳng $a$ và $b$ . Suy ra ${\begin{cases} I \in a \\ I \in b \end{cases}$

Vì $a \subset (P)$ và $b \subset (Q)$ , ta suy ra ${\begin{cases} I \in (P) \\ I \in (Q) \end{cases}$ , tức là $I$ thuộc giao tuyến của hai mặt phẳng $(P)$ và $(Q)$ . Mà $(P) \cap (Q) = d$ , suy ra $I \in d$ .

Bài toán được chứng minh.

Bài 6 trang 95 SBT Toán 11: Cho tứ diện $A B C D$ . Trên các cạnh $A C, C D$ lần lượt lấy các điểm $E, F$ sao cho $C E = 3 E A, D F = 2 F C$ .

a) Xác định giao tuyến của mặt phẳng $(B E F)$ với các mặt phẳng $(A B C)$ , $(A C D)$ , $(B C D)$ .

b) Xác định giao điểm $K$ của đường thẳng $A D$ với mặt phẳng $(B E F)$ .

c) Xác định giao tuyến của hai mặt phẳng $(B E F)$ và $(A B D)$ .

Lời giải:

Giao tuyến của $(B E F)$ và $(A B C)$ :

Ta có $B \in (B E F) \cap (A B C)$ .

Mặt khác, ta có ${\begin{cases} E \in (B E F) \\ E \in A C \subset (A B C) \end{cases} \Rightarrow E \in (B E F) \cap (A B C)$ .

Như vậy giao tuyển của $(B E F)$ và $(A B C)$ là đường thẳng $B E$ .

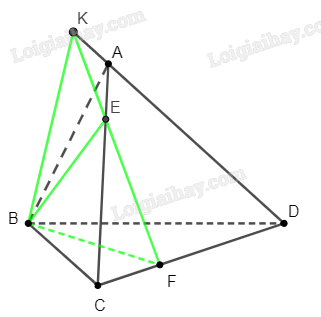
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

Giao tuyến của $(B E F)$ và $(A C D)$ :

Ta có ${\begin{cases} F \in (B E F) \\ F \in C D \subset (A C D) \end{cases} \Rightarrow F \in (B E F) \cap (A C D)$ .

Mặt khác, ${\begin{cases} E \in (B E F) \\ E \in A C \subset (A C D) \end{cases} \Rightarrow E \in (B E F) \cap (A C D)$ .

Như vậy giao tuyển của $(B E F)$ và $(A C D)$ là đường thẳng $E F$ .

Giao tuyến của $(B E F)$ và $(B C D)$ :

Ta có $B \in (B E F) \cap (B C D)$

Mặt khác, ${\begin{cases} F \in (B E F) \\ F \in C D \subset (B C D) \end{cases} \Rightarrow F \in (B E F) \cap (B C D)$

Như vậy giao tuyển của $(B E F)$ và $(B C D)$ là đường thẳng $B F$ .

b) Trên mặt phẳng $(A C D)$ , lấy $K$ là giao điểm của $A D$ và $E F$ .

Ta có ${K} = A D \cap E F$ , mà $E F \subset (B E F)$ .

Suy ra ${K} = A D \cap (B E F)$ , tức $K$ là giao điểm của $A D$ và $(B E F)$ .

c) Ta có $B \in (B E F) \cap (A B D)$ .

Theo câu b, ta có $K \in A D \cap (B E F) \Rightarrow {\begin{cases} K \in A D \\ K \in (B E F) \end{cases}$

Mà $A D \in (A B D)$ nên ta suy ra ${\begin{cases} K \in (A B D) \\ K \in (B E F) \end{cases} \Rightarrow K \in (A B D) \cap (B E F)$ .

Vậy giao tuyến của hai mặt phẳng $(B E F)$ và $(A B D)$ là đường thẳng $B K$ .

Bài 7 trang 95 SBT Toán 11: Cho hình chóp $S . A B C D$ có đáy là hình bình hành. Gọi $M, N, P$ lần lượt là trung điểm của các cạnh $S A, B C, C D$ .

a) Xác định giao điểm của đường thẳng $N P$ với mặt phẳng $(S A B)$ .

b) Xác định giao tuyến của mặt phẳng $(M N P)$ với các mặt phẳng $(S A B), (S A D), (S B C), (S C D)$ .

Lời giải:

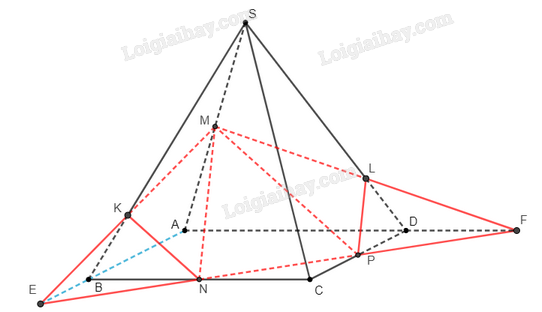
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

a) Xét mặt phẳng $(A B C D)$ , gọi $E$ là giao điểm của $A B$ và $N P$ .

Ta có ${E} = A B \cap N P$ , mà $N P \subset (M N P)$ nên ${E} = (S A B) \cap N P$ .

Giao tuyến của $(M N P)$ và $(S A B)$ :

Ta có ${\begin{cases} M \in S A \subset (S A B) \\ M \in (M N P) \end{cases} \Rightarrow M \in (S A B) \cap (M N P)$ .

Mặt khác, theo câu a, ta có ${\begin{cases} E \in A B \subset (S A B) \\ E \in N P \subset (M N P) \end{cases} \Rightarrow E \in (S A B) \cap (M N P)$ .

Từ đó, giao tuyến của hai mặt phẳng $(S A B)$ và $(M N P)$ là đường thẳng $M E$ .

Giao tuyến của $(M N P)$ và $(S A D)$ :

Trên mặt phẳng $(A B C D)$ , gọi $F$ là giao điểm của $A D$ và $N P$ .

Vì $F$ là giao điểm của $A D$ và $N P$ , ta suy ra ${\begin{cases} F \in A D \\ F \in N P \end{cases}$ .

Do $A D \subset (S A D)$ , $N P \subset (M N P)$ nên ta có ${\begin{cases} F \in (S A D) \\ F \in (M N P) \end{cases} \Rightarrow F \in (S A D) \cap (M N P)$ .

Hơn nữa, ta cũng có ${\begin{cases} M \in S A \subset (S A D) \\ M \in (M N P) \end{cases} \Rightarrow M \in (S A D) \cap (M N P)$ .

Vậy giao tuyến của hai mặt phẳng $(S A D)$ và $(M N P)$ là đường thẳng $M F$ .

Giao tuyến của $(M N P)$ và $(S B C)$ :

Ta có $M E$ là giao tuyến của hai mặt phẳng $(S A B)$ và $(M N P)$ $\Rightarrow M E \subset (S A B)$ .

Trên mặt phẳng $(S A B)$ , gọi ${K} = M E \cap S B$ .

Suy ra ${\begin{cases} K \in M E \subset (M N P) \\ K \in S B \subset (S B C) \end{cases} \Rightarrow K \in (M N P) \cap (S B C)$ .

Hơn nữa, ta có ${\begin{cases} N \in (M N P) \\ N \in B C \subset (S B C) \end{cases} \Rightarrow N \in (M N P) \cap (S B C)$ .

Vậy giao tuyến của hai mặt phẳng $(S B C)$ và $(M N P)$ là đường thẳng $N K$ .

Giao tuyến của $(M N P)$ và $(S C D)$ :

Ta có $M F$ là giao tuyến của hai mặt phẳng $(S A D)$ và $(M N P)$ $\Rightarrow M F \subset (S A D)$ .

Trên mặt phẳng $(S A D)$ , gọi ${L} = M F \cap S D$ .

Suy ra ${\begin{cases} L \in M F \subset (M N P) \\ L \in S D \subset (S C D) \end{cases} \Rightarrow L \in (M N P) \cap (S C D)$ .

Hơn nữa, ta có ${\begin{cases} P \in (M N P) \\ P \in C D \subset (S C D) \end{cases} \Rightarrow P \in (M N P) \cap (S C D)$ .

Vậy giao tuyến của hai mặt phẳng $(S C D)$ và $(M N P)$ là đường thẳng $L P$ .

Bài 8 trang 95 SBT Toán 11: Cho hình chóp $S . A B C D$ có đáy là hình bình hành. Gọi $M, N, P$ lần lượt là trung điểm của các cạnh $S A, S B, S C$ .

a) Xác định giao điểm $I$ của đường thẳng $M P$ với mặt phẳng $(S B D)$ .

b) Xác định giao điểm $Q$ của đường thẳng $S D$ với mặt phẳng $(M N P)$ .

Lời giải:

a) Trên mặt phẳng $(A B C D)$ , gọi ${O} = A C \cap B D$ .

Trên mặt phẳng $(S A C)$ , gọi ${I} = M P \cap S O$ .

Do $S O \subset (S B D)$ , ta suy ra ${I} = M P \cap (S B D)$ .

Vậy $I$ là giao điểm của $M P$ và $(S B D)$ .

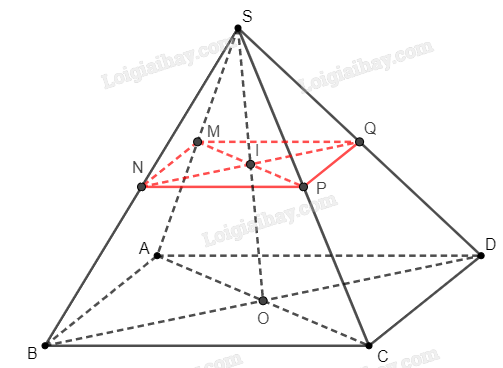
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

b) Trên mặt phẳng $(S B D)$ , gọi ${Q} = N I \cap S D$ .

Do $N I \subset (M N P)$ , ta suy ra ${Q} = (M N P) \cap S D$ .

Vậy $Q$ là giao điểm của $S D$ và $(M N P)$ .

Bài 9 trang 95 SBT Toán 11: Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi O là giao điểm của AC và BD. Trên SO lấy điểm I sao cho SI = 2IO.

a) Xác định các giao điểm M, N lần lượt của SA, SD với mặt phẳng (IBC).

b*) Chứng minh rằng các đường thẳng AD, BC và MN đồng quy.

Lời giải:

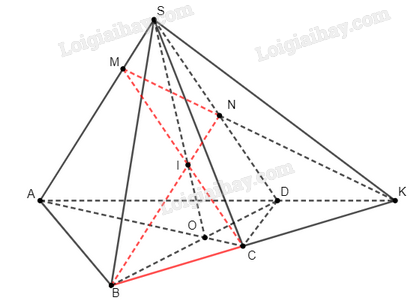
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian (ảnh 1)

Giao điểm $M$ của $S A$ và $(I B C)$ :

Ta nhận xét rằng $I \in S O \subset (S A C) \Rightarrow C I \subset (S A C)$ .

Trên mặt phẳng $(S A C)$ , gọi ${M} = C I \cap S A$ .

Do $I C \subset (I B C)$ , nên ${M} = (I B C) \cap S A$ .

Vậy $M$ là giao điểm của $(I B C)$ và $S A$ .

Giao điểm $N$ của $S D$ và $(I B C)$ :

Ta nhận xét rằng $I \in S O \subset (S B D) \Rightarrow B I \subset (S B D)$ .

Trên mặt phẳng $(S B D)$ , gọi ${N} = B I \cap S D$ .

Do $I B \subset (I B C)$ , nên ${N} = (I B C) \cap S D$ .

Vậy $N$ là giao điểm của $(I B C)$ và $S D$ .

b) Trên mặt phẳng $(A B C D)$ , gọi $K$ là giao điểm của $A D$ và $B C$ .

Ta có ${\begin{cases} M \in S A \subset (S A D) \\ M \in (I B C) \end{cases} \Rightarrow M \in (S A D) \cap (I B C)$ .

Mặt khác, ${\begin{cases} N \in S D \subset (S A D) \\ N \in (I B C) \end{cases} \Rightarrow N \in (S A D) \cap (I B C)$ .

Vậy giao tuyến của $(S A D)$ và $(I B C)$ là đường thẳng $M N$ .

Do $A D \in (S A D)$ , $B C \in (I B C)$ , ${K} = A D \cap B C$ , ta suy ra $K$ nằm trên giao tuyến của $(S A D)$ và $(I B C)$ , tức là $K \in M N$ .

Vậy ba đường thẳng $A D$ , $B C$ , $M N$ cắt nhau tại $K$ .

Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song trong không gian

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song

Bài 5: Hình lăng trụ và hình hộp

Lý thuyết Đường thẳng và mặt phẳng trong không gian

I. Khái niệm mở đầu

1. Mặt phẳng

(ảnh 1) (ảnh 2)

Hình ảnh mặt phẳng trong thực tiễn

- Biểu diễn một mặt phẳng: Người ta thường biểu diễn mặt phẳng bằng một hình bình hành.

(ảnh 3)

- Để kí hiệu mặt phẳng ta dùng chữ cái in hoa đặt trong dấu ngoặc ( ).

2. Điểm thuộc mặt phẳng

(ảnh 4)

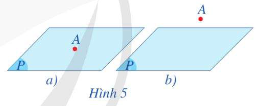
- Điểm A thuộc mặt phẳng (P), ta kí hiệu $A \in (P)$

- Điểm A không thuộc mặt phẳng (P) ta kí hiệu $A \notin (P)$ .

3. Hình biểu diễn của một hình trong không gian

a, Khái niệm

Hình được vẽ trong mặt phẳng để giúp ta hình dung được về một hình trong không gian gọi là hình biểu diễn của hình không gian đó.

b, Quy tắc vẽ hình biểu diễn của một hình trong không gian

- Đường thẳng được biểu diễn bởi đường thẳng, đoạn thẳng được biểu diễn bởi đoạn thẳng.

- Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi 2 đường thẳng song song (hoặc cắt nhau).

- Hình biểu diễn giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.

- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn để biểu diễn cho đường bị che khuất.

II. Các tính chất thừa nhận của hình học không gian

- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.

- Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.

- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu $d \subset (P)$ hoặc $(P) \supset d$ .

- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.

- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu $d = (P) \cap (Q)$ .

- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.

III. Một số cách xác định mặt phẳng

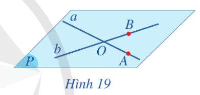
Cho điểm $A \notin d$ . Khi đó qua điểm A và đường thẳng d có một và chỉ một mặt phẳng. Kí hiệu mp(A,d) hoặc (A,d).

(ảnh 5)

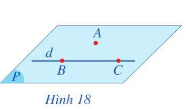
Cho hai đường thẳng a và b cắt nhau. Khi đó, qua a và b có một và chỉ một mặt phẳng, kí hiệu mp(a,b).

(ảnh 6)

IV. Hình chóp và hình tứ diện

1. Hình chóp

- Trong mặt phẳng (P), cho đa giác $A_{1} A_{2} . . . A_{n}$ $(n \geq 3)$ . Lấy điểm S nằm ngoài mặt phẳng (P). Nối S với các đỉnh $A_{1}, A_{2}, . . ., A_{n}$ để được n tam giác $S A_{1} A_{2}, S A_{2} A_{3}, . . ., S A_{n} A_{1}$ . Hình gồm đa giác $A_{1} A_{2} . . . A_{n}$ và n tam giác $S A_{1} A_{2}, S A_{2} A_{3}, . . ., S A_{n} A_{1}$ được gọi là hình chóp và kí hiệu là $S . A_{1} A_{2} . . . A_{n}$ .

- Trong hình chóp $S . A_{1} A_{2} . . . A_{n}$ :

+ Điểm S được gọi là đỉnh.

+ Đa giác $A_{1} A_{2} . . . A_{n}$ được gọi là mặt đáy.

+ Các tam giác $S A_{1} A_{2}, S A_{2} A_{3}, . . ., S A_{n} A_{1}$ được gọi là các mặt bên

+ Các cạnh $S A_{1}, S A_{2}, . . ., S A_{n}$ được gọi là cạnh bên; các cạnh $A_{1} A_{2}, A_{2} A_{3} . . ., A_{n} A_{1}$ được gọi là các cạnh đáy.

Nếu đáy của hình chóp là một tam giác, tứ giác, ngũ giác,…thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,…

2. Hình tứ diện

Cho 4 điểm A, B, C, D không đồng phẳng. Hình gồm 4 tam giác ABC, ABD, ACD và BCD được gọi là hình tứ diện, kí hiệu là ABCD.

(ảnh 7)

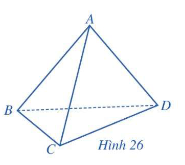
Trong đó, các điểm A, B, C, D được gọi các đỉnh của tứ diện, các đoạn thẳng AB, BC, CD, DA, BD,AC được gọi là cạnh của tứ diện; các tam giác ABC, ABD, ACD và BCD gọi là mặt của tứ diện.

Hai cạnh không có đỉnh chung được gọi là hai cạnh đối diện, đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.