Với giải Bài 4 trang 94 SBT Toán lớp 11 Cánh diều chi tiết trong Bài 1: Đường thẳng và mặt phằng trong không gian giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 1: Đường thẳng và mặt phằng trong không gian
Bài 4 trang 94 SBT Toán 11: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, C, D không cùng nằm trong một mặt phẳng.
Lời giải:
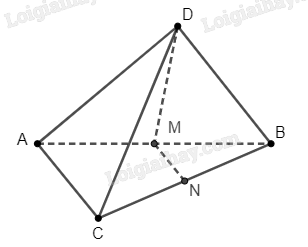
Do là trung điểm của , nên 4 điểm , , , cùng nằm trong mặt phẳng.
Giả sử 4 điểm , , , cùng nằm trong một mặt phẳng.
Điều này có nghĩa là .
Do bốn điểm , , , cùng nằm trong mặt phẳng, ta suy ra .
Điểm và điểm cùng nằm trong mặt phẳng , nên .
Mặt khác, do là trung điểm của , nên .
Suy ra . Điều này là vô lí do là tứ diện nên bốn điểm , , , không cùng nằm trong một mặt phẳng.
Xem thêm lời giải sách bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 6 trang 95 SBT Toán 11: Cho tứ diện . Trên các cạnh lần lượt lấy các điểm sao cho ...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
