Sách bài tập Toán 8 Bài 1 (Chân trời sáng tạo): Đơn thức và đa thức nhiều biến

Admin Vietjack Ngày: 23-09-2024 Lớp 8

2.8 K

Với giải sách bài tập Toán 8 Bài 1: Đơn thức và đa thức nhiều biến sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 1: Đơn thức và đa thức nhiều biến

Giải SBT Toán 8 trang 7

Bài 1 trang 7 SBT Toán 8 Tập 1: Trong các biểu thức sau, biểu thức nào là đơn thức?

$- 2 x^{2} y z; \frac{- 2}{5}; \frac{1}{2} (3 + x^{2}); \frac{1}{x y}; x y z x y z; \sqrt{2} x^{2} y$ .

Lời giải:

Các biểu thức là đơn thức là: $- 2 x^{2} y z; \frac{- 2}{5}; x y z x y z; \sqrt{2} x^{2} y$

Bài 2 trang 7 SBT Toán 8 Tập 1: Lập bốn biểu thức có các biến x, y, trong đó hai biểu thức là đơn thức, hai biểu thức không phải là đơn thức.

Lời giải:

Hai biểu thức là đơn thức gồm 2 biến x, y là: $x y; x^{2} y^{2}$ .

Hai biểu thức không là đơn thức gồm 2 biến x, y là: $x y - 1; x^{2} - y^{2}$ .

Bài 3 trang 7 SBT Toán 8 Tập 1: Hãy sắp xếp các đơn thức sau thành nhóm các đơn thức đồng dạng với nhau.

Lời giải:

Ta có: $- 10 y x^{2} = - 10 x^{2} y$ ; $- \frac{2}{5} z x^{2} y = - \frac{2}{5} x^{2} y z$ ; $0, 25 y^{2} x = 0, 25 x y^{2}$

Do đó, các nhóm đơn thức đồng dạng với nhau là:

Nhóm 1: $2 x^{2} y; - 10 y x^{2}$

Nhóm 2: $- x^{2} y z; - \frac{2}{5} z x^{2} y$

Nhóm 3: $\frac{1}{3} x y^{2}; 0, 25 y^{2} x$

Bài 4 trang 7 SBT Toán 8 Tập 1: Cho bốn ví dụ về đơn thức bậc 3, có các biến là x, y.

Lời giải:

Bốn ví dụ về đơn thức bậc 3, có các biến x, y là: $3 x y^{2}; \frac{1}{3} x^{2} y; - 2 x y^{2}; \frac{- 6}{5} x^{2} y$ .

Bài 5 trang 7 SBT Toán 8 Tập 1: Trong các biểu thức sau, biểu thức nào là đa thức?

$a^{4} - 2 a^{2} + 1; \frac{1}{2} a h; \frac{x}{x - 2};$ $2 a b + \sqrt{2} b c - \frac{1}{3} a c; π^{2} r; x y z + \frac{1}{x y z}$

Lời giải:

Các biểu thức là đa thức là: $a^{4} - 2 a^{2} + 1; \frac{1}{2} a h; 2 a b + \sqrt{2} b c - \frac{1}{3} a c; π^{2} r$

Bài 6 trang 7 SBT Toán 8 Tập 1: Thu gọn và tìm bậc của mỗi đơn thức sau:

a) $2 a^{2} b (- 2) a b$ ;

b) $- \frac{1}{4} b^{2} c a (1 \frac{1}{2}) a b$ ;

c) $0, 2 a b^{3} c .0, 5 b a c^{2}$ .

Lời giải:

a) $2 a^{2} b (- 2) a b = [2. (- 2)] . (a^{2} . a) (b . b) = - 4 a^{3} b^{2}$ ; đơn thức này có bậc 5;

$- \frac{1}{4} b^{2} c a (1 \frac{1}{2}) a b = [\frac{- 1}{4} . \frac{3}{2}] (a . a) (b^{2} . b) . c = \frac{- 3}{8} a^{2} b^{3} c$ ;

đơn thức này có bậc 6;

$0, 2 a b^{3} c .0, 5 b a c^{2} = (0, 2.0, 5) (a . a) (b^{3} . b) (c . c^{2}) = 0, 1 a^{2} b^{4} c^{3}$ ;

đơn thức này có bậc 9.

Bài 7 trang 7 SBT Toán 8 Tập 1: Thu gọn và tìm bậc của mỗi đa thức sau:

a) $6 x - 3 y - 4 x - y + 3 x - 1$ ;

b) $3 x^{2} y + 2 x y^{2} - 3 x y^{2} - 2 x^{2} y$ ;

c) $x^{2} y z - \frac{1}{2} z y x^{2} + \frac{1}{2} y x z^{2}$ ;

d) $- 2 x y x + 6 y x^{2} y + 5 x^{2} y - 4 x^{2} y^{2} - 5 x y^{2} x$ .

Lời giải:

$6 x - 3 y - 4 x - y + 3 x - 1 = (6 x - 4 x + 3 x) + (- 3 y - y) - 1 = 5 x - 4 y - 1$ ; đa thức này có bậc 1.

$3 x^{2} y + 2 x y^{2} - 3 x y^{2} - 2 x^{2} y = (3 x^{2} y - 2 x^{2} y) + (2 x y^{2} - 3 x y^{2}) = x^{2} y - x y^{2}$ ;

đa thức này có bậc 3.

$x^{2} y z - \frac{1}{2} z y x^{2} + \frac{1}{2} y x z^{2} = (x^{2} y z - \frac{1}{2} x^{2} y z) + \frac{1}{2} y x z^{2} = \frac{1}{2} x^{2} y z + \frac{1}{2} x y z^{2}$ ;

đa thức này có bậc 4.

d) $- 2 x y x + 6 y x^{2} y + 5 x^{2} y - 4 x^{2} y^{2} - 5 x y^{2} x$

$= - 2 x^{2} y + 6 x^{2} y^{2} + 5 x^{2} y - 4 x^{2} y^{2} - 5 x^{2} y^{2}$

$= (- 2 x^{2} y + 5 x^{2} y) + (6 x^{2} y^{2} - 4 x^{2} y^{2} - 5 x^{2} y^{2})$

$= 3 x^{2} y - 3 x^{2} y^{2}$

Đa thức này có bậc 4.

Bài 8 trang 7 SBT Toán 8 Tập 1: Tính giá trị của đa thức:

a) $2 a^{2} + 3 a + 2 a b - 2 a^{2} + 2 a - a b$ tại $a = \frac{2}{5}$ và $b = - \frac{1}{2}$ ;

b) $4 a^{2} b - b - a^{3} b^{2} + a .6 a b + a b^{2} a^{2}$ tại $a = - 2$ và $b = 5$ .

Lời giải:

a) Ta có:

$2 a^{2} + 3 a + 2 a b - 2 a^{2} + 2 a - a b = (2 a^{2} - 2 a^{2}) + (3 a + 2 a) + (2 a b - a b) = 5 a + a b$

Với $a = \frac{2}{5}$ và $b = - \frac{1}{2}$ ta có: $5. \frac{2}{5} + \frac{2}{5} . \frac{- 1}{2} = 2 - \frac{1}{5} = \frac{9}{5}$

b) Ta có:

$4 a^{2} b - b - a^{3} b^{2} + a .6 a b + a b^{2} a^{2} = 4 a^{2} b - b - a^{3} b^{2} + 6 a^{2} b + a^{3} b^{2}$

$= (4 a^{2} b + 6 a^{2} b) - b + (a^{3} b^{2} - a^{3} b^{2}) = 10 a^{2} b - b$

Với $a = - 2$ và $b = 5$ ta có: $10. {(- 2)}^{2} .5 - 5 = 200 - 5 = 195$

Bài 9 trang 7 SBT Toán 8 Tập 1: Cho ba hình chữ nhật A, B, C với các kích thước như Hình 1. Tính diện tích của mỗi hình chữ nhật này và tổng diện tích của chúng.

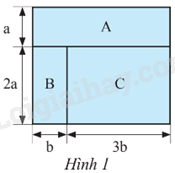
Sách bài tập Toán 8 Bài 1 (Chân trời sáng tạo): Đơn thức và đa thức nhiều biến (ảnh 1)

Lời giải:

Hình chữ nhật A có hai kích thước là a và $b + 3 b = 4 b$ nên diện tích của hình chữ nhật A là: $4 a b$

Hình chữ nhật B có hai kích thước là 2a và b nên diện tích của hình chữ nhật B là: $2 a b$

Hình chữ nhật C có hai kích thước là 2a và 3b nên diện tích của hình chữ nhật C là: $2 a .3 b = 6 a b$

Tổng diện tích của ba hình chữ nhật A, B, C là: $4 a b + 2 a b + 6 a b = 12 a b$

Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Đơn thức và đa thức nhiều biến

Bài 2: Các phép toán với đa thức nhiều biến

Bài 3: Hằng đẳng thức đáng nhớ

Bài 4: Phân tích đa thức thành nhân tử

Bài 5: Phân thức đại số

Bài 6: Cộng, trừ phân thức

Lý thuyết Đơn thức và đa thức nhiều biến

1. Đơn thức

Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.

Ví dụ: $1; 2 x y; - \frac{3}{4} x^{2} y (- 4 x); . . .$ là các đơn thức.

Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến chỉ xuất hiện một lần dưới dạng nâng lên lũy thừa với số mũ nguyên dương.

Ví dụ:

$1; 2 x y; 5 x^{2} y^{4} z; . . .$ là các đơn thức thu gọn.

$3 x^{2} y x; - \frac{3}{4} x^{2} y (- 4 x); . . .$ không phải là các đơn thức thu gọn.

Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.

Ví dụ: đơn thức $3 x^{3} . y$ có hệ số là 3, phần biến là $x^{3} . y$ .

Tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọi là bậc của đơn thức đó.

Chú ý: + Số thực khác 0 là đơn thức bậc không.

+ Số 0 được gọi là đơn thức không có bậc.

Ví dụ: $2 x y$ có bậc là $1 + 1 = 2$

$5 x^{2} y^{4} z$ có bậc là $2 + 4 + 1 = 7$

Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.

Ví dụ:

Hai đơn thức $5 x^{2} y^{4} z$ và $- \frac{1}{3} x^{2} y^{4} z$ có hệ số khác 0 và có cùng phần biến nên chúng là hai đơn thức đồng dạng.

Hai đơn thức $5 x^{2} y^{4} z$ và $5 x y^{2} z$ không có cùng phần biến nên chúng không phải là hai đơn thức đồng dạng.

Cộng, trừ các đơn thức đồng dạng như thế nào?

Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.

Ví dụ:

$\begin{array}{l} 2 x^{3} y^{2} + 4 x^{3} y^{2} = 6 x^{3} y^{2} \\ 4 a y^{2} - 3 a y^{2} = a y^{2} \end{array}$

2. Đa thức

Đa thức là một tổng của những đơn thức.

Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).

Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.

Ví dụ: $x^{2} - 4 x + 3; x^{2} + 3 x y z^{2} - y z + 1; (x + 3 y) + (2 x - - y)$ là đa thức.

$\frac{x + y}{x - y}, \frac{x^{2} + 2}{x^{2} - y^{2}}$ không phải là đa thức.

$x^{2} - 4 x + 3$ có 3 hạng tử.

$x^{2} + 3 x y z^{2} - y z + 1$ có 4 hạng tử.

Đa thức thu gọn là gì?

Đa thức thu gọn là đa thức không chưa hai hạng tử nào đồng dạng.

Thu gọn đa thức như thế nào?

Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.

Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.

Ví dụ:

$\begin{array}{l} A = x^{3} - 2 x^{2} y - x^{2} y + 3 x y^{2} - y^{3} \\ = x^{3} - 3 x^{2} y - 3 x y^{2} - y^{3} \end{array}$

Chú ý: Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.

Tính giá trị của đa thức như thế nào?

Để tính giá trị của một đa thức tại những giá trị cho trước của các biến, ta thay những giá trị cho trước đó vào biểu thức xác định đa thức rồi thực hiện phép tính.

Ví dụ: Giá trị của biểu thức $x^{2} - 4 x y + 3 y^{2}$ tại x = 2, y = 1 là: $2^{2} - 4.2.1 + {3.1}^{2} = - 1$