Với giải Bài 9 trang 103 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 5 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài tập cuối chương 5
Bài 9 trang 103 Toán lớp 10: Một chiếc máy bay được biết là đang bay về phía bắc với tốc độ 45 m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc 20° về phía tây bắc (Hình 2). Tính tốc độ của gió.
Phương pháp giải:
Bước 1: Dựa vào hình 2 xác định các vectơ tương ứng với vận tốc của máy bay, vận tốc so với mặt đất
Bước 2: Dựa vào mối liên hệ giữa các vectơ đã cho xác định vectơ tương ứng với vận tốc gió
Bước 3: Áp dụng định lý cosin tìm tốc độ của gió
Lời giải:
Từ giả thiết ta có:
+) Vectơ tương ứng với vận tốc máy bay là vectơ
+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ
+) Vectơ tương ứng với vận tốc gió là vectơ
Ta có :
Áp dụng định lý cosin ta có:
(m/s)
Vậy tốc độ của gió gần bằng 16 m/s
Bài tập vận dụng:
Bài 1. Cho hình chữ nhật ABCD. Gọi M là trung điểm đoạn BC.
a) Gọi tên các vectơ cùng hướng với .
b) Gọi tên các vectơ ngược hướng với .
c) Chỉ ra các cặp vectơ bằng nhau và đối nhau có các điểm đầu hoặc điểm cuối là A, B, C, D, M.
Hướng dẫn giải
 a) Vectơ-không cùng phương, cùng hướng với mọi vectơ nên cùng hướng với .
a) Vectơ-không cùng phương, cùng hướng với mọi vectơ nên cùng hướng với .
Các vectơ cùng hướng với vectơ và khác là các vectơ có giá song song hoặc trùng với và có hướng từ trên xuống dưới giống như .
Các vectơ thỏa mãn 2 điều kiện trên là: .
Vậy có 4 vectơ thỏa mãn yêu cầu bài toán là: .
b) Vì vectơ-không cùng phương, cùng hướng với mọi vectơ nên vectơ đối của vectơ-không ngược hướng với .
Vectơ đối của vectơ-không là chính nó nên ngược hướng với vectơ .
Các vectơ ngược hướng với là các vectơ có giá song song hoặc trùng với và có hướng ngược lại với , nghĩa là các vectơ cần tìm có hướng dưới lên trên.
Các vectơ thỏa mãn 2 điều kiện trên là: .
Vậy có 5 vectơ thỏa mãn yêu cầu bài toán là: .
c) - Vì ABCD là hình chữ nhật nên AB // CD và AB = CD (tính chất hình chữ nhật)
Mà hai vectơ cùng hướng và hai vectơ cùng hướng.
Do đó và .
+ Tương tự ta có: và
+ M là trung điểm của BC nên BM = MC =
Mà hai vectơ cùng hướng và hai vectơ cúng hướng.
Do đó và
- và là hai vectơ cùng độ dài nhưng ngược hướng nên
Do đó và là hai vectơ đối nhau.
Tương tự ta có các cặp vectơ đối nhau là: và ; và và ; và và
Bài 2. Một con thuyền trôi theo hướng nam vận tốc 25 km/h, dòng nước chảy theo hướng đông với vận tốc 10 km/h. Tính độ dài vectơ tổng của hai vectơ nói trên (làm tròn kết quả đến hàng trăm).
Hướng dẫn giải
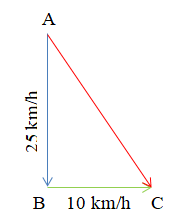
Gọi A là vị trí con thuyền xuất phát.
Vận tốc của con thuyền được biểu diễn bởi .
Vận tốc của dòng nước được biểu diễn bởi .
Khi đó ta có vectơ tổng của hai vectơ nói trên là .
Do đó độ lớn của vectơ cần tìm là:.
Vì con thuyền trôi theo hướng nam và dòng nước chảy theo hướng đông.
Nên ta có AB ⊥ BC.
Ta có độ lớn vận tốc con thuyền là 25 km/h.
Suy ra = AB = 25.
Ta có độ lớn vận tốc dòng nước là 10 km/h.
Suy ra = BC = 10.
Tam giác ABC vuông tại B: AC2 = AB2 + BC2 (Định lý Py ‒ ta ‒ go)
⇔ AC2 = 252 + 102 = 725.
⇒ AC = ≈ 26,93.
Vậy độ dài vectơ tổng của hai vectơ nói đến trong bài xấp xỉ bằng 26,93 (km/h).
Bài 3. Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị theo hai vecto và
Hướng dẫn giải
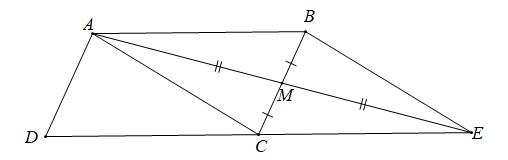
Gọi E là điểm đối xứng với A qua M.
Khi đó M là trung điểm của BC và AE.
Suy ra tứ giác ABEC là hình bình hành.
(quy tắc hình bình hành)
Mà (M là trung điểm của AE)
Xét hình bình hành ABCD có: (quy tắc hình bình hành)
Vậy
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 102 Toán lớp 10: Cho ba vectơ đều khác vectơ . Các khẳng định sau đúng hay sai?...
Bài 6 trang 103 Toán lớp 10: Cho . So sánh độ dài, phương và hướng của hai vectơ và ...
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Tích vô hướng của hai vecto
Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu