Phương pháp giải và bài tập về Đường phân giác trong tam giác chọn lọc

Quý Lê Xuân Ngày: 08-03-2024 Lớp 7

Tải xuống 2 2.2 K 8

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Cách giải đường phân giác trong tam giác Toán lớp 7, tài liệu bao gồm 2 trang, tuyển chọn bài tập Cách giải đường phân giác trong tam giác có phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Cách giải đường phân giác trong tam giác gồm các nội dung chính sau:

A. Phương phương giải

- tóm tắt lý thuyết ngắn gọn.

B. Bài tập

- gồm 10 bài tập tự luyện giúp học sinh tự rèn luyện Cách giải đường phân giác trong tam giác.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Cách giải đường phân giác trong tam giác (ảnh 1)

ĐƯỜNG PHÂN GIÁC TRONG TAM GIÁC

A. Phương pháp giải

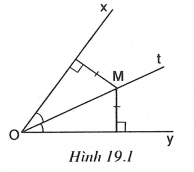
1. Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó (h.19.1).

2. Đảo lại, điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

3. Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó (h.19.2).

4. Trong một tam giác, hai đường phân giác của hai góc ngoài và đường phân giác của góc trong không kề cùng đi qua một điểm (h.19.3).

Cách giải đường phân giác trong tam giác (ảnh 2)

B. Bài tập

Câu 1. Cho $Δ A B C$ có $A = 100^{o};$ Hai đường phân giác BM và CN của tam giác cắt nhau tại E. Tính số đo của góc $\hat{B E C} .$

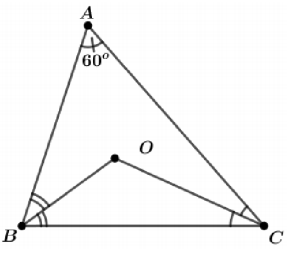
Câu 2. Cho hình vẽ bên, tính $\hat{B O C} .$

Câu 3. Cho $Δ A B C$ vuông tại A; BM là đường phân giác. Vẽ $M H ⊥ B C; M H$ cắt AB tại E. Chứng minh:

a) $Δ A B M = Δ H B M .$

b) So sánh: AM và CM.

c) $B M ⊥ E C .$

Câu 4. Cho $Δ A B C$ đường cao AH, đường phân giác BD và góc $\hat{A H D} = 45^{o} .$ Tính góc $\hat{A D B} .$

Câu 5. Cho $(\hat{A} = 90^{o});$ BD là phân giác của góc B $(D \in A C) .$ Trên tia BC lấy điểm E sao cho BA=BE.

a) Chứng minh BD là đường trung trực của AE.

b) Kẻ $A H ⊥ B C .$ So sánh EH và EC.

Câu 6. Cho tam giác ABC. Chứng minh rằng hai đường phân giác ngoài của góc B và góc C cùng với đường phân giác trong góc A đồng quy.

Câu 7. Cho góc $x O y$ . Lấy điểm A trên Ox, lấy điểm B trên Oy. Vẽ các tia phân giác của các góc $B A x$ và $A B y$ cắt nhau tại M. Từ M vẽ một đường thẳng vuông góc với OM cắt Ox,Oy tại C và D. Chứng minh tam giác OCD cân.

Câu 8. Cho tam giác ABC có $\hat{B} = 120^{0}$ , phân giác BD và CE. Đường thẳng chứa tia phân giác ngoài tại đỉnh A của tam giác ABC cắt đường thẳng BC tại F. Chứng minh rằng $\hat{A D F} = \hat{B D F}$ và D,E,F thẳng hàng.

Câu 9. Cho tam giác ABC, các tia phân giác góc B và C cắt nhau tại O. Từ A vẽ đường thẳng vuông góc với OA cắt các tia BO và CO lần lượt tại M và N. Chứng minh $B M ⊥ B N$ và $C M ⊥ C N$ .

Câu 10. Cho tam giác ABC, $\hat{B} = 45^{0}$ , đường cao AH, phân giác BD. Cho biết $\hat{B D A} = 45^{0}$ . Chứng minh rằng $H D / / A B$ .

Xem thêm

Trang 1

Trang 2

Tài liệu có 2 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm