Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Tính chất tia phân giác của một góc. Tính chất ba đường phân giác của tam giác Toán lớp 7, tài liệu bao gồm 11 trang, tuyển chọn bài tập Tính chất tia phân giác của một góc. Tính chất ba đường phân giác của tam giác đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Tính chất tia phân giác của một góc. Tính chất ba đường phân giác của tam giác gồm các nội dung chính sau:

A. Phương pháp giải

- tóm tắt lý thuyết ngắn gọn.

B. Một số ví dụ

- gồm 2 ví dụ minh họa đa dạng của các dạng bài tập Tính chất tia phân giác của một góc. Tính chất ba đường phân giác của tam giác có lời giải chi tiết.

C. Bài tập vận dụng

- gồm 14 bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng bài tập Tính chất tia phân giác của một góc. Tính chất ba đường phân giác của tam giác.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

TÍNH CHẤT TIA PHÂN GIÁC CỦA MỘT GÓC. TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

A. Phương pháp giải

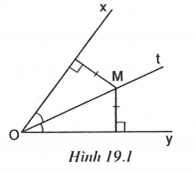
1. Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó (h.19.1).

2. Đảo lại, điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

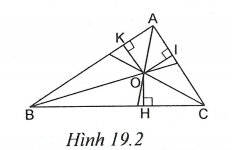
3. Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó (h.19.2).

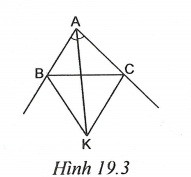
4. Trong một tam giác, hai đường phân giác của hai góc ngoài và đường phân giác của góc trong không kề cùng đi qua một điểm (h.19.3).

B. Một số ví dụ

Ví dụ 1. Cho tam giác ABC cân tại A. Trên nửa mặt phẳng bờ AC không chứa B vẽ tia $Ax//BC.$ Lấy điểm O trên tia Ax, điểm M trên AB và điểm N trên AC sao cho $\widehat{AMO}=\widehat{ANO}.$ Chứng minh rằng  là tam giác cân.

Giải (h.19.4)

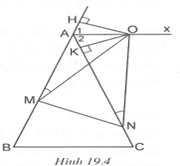
* Tìm cách giải.

Ta có $Ax//BC$ nên dễ thấy Ax là tia phân giác của góc ngoài tại đỉnh A của tam giác ABC. Vì điểm O nằm trên tia phân giác này nên ta vẽ $OH\perp AB,OK\perp AC$ để vận dụng tính chất cách đều hai cạnh của điểm O. Từ đó dùng phương pháp tam giác bằng nhau để chứng minh   $OM=ON.$

* Trình bày lời giải.

Ta có $Ax//BC$ nên ${\widehat{A}}_1=\widehat{B}$ (cặp góc đồng vị); ${\widehat{A}}_2=\widehat{C}$ (cặp góc so le trong).

Mặt khác, $\widehat{B}=\widehat{C}$ (hai góc ở đáy của tam giác cân) nên  ${\widehat{A}}_1={\widehat{A}}_2.$

Vẽ $OH\perp AB,OK\perp AC$ ta được $OH=OK$ (tính chất điểm nằm trên tia phân giác).

Ta chứng minh được $\Delta HOM=\Delta KON$ (g.c.g). Suy ra $OM=ON,$ do đó $\Delta OMN$ cân.

Ví dụ 2. Cho tam giác ABC vuông tại $A,AB<AC.$ Trên cạnh AC lấy điểm D sao cho $AD=AB.$ Gọi E là một điểm nằm giữa A và D sao cho tia BD là tia phân giác của góc CBE. Vẽ $EH\perp BC.$ Tính số đo của góc CHD.

Giải (h.19.5)

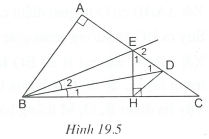
* Tìm cách giải.

Vẽ hình chính xác, ta dự đoán $\widehat{CHD}=45°.$ Do đó cần chứng minh HD là đường phân giác của góc CHE. Muốn vậy phải chứng minh EC là đường phân giác ngoài tại đỉnh E của tam giác EBH. 

* Trình bày lời giải.

Ta có ${\widehat{E}}_1=\widehat{ABC}$ (cùng phụ với góc C). Do đó ${\widehat{E}}_1=\widehat{ABD}+{\widehat{B}}_1.$ (1)

Lại có $\widehat{E_2}=\widehat{D_1}+\widehat{B_2}$ (2) (tính chất góc ngoài của  $\Delta EBD).$

Mặt khác, $\widehat{ABD}=\widehat{D_1}\left(=45°\right)$ và ${\widehat{B}}_1={\widehat{B}}_2$ nên  ${\widehat{E}}_1={\widehat{E}}_2.$

Xét $\Delta EBH$ có D là giao điểm của đường phân giác góc B với đường phân giác góc ngoài tại đỉnh E nên HD là đường phân giác góc ngoài tại đỉnh H.

Suy ra  $\widehat{CHD}=90°:2=45°.$

Vi dụ 3. Cho tam giác ABC vuông tại A. Vẽ $AH\perp BC.$ Tia phân giác của góc HAC cắt BC tại K. Các đường phân giác của góc BAH và góc BHA cắt nhau tại O. Gọi M là trung điểm của AK. Chứng minh ba điểm B, O, M thẳng hàng.