Thực hành 1 trang 46 Toán 11 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 46 Toán 11 Tập 1 Chân trời sáng tạo | Giải bài tập Toán lớp 11

Van Anh Ngày: 17-06-2023 Lớp 11

259

Với giải Thực hành 1 trang 46 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Dãy số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 1: Dãy số

Thực hành 1 trang 46 Toán 11 Tập 1: Cho dãy số:

u: N* $\to$ R

n $\mapsto$ u_n = n³.

a) Hãy cho biết dãy số trên là hữu hạn hay vô hạn.

b) Viết năm số hạng đầu tiên của dãy số đã cho.

Lời giải:

a) Dãy số trên là dãy số vô hạn.

b) Năm số hạng đầu tiên của dãy số đã cho là:

u(1) = 1³ = 1;

u(2) = 2³ = 8;

u(3) = 3³ = 27;

u(4) = 4³ = 64;

u(5) = 5³ = 125.

Video bài giảng Toán 11 Bài 1: Dãy số - Chân trời sáng tạo

Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 45 Toán 11 Tập 1:.....

Hoạt động khám phá 1 trang 45 Toán 11 Tập 1: Cho hàm số:.....

Hoạt động khám phá 2 trang 46 Toán 11 Tập 1: Cho hàm số:.....

Thực hành 1 trang 46 Toán 11 Tập 1: Cho dãy số:....

Vận dụng 1 trang 46 Toán 11 Tập 1: Cho 5 hình tròn theo thứ tự có bán kính 1; 2; 3; 4; 5.....

Hoạt động khám phá 3 trang 46 Toán 11 Tập 1: Cho các dãy số (a_n), (b_n), (c_n), (d_n) được xác định như sau:....

Thực hành 2 trang 47 Toán 11 Tập 1: Cho dãy số (u_n) xác định bởi: ......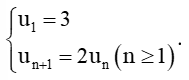

Vận dụng 2 trang 47 Toán 11 Tập 1: Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1 cột dỗ (Hình 1). Gọi u_n là số cột gỗ nằm ở lớp thứ n tính từ trên xuống và cho biết lớp trên cùng có 14 cột gỗ. Hãy xác định dãy số (u_n) bằng hai cách:.....

Hoạt động khám phá 4 trang 48 Toán 11 Tập 1: Cho hai dãy số (a_n) và (b_n) được xác định như sau: a_n = 3n + 1, b_n = – 5n.......

Thực hành 3 trang 48 Toán 11 Tập 1: Xét tính tăng, giảm của các dãy số sau:......

Vận dụng 3 trang 49 Toán 11 Tập 1: Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp nhau hơn kém nhau 1 cột gỗ (Hình 2)......

Hoạt động khám phá 5 trang 49 Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{1}{n}$ . So sánh các số hạng của dãy số với 0 và 1.......

Thực hành 4 trang 49 Toán 11 Tập 1: Xét tính bị chặn của các dãy số sau.....

Bài 1 trang 50 Toán 11 Tập 1: Tìm u₂, u₃ và dự đoán công thức số hạng tổng quát của u_n dãy số: .....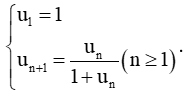

Bài 2 trang 50 Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{1}{1.2} + \frac{1}{2.3} + ... + \frac{1}{n (n + 1)}$ . Tìm u₁, u₂, u₃ và dự đoán công thức số hạng tổng quát của u_n......

Bài 3 trang 50 Toán 11 Tập 1: Xét tính tăng, giảm của dãy số (y_n) với $y_{n} = \sqrt{n + 1} - \sqrt{n}$ .....

Bài 4 trang 50 Toán 11 Tập 1: Xét tính bị chặn của các dãy số sau:....

Bài 5 trang 50 Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{2 n - 1}{n + 1}$ . Chứng minh (u_n) là dãy số tăng và bị chặn.....

Bài 6 trang 50 Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{n a + 2}{n + 1}$ . Tìm các giá trị của a để:....

Bài 7 trang 50 Toán 11 Tập 1: Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đó từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?.....

Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân

Bài tập cuối chương 2

Từ khóa :

Toán 11

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 5

Thay .?. bằng hỗn số có chứa phân số thập phân thích hợp. Trong khay có .?. cái bánh Lữ Ngọc My My

Toán Lớp 5

Viết các số đo dưới dạng hỗn số. Mẫu: 612 dm = 61(2/10) m Lữ Ngọc My My

Toán Lớp 5

Chọn các phân số thập phân và hỗn số bằng nhau. 3 258/10; 3 258/100; 3 258/1000 Lữ Ngọc My My

Toán Lớp 5

Viết các phân số thập phân ở dạng hỗn số. Mẫu: 37/10 = 3(7/10) Lữ Ngọc My My

Tìm kiếm