Với giải Bài 4 trang 38 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 2: Hệ bất phương trình bậc nhất hai ẩn học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Bài 4 trang 38 Toán lớp 10: Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mỗi loại để có được nhiều tiền nhất.
Phương pháp giải:
Bước 1: Lập các điều kiện ràng buộc đối với x, y thành hệ bất phương trình.
Bước 2: Biểu diễn miền nghiệm của mỗi bất phương trình trên cùng hệ trục tọa độ Oxy.
Lời giải:
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên x≥0,y≥0
- Tổng số giờ vẽ không quá 30 giờ nên 2x+3y≤30
- Số tấm thiệp tối thiểu là 12 tấm nên
Từ đó ta có hệ bất phương trình:
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.

Miền không gạch chéo (miền tam giác ABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có:
Tính giá trị của F tại các đỉnh của tam giác:
Tại
Tại
Tại
F đạt giá trị lớn nhất bằng 180 tại
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất.
Bài tập vận dụng:
Bài 1. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
a)
b)
c) y – 2x < 0
d)
Hướng dẫn giải
- Hệ bất phương trình là hệ bất phương trình bậc nhất hai ẩn vì có hai bất phương trình x < 1 và y - 1 > 2 đều là bất phương trình bậc nhất hai ẩn.
- Hệ bất phương trình không là hệ bất phương trình bậc nhất hai ẩn vì có bất phương trình x2 + y < 0 không là bất phương trình bậc nhất hai ẩn.
- y – 2x < 0 không là hệ bất phương trình bậc nhất hai ẩn vì chỉ có một bất phương trình bậc nhất hai ẩn.
Hệ bất phương trình là hệ bất phương trình bậc nhất hai ẩn vì có hai bất phương trình 2x – y < 5 và 4x + 3y > 1010 đều là bất phương trình bậc nhất hai ẩn.
Vậy có hệ và là hệ bất phương trình bậc nhất hai ẩn.
Bài 2. Cho hệ bất phương trình . Hỏi đây có phải hệ bất phương trình bậc nhất hai ẩn không? Khi cho y = 0, x có thể nhận các giá trị nguyên nào?
Hướng dẫn giải
là hệ bất phương trình bậc nhất hai ẩn bởi vì có 2 bất phương trình x + 5y < 1 và 5x – 4y > 6 là bất phương trình bậc nhất hai ẩn.
Khi y = 0, hệ trở thành: (vô lí)
Vậy không có giá trị nguyên nào của x thoả mãn để y = 0.
Bài 3. Cho hệ bất phương trình
a) Tìm hai nghiệm của hệ trên.
b) Cho F (x; y) = 2x + 2y. Tìm giá trị lớn nhất của F (x; y).
Hướng dẫn giải
a) Chọn (x; y) = (1; 1).
Thay x = 1 và y = 1 vào bất phương trình x ≥ 0 ta được 1 ≥ 0 là mệnh đề đúng. Do đó cặp (1; 1) là nghiệm của bất phương trình x ≥ 0.
Thay x = 1 và y = 1 vào bất phương trình y ≥ 0 ta được 1 ≥ 0 là mệnh đề đúng. Do đó cặp (1; 1) là nghiệm của bất phương trình y ≥ 0.
Thay x = 1 và y = 1 vào bất phương trình x + y ≤ 80 ta được 1 + 1 = 2 ≤ 80 là mệnh đề đúng. Do đó cặp (1; 1) là nghiệm của bất phương trình x + y ≤ 80.
Thay x = 1 và y = 1 vào bất phương trình 2x + y ≤ 120 ta được 2. 1 + 1 = 3 ≤ 120 là mệnh đề đúng. Do đó cặp (1; 1) là nghiệm của bất phương trình 2x + y ≤ 120.
Vậy (x; y) = (1; 1) là nghiệm của hệ bất phương trình .
Tương tự ta chọn được (x; y) = (2; 2) là nghiệm của hệ bất phương trình.
Vậy hai cặp số (1; 1), (2; 2) là nghiệm của hệ bất phương trình.
b)
- Xác định miền nghiệm D1 của bất phương trình x ≥ 0.
+ Đường thẳng x = 0 là trục tọa độ Oy.
+ Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy (kể cả trục Oy) nằm bên phải trục Oy.
- Tương tự, miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox (kể cả trục Ox) nằm bên trên trục Ox.
- Miền nghiệm D3 của bất phương trình x + y ≤ 80:
+ Vẽ đường thẳng d1: x + y = 80.
+ Xét gốc toạ độ O(0; 0) có: 0 + 0 = 0 ≤ 80 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 80.
Do đó, miền nghiệm D3 của bất phương trình x + y ≤ 80 là nửa mặt phẳng bờ d1 (kể cả bờ d1) chứa gốc tọa độ O.
- Miền nghiệm D4 của bất phương trình 2x + y ≤ 120:
+ Vẽ đường thẳng d2: 2x + y = 120.
+ Xét gốc toạ độ O(0; 0) có: 2. 0 + 0 = 0 ≤ 120 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình 2x + y ≤ 120.
Do đó, miền nghiệm D4 của bất phương trình 2x + y ≤ 120 là nửa mặt phẳng bờ d2 (kể cả bờ d2) chứa gốc tọa độ O.
Từ đó ta có miền nghiệm không bị gạch là giao miền nghiệm của các bất phương trình trong hệ.
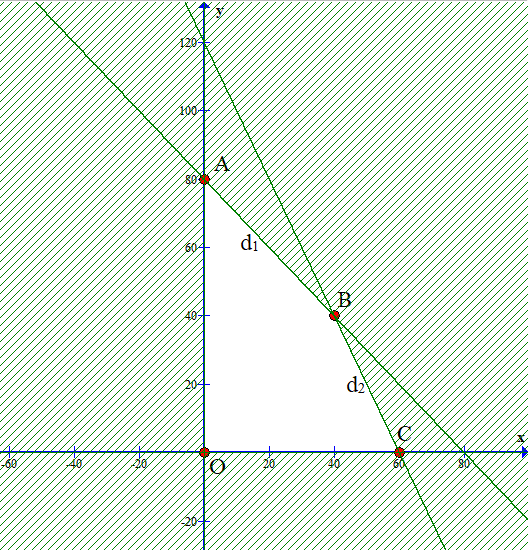
Miền nghiệm của hệ bất phương trình trên là miền tứ giác OABC với:
O(0; 0), A(0; 80), B(40; 40), C(60; 0).
Tại O(0; 0): F = 2.0 + 2.0 = 0;
Tại A(0; 80): F = 2.0 + 2.80 = 160;
Tại B(40; 40): F = 2.40 + 2.40 = 160;
Tại C(60; 0): F = 2.60 + 2.0 = 120;
Vậy giá trị lớn nhất của F (x; y) là 160 khi (x; y) = (0; 80) hoặc (x; y) = (40, 40).
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 34 Toán lớp 10: Hãy chỉ ra hai nghiệm của mỗi hệ bất phương trình trong Ví dụ 1...
Thực hành 2 trang 35 Toán lớp 10: Biểu diễn miền nghiệm của hệ bất phương trình:...
Bài 1 trang 37 Toán lớp 10: Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau:...
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Bất phương trình bậc nhất hai ẩn
Bài 2: Hệ bất phương trình bậc nhất hai ẩn