Với giải Bài 10 trang 120 Toán lớp 7 Cánh diều chi tiết trong Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài tập cuối chương 7
Bài 10 trang 120 Toán 7 Tập 2: Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 145). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ D đến điểm A là nhỏ nhất? Em hãy giúp bạn Hùng tìm cách vẽ điểm D và giải thích cách làm của mình.
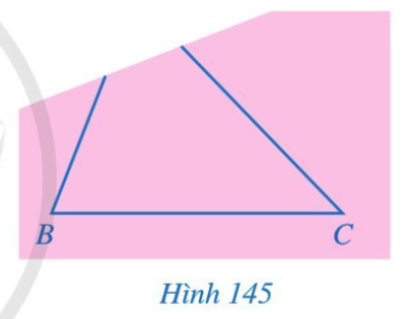
Lời giải:
Để tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ D đến điểm A là nhỏ nhất thì AD là nhỏ nhất.
Khi đó theo tính chất đường xiên và đường vuông góc kẻ từ một điểm đến một đường thẳng, ta thấy DA nhỏ nhất khi AD là đường vuông góc kẻ từ D tới BC (tức là AD BC) hay D là chân đường vuông góc kẻ từ A đến BC.
Ta xác định điểm D như sau:
Bước 1. Kẻ hai đường cao xuất phát từ đỉnh B và đỉnh C của tam giác ABC.
Bước 2. Gọi H là giao điểm của hai đường cao xuất phát từ đỉnh B và đỉnh C của tam giác ABC.
Khi đó H chính là trực tâm của tam giác ABC.
Suy ra đường cao AD của tam giác ABC đi qua điểm H.
Do đó HD BC tại D.
Bước 3. Từ H kẻ đường vuông góc với BC, cắt BC tại một điểm.
Điểm này chính là điểm D cần tìm.
Ta có hình vẽ sau:
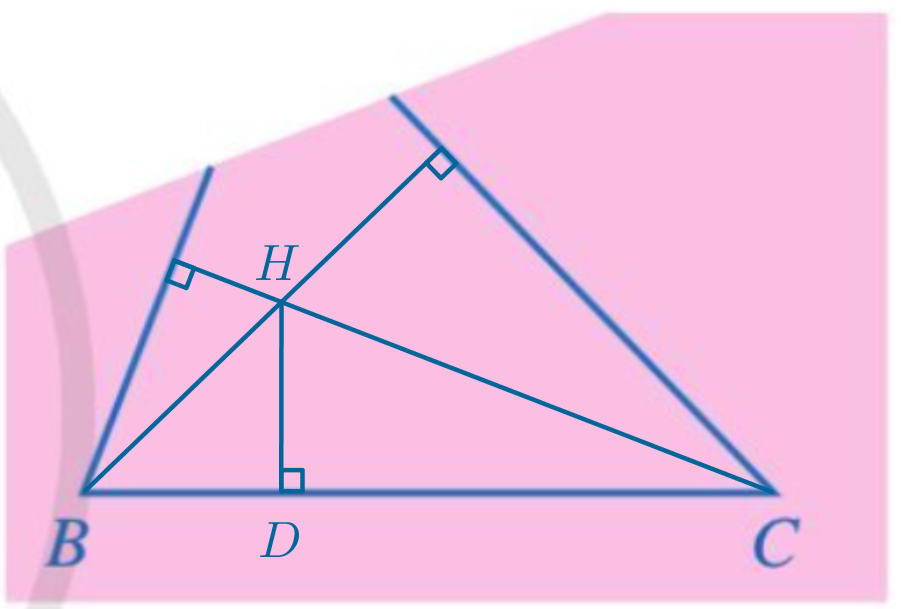
Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 1 trang 119 Toán 7 Tập 2: Cho tam giác ABC có: ...
Bài 2 trang 119 Toán 7 Tập 2: Tìm các số đo x, y trong Hình 140...
Bài 3 trang 119 Toán 7 Tập 2: Bạn Hoa đánh dấu ba vị trí A, B, C trên một phần sơ đồ xe buýt ở Hà Nội năm 2021 và xem xe buýt có thể đi như thế nào giữa hai vị trí A và B. Đường thứ nhất đi từ A đến C và đi tiếp từ C đến B, đường thứ hai đi từ B đến A (Hình 141). Theo em, đường nào đi dài hơn? Vì sao?...
Bài 4 trang 119 Toán 7 Tập 2: Cho hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh: AI = MK...
Bài 5 trang 119 Toán 7 Tập 2: Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N....
Bài 6 trang 119 Toán 7 Tập 2: Cho tam giác ABC cân tại A có...
Bài 7 trang 119 Toán 7 Tập 2: Cho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng hàng. Hai đường cao BM và CN của tam giác ABC cắt nhau tại I, hai đường cao CP và DQ của tam giác ECD cắt nhau tại K (Hình 143). Chứng minh AI // EK....
Bài 8 trang 120 Toán 7 Tập 2: Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144)....
Bài 9 trang 120 Toán 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:...
Bài 10 trang 120 Toán 7 Tập 2: Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 145). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ D đến điểm A là nhỏ nhất? Em hãy giúp bạn Hùng tìm cách vẽ điểm D và giải thích cách làm của mình....
Bài 11 trang 120 Toán 7 Tập 2: Cho tam giác MNP có Khi đó bằng:...
Bài 12 trang 120 Toán 7 Tập 2: Cho tam giác nhọn MNP có trực tâm H. Khi đó, góc HMN bằng góc nào sau đây?...
Bài 13 trang 120 Toán 7 Tập 2: Cho tam giác MNP có MN = 1 dm, NP = 2 dm, MP = x dm với x ∈ {1; 2; 3; 4}. Khi đó, x nhận giá trị nào?...
Bài 14 trang 120 Toán 7 Tập 2: Nếu tam giác MNP có trọng tâm G, đường trung tuyến MI thì tỉ số bằng...
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:
Giải SGK Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác
Giải SGK Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác
Giải SGK Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác
Giải SGK Toán 7 Bài 13: Tính chất ba đường cao của tam giác
Giải SGK Toán 7: Bài tập cuối chương 7

