Với giải Bài 9 trang 120 Toán lớp 7 Cánh diều chi tiết trong Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài tập cuối chương 7

Bài 9 trang 120 Toán 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:

a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng.

b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.

Lời giải:

a)

Chứng minh (Hình vẽ dưới đây):

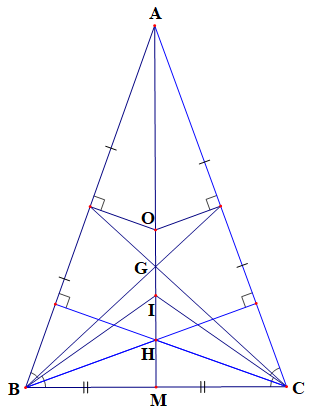
+) Gọi M là trung điểm của BC.

Khi đó AM là đường trung tuyến của $∆$ABC.

Lại có G là trọng tâm của tam giác ABC (giả thiết) nên đường trung tuyến AM đi qua trọng tâm G của tam giác.

Do đó A, G, M thẳng hàng (1).

+) Vì M là trung điểm của BC nên MB = MC.

Do tam giác ABC cân tại A (giả thiết) nên AB = AC và $\widehat{ABC}=\widehat{ACB}$.

Xét $∆$AMB và $∆$AMC có:

AK là cạnh chung,

MB = MC (chứng minh trên),

AB = AC (chứng minh trên),

Do đó $∆$AMB = $∆$AMC (c.c.c).

Suy ra $\widehat{AMB}=\widehat{AMC}$ (hai góc tương ứng)

Mà $\widehat{AMB}+\widehat{AMC}=180°$ (hai góc kề bù) nên $\widehat{AMB}=\widehat{AMC}=\frac{180°}{2}=90°$.

Do đó AM $\perp$ BC hay AM là đường cao kẻ từ đỉnh A của tam giác ABC.

Mặt khác H là trực tâm của tam giác ABC (giả thiết) nên đường cao AM đi qua trực tâm H của tam giác.

Do đó A, H, M thẳng hàng (2).

+) Vì O là giao điểm ba đường trung trực của tam giác ABC nên OA = OB = OC.

Xét $∆$OBM và $∆$OCM có:

OK là cạnh chung,

OB = OC (chứng minh trên),

MB = MC (chứng minh trên),

Do đó $∆$OBM = $∆$OCM (c.c.c).

Suy ra $\widehat{OMB}=\widehat{OMC}$ (hai góc tương ứng)

Mà $\widehat{OMB}+\widehat{OMC}=180°$ (hai góc kề bù) nên $\widehat{OMB}=\widehat{OMC}=\frac{180°}{2}=90°$.

Do đó OK $\perp$ BC.

Lại có AM $\perp$ BC (chứng minh trên)

Suy ra A, O, M thẳng hàng (3).

+) Do BI là tia phân giác của $\widehat{ABC}$ nên $\widehat{IBC}=\frac{1}{2}\widehat{ABC}$.

Do CI là tia phân giác của $\widehat{ACB}$ nên $\widehat{ICB}=\frac{1}{2}\widehat{ACB}$.

Mà $\widehat{ABC}=\widehat{ACB}$ (chứng minh trên) nên $\widehat{IBC}=\widehat{ICB}$ 

Tam giác IBC có $\widehat{IBC}=\widehat{ICB}$ nên tam giác IBC cân tại I, do đó IB = IC.

Xét $∆$IBM và $∆$ICM có:

IB = IC (chứng minh trên),

$\widehat{IBM}=\widehat{ICM}$ (do $\widehat{IBC}=\widehat{ICB}$),

MB = MC (chứng minh trên),

Do đó $∆$IBM = $∆$ICM (c.g.c).

Suy ra $\widehat{IMB}=\widehat{IMC}$(hai góc tương ứng)

Mà $\widehat{IKB}+\widehat{IKC}=180°$ (hai góc tương ứng) nên $\widehat{IMB}=\widehat{IMC}=\frac{180°}{2}=90°$.

Do đó IM $\perp$ BC.

Lại có AM $\perp$ BC (chứng minh trên)

Suy ra A, I, K thẳng hàng (4).

Từ (1), (2), (3) và (4) ta có A, G, H, I, O thẳng hàng.

Vậy các điểm A, G, H, I, O thẳng hàng khi tam giác ABC cân tại A.

b)

Chứng minh (Hình vẽ dưới đây):

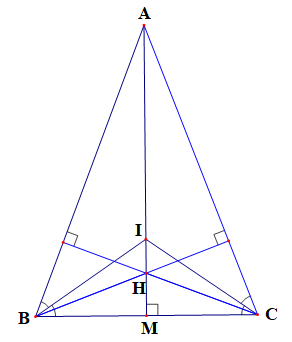
Gọi M là chân đường cao kẻ từ A tới BC.

Do đó AM là đường cao kẻ từ đỉnh A của tam giác ABC.

Mà H là trực tâm của tam giác ABC (giả thiết) nên đường cao AM đi qua điểm H.

Khi đó ba điểm A, H, M thẳng hàng.

Mà A, H, I thẳng hàng (giả thiết) nên A, H, I, K thẳng hàng.

Mà AI là tia phân giác của $\widehat{BAC}$ nên AM là đường phân giác của $\widehat{BAC}$.

Do đó $\widehat{\text{MA}B}=\widehat{\text{MA}C}$.

Xét $∆$ABM (vuông tại M) và $∆$ACM (vuông tại M) có:

$\widehat{\text{MA}B}=\widehat{\text{MA}C}$ (chứng minh trên),

AM là cạnh chung,

Do đó $∆$ABM = $∆$ACM (cạnh góc vuông – góc nhọn kề).

Suy ra AB = AC (hai cạnh tương ứng).

Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.