Với giải Bài 64 trang 87 SBT Toán lớp 7 Cánh diều chi tiết trong Bài 9: Đường trung trực của một đoạn thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 9: Đường trung trực của một đoạn thẳng
Bài 64 trang 87 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A có . Đường trung trực của BC cắt AC tại M. Chứng minh:
a) BM là tia phân giác của góc ABC;
b) MA < MC.
Lời giải:
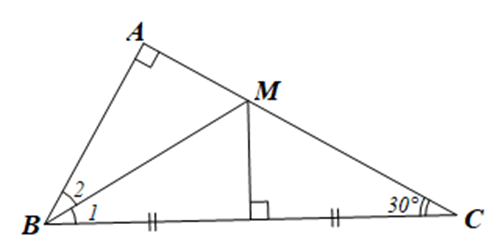
a) Vì DABC vuông tại A nên (trong tam giác vuông, tổng hai góc nhọn bằng 90o).
Suy ra .
Vì điểm M thuộc đường trung trực của BC nên MB = MC.
Do đó tam giác MBC cân ở M.
Suy ra
Mặt khác (hai góc kề nhau)
Nên
Suy ra
Do đó BM là tia phân giác của góc ABC.
Vậy BM là tia phân giác của góc ABC.
b) Trong tam giác vuông ABM có MA < MB (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).
Mà MB = MC (chứng minh câu a).
Suy ra MA < MC.
Vậy MA < MC.
Xem thêm các bài giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 60 trang 87 sách bài tập Toán lớp 7 Tập 2: Xác định điểm M thuộc đường thẳng BC sao cho M cách đều A và B trong mỗi trường hợp sau:....
Bài 61 trang 87 sách bài tập Toán lớp 7 Tập 2: Một con đường liên xã cách không xa hai địa điểm dân cư và hai địa điểm này nằm ở cùng một phía của con đường. Hãy xác định một địa điểm trên con đường đó để xây dựng nhà văn hóa xã sao cho nhà văn hóa đó cách đều hai địa điểm dân cư.....
Bài 62 trang 87 sách bài tập Toán lớp 7 Tập 2: Quan sát Hình 44, biết ∆MAB = ∆NAB. Chứng minh đường thẳng AB là đường trung trực của đoạn thẳng MN.....
Bài 63 trang 87 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có AB < AC. Đường trung trực của đoạn thẳng BC cắt cạnh AC tại M. Chứng minh AM + BM = AC.....
Bài 64 trang 87 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A có . Đường trung trực của BC cắt AC tại M. Chứng minh:....
Bài 65 trang 87 sách bài tập Toán lớp 7 Tập 2: Quan sát Hình 45, biết AM là đường trung trực của đoạn thẳng BC và DB = DC. Chứng minh ba điểm A, M, D thẳng hàng.....
Bài 66 trang 88 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có M là trung điểm BC; ME vuông góc với AB tại E, MF vuông góc với AC tại F. Chứng minh:....
Bài 67 trang 88 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A. Đường trung trực của đoạn thẳng AC cắt cạnh AB tại D. Biết CD là tia phân giác của góc ACB. Tính số đo mỗi góc của tam giác ABC.....
Bài 68 trang 88 sách bài tập Toán lớp 7 Tập 2: Cho góc xOy khác góc bẹt. Oz là tia phân giác của góc đó, M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C. Qua M vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:....
Bài 69 trang 88 sách bài tập Toán lớp 7 Tập 2: Cho góc xOy nhọn. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Đường trung trực của đoạn thẳng OA và đường trung trực của đoạn thẳng OB cắt nhau tại I. Chứng minh:.....
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
SBT Toán 7 Bài 8 : Đường vuông góc và đường xiên
SBT Toán 7 Bài 9 : Đường trung trực của một đoạn thẳng
SBT Toán 7 Bài 10 : Tính chất ba đường trung tuyến của tam giác
SBT Toán 7 Bài 11 : Tính chất ba đường phân giác của tam giác
SBT Toán 7 Bài 12 : Tính chất ba đường trung trực của tam giác