HĐ 3 trang 42 Toán lớp 7: Hãy mô tả lại các bước đã thực hiện trong phép chia đa thức D cho đa thức E

Phương pháp giải:

Mô tả lại các bước tương tự như chia đa thức cho đa thức trường hợp chia hết.

Lời giải:

Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của D chia cho hạng tử bậc cao nhất của E.

Bước 2: Lấy D trừ đi tích của E với thương mới thu được ở bước 1

Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của E

Bước 4: Lấy dư thứ nhất trừ đi tích E với thương vừa thu được ở bước 3. Ta được dư thứ hai có bậc nhỏ hơn bậc của E thì quá trình chia kết thúc.

HĐ 4 trang 42 Toán lớp 7: Kí hiệu dư thứ hai là G = - 6x + 10 . Đa thức này có bậc bằng 1. Lúc này phép chia có thể tiếp tục được không? Vì sao?

Phương pháp giải:

Đa thức bậc n không chia được cho đa thức bậc m (n < m)

Lời giải:

Lúc này phép chia không thực hiện được nữa vì bậc của đa thức -6x + 10 (là 1) nhỏ hơn bậc của đa thức chia x2 + 1 (là 2)

HĐ 5 trang 42 Toán lớp 7: Hãy kiểm tra lại đẳng thức D = E . (5x – 3) + G

Phương pháp giải:

Bước 1: Thực hiện phép nhân đa thức E .(5x – 3)

Bước 2: Thực hiện phép cộng đa thức tìm được ở bước 1 với đa thức G

Nếu kết quả = đa thức D thì đúng

Lời giải:

Ta có: E . (5x – 3) + G

= (x² + 1) . (5x – 3) + (-6x + 10)

= x² .(5x – 3) + 1. (5x – 3) + (-6x) + 10

= x² . 5x + x2 . (-3) + 5x – 3 – 6x + 10

= 5x³ – 3x² + (5x – 6x) + (-3 + 10)

= 5x³ – 3x² – x + 7

= D

Vậy đẳng thức đúng.

Luyện tập 3 trang 42 Toán lớp 7: Tìm dư R và thương Q trong phép chia đa thức A= 3x⁴ – 6x – 5 cho đa thức B = x² + 3x – 1 rồi viết A dưới dạng A = B . Q + R

Phương pháp giải:

+)  Muốn chia đa thức A cho đa thức B, ta làm như sau:

Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.

Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1

Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B

Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3

Bước 5: Làm tương tự như trên

Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.

+) Viết A = B. Q + R

Lời giải:

Vậy A = (x² + 3x – 1) . (3x² – 9x + 30)  -105x + 25

Thử thách nhỏ trang 42 Toán lớp 7: Em có biết tại sao Vuông làm nhanh thế không?

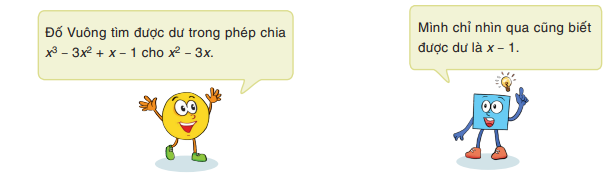
Phương pháp giải:

Xét phép chia (A + B) : C với bậc của B nhỏ hơn bậc của C

Nếu A chia C không dư thì số dư của (A + B) : C là B

Lời giải:

Ta có: x³ – 3x² + x – 1 =  (x³ – 3x²) + (x -1).

Vì x³ – 3x² chia cho x² – 3x không dư ; bậc của x – 1 nhỏ hơn bậc của x² – 3x nên số dư của phép chia (x³ – 3x²) + (x -1) cho x² – 3x là x – 1

Vậy Vuông làm nhanh và đúng.

Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Giải Toán 7 trang 40 Tập 2