Với giải Bài 5 trang 84 Toán lớp 7 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 8 trang 84 giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài tập cuối chương 8 trang 84

Bài 5 trang 84 Toán lớp 7 Tập 2: Cho tam giác ABC nhọn (AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng $\widehat{BMN}=\widehat{HAC}$.

b) Kẻ MI $\perp$AH (I $\in$AH), gọi K là giao điểm của AH với BM. Chứng minh rằng I là trung điểm của AK.

Lời giải:

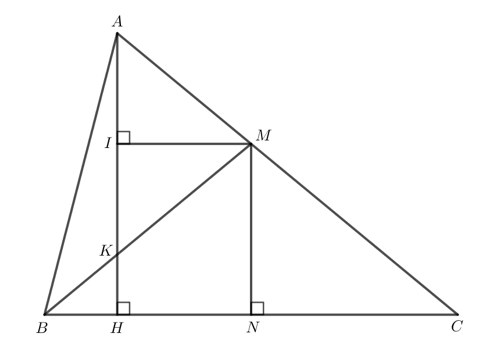
a) Do M nằm trên đường trung trực của BC nên MB = MC.

Xét $\Delta BMN$vuông tại N và $\Delta CMN$vuông tại N có:

MB = MC (chứng minh trên).

MN chung.

Do đó $\Delta BMN=\Delta CMN$(cạnh huyền - cạnh góc vuông).

Suy ra $\widehat{BMN}=\widehat{CMN}$(2 góc tương ứng) (1).

Do MN $\perp$BC, AH $\perp$BC nên MN // AH.

Do đó $\widehat{CMN}=\widehat{HAC}$(2 góc đồng vị) (2).

Từ (1) và (2) suy ra $\widehat{BMN}=\widehat{HAC}$.

b) Do $\Delta BMN=\Delta CMN$(cạnh huyền - cạnh góc vuông) nên $\widehat{MBN}=\widehat{MCN}$(2 góc tương ứng).

Do MI $\perp$AH, BC $\perp$AH nên MI // BC.

Do đó $\widehat{AMI}=\widehat{MCN}$(2 góc đồng vị) và $\widehat{KMI}=\widehat{MBN}$(2 góc so le trong).

Do đó $\widehat{AMI}=\widehat{KMI}$.

Xét $\Delta AMI$vuông tại I và $\Delta KMI$vuông tại I có:

$\widehat{AMI}=\widehat{KMI}$(chứng minh trên).

MI chung.

Do đó $\Delta AMI=\Delta KMI$(góc nhọn - cạnh góc vuông).

Suy ra AI = KI (2 cạnh tương ứng).

Mà I nằm giữa A và K nên I là trung điểm của AK.