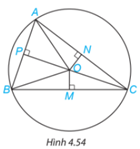
Luyện tập 3 trang 79 Toán lớp 7: Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra ba cặp tam giác vuông bằng nhau trong hình.
Phương pháp giải:
Quan sát hình vẽ và chỉ ra 3 cặp tam giác vuông bằng nhau
Lời giải:
Ba cặp tam giác vuông bằng nhau có trong hình vẽ là:
+ Tam giác OMB và tam giác OMC
+ Tam giác ONA và tam giác ONC
+ Tam giác OPA và tam giác OPB
Thử thách nhỏ trang 79 Toán lớp 7: Có hai chiếc thang dài như nhau được dựa vào một bức tường với cùng độ cao BH = B’H’ như Hình 4.55. Các góc BAH và B'A'H có bằng nhau không? Vì sao?
Phương pháp giải:
Chứng minh hai tam giác BAH và B'A'H’ bằng nhau, từ đó suy ra 2 góc bằng nhau.
Lời giải:
Xét hai tam giác BAH và B'A'H’ có:
AB=A’B’
BH=B’H’
Suy ra ( cạnh huyền – cạnh góc vuông)
=>(hai góc tương ứng).
Bài tập
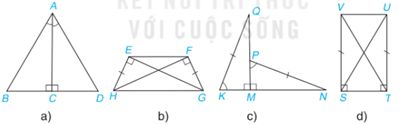
Bài 4.20 trang 79 Toán lớp 7: Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
Phương pháp giải:
Lời giải:
a) Xét 2 tam giác vuông ABC và ADC có:
AC chung
(gt)
=>(g.c.g)
b) Xét 2 tam giác vuông HEG và GFH có:
HE=GF(gt)
HG chung
=>(c.h-c.g.v)
c) Xét 2 tam giác vuông QMK và NMP có:
QK=NP
=>(cạnh huyền – góc nhọn)
d) Xét 2 tam giác vuông VST và UTS có:
VS=UT
ST chung
=>(c.g.c)
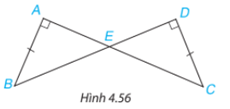
Bài 4.21 trang 79 Toán lớp 7: Cho hình 4.56, biết AB=CD, . Chứng minh rằng .
Phương pháp giải:
Lời giải:
Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AED và DEC có:
(đối đỉnh) và .
Suy ra:
Xét 2 tam giác vuông AEB và DEC có:
AB=DC
=>(g.c.g)
Bài 4.22 trang 79 Toán lớp 7: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng .
Phương pháp giải:
Lời giải:
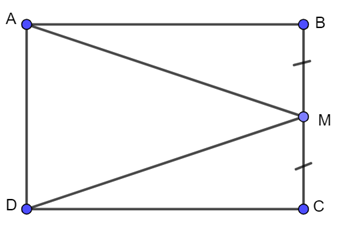
Xét 2 tam giác vuông ABM và DCM có:
AB=DC (tính chất hình chữ nhật)
BM=CM (gt)
=>(c.g.c)
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
