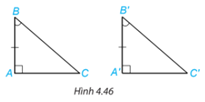
HĐ 2 trang 76 Toán lớp 7: Hai tam giác vuông ABC (vuông tại đỉnh A) và ABC vuông tại đỉnh A) có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB = A'B', (H.4.46). Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
Phương pháp giải:
Chứng minh 2 tam giác bằng nhau theo trường hợp góc - cạnh - góc.
Lời giải:
Xét 2 tam giác ABC và A'B'C' có:
AB=A’B’
(g.c.g)
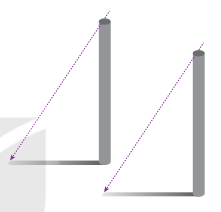
Luyện tập 1 trang 76 Toán lớp 7: Quay lại tình huống mở đầu, ta thấy mỗi chiếc cột với bóng của nó tạo thành hai cạnh góc vuông của một tam giác vuông. Hai tam giác vuông này có hai cặp cạnh tương ứng bằng nhau và hai góc ở đỉnh chiếc cột của hai tam giác vuông này cũng bằng nhau. Vậy lí do mà bạn Tròn đưa ra có đúng không?
Phương pháp giải:
Áp dụng trường hợp bằng nhau của tam giác vuông.
Lời giải:
Lí do mà bạn Tròn đưa ra là đúng. Vì hai tam giác vuông này bằng nhau ( g-c-g)
HĐ 3 trang 76 Toán lớp 7: Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốc bởi các đường thẳng BC, B’C’ và các góc B, B’. Khi đó AC, A’C’ mô tả độ cao của hai con dốc.
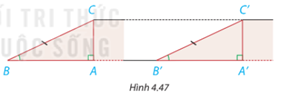
a) Dựa vào trường hợp bằng nhau góc - cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A’B’C’ bằng nhau.
b) So sánh độ cao của hai con dốc.
Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – góc nhọn
b) Chứng minh AC=A’C’
Lời giải:
a)Xét hai tam giác vuông ABC và A’B’C’ có:
BC=B’C’
(cạnh huyền – góc nhọn)
b)Do nên AC=A’C’ ( 2 cạnh tương ứng)
Vậy độ cao hai con dốc bằng nhau.
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác: