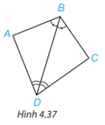
Luyện tập 2 trang 73 Toán lớp 7: Chứng minh hai tam giác ABD và CBD trong hình 4.37 bằng nhau.
Phương pháp giải:
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải:
Xét hai tam giác ABD và CBD có:
BD chung
(g.c.g)
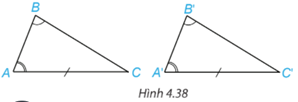
Thử thách nhỏ trang 73 Toán lớp 7: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?
Phương pháp giải:
Kiểm tra xem góc còn lại của hai tam giác có bằng nhau không?
Lời giải:
Do hai tam giác trên có hai cặp cạnh bằng nhau nên cặp góc còn lại bằng nhau.
Vậy hai tam giác đã cho bằng nhau theo trường hợp góc – cạnh – góc.
Bài tập
Bài 4.12 trang 73 Toán lớp 7: Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

Phương pháp giải:
Lời giải:
a)Xét tam giác ABD và tam giác CBD có:
AB=CD
BD chung
Vậy (c.g.c)
b)Xét hai tam giác OAD và OCB có:
AO=CO
(đối đỉnh)
OD=OB
Vậy (c.g.c)
Bài 4.13 trang 73 Toán lớp 7: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.
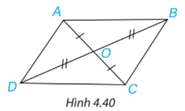
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;
b) Chứng minh rằng DAB = BCD.
Phương pháp giải:
Lời giải:
a) Hai cặp tam giác có chung đỉnh O bằng nhau là: AOB và COD; AOD và COB theo trường hợp cạnh – góc – cạnh.
b)
Do hai tam giác AOD và COB nên: (2 góc tương ứng) và AD=BC (2 cạnh tương ứng)
Xét DAB và BCD có:
AD=BC
BD chung
Vậy DAB =BCD (c.g.c)
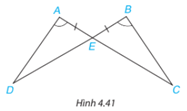
Bài 4.14 trang 73 Toán lớp 7: Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
Phương pháp giải:
Lời giải:
Xét hai tam giác ADE và BCE có:
AE=BE
(đối đỉnh)
Vậy (g.c.g)
Bài 4.15 trang 73 Toán lớp 7: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:
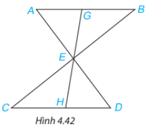
a) ABE =DCE;
b) EG = EH.
Phương pháp giải:
Lời giải:
a)Xét hai tam giác ABE và DCE có:
(so le trong)
AB=CD(gt)
(so le trong)
Vậy ABE =DCE(g.c.g)
b)Xét hai tam giác BEG và CEH có:
(đối đỉnh)
CE=BE (do ABE =DCE)
(so le trong)
Suy ra (g.c.g)
Vậy EG=EH (hai cạnh tương ứng).
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác: