Với tóm tắt lý thuyết Toán lớp 7 Chương 9 sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 7.

Lý thuyết Toán lớp 7 Chương 9

Tổng hợp lý thuyết Toán 7 Chương 9

1. Góc đối diện với cạnh lớn hơn trong một tam giác

Định lí 1: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

2. Cạnh đối diện với góc lớn hơn tỏng một tam giác

Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Nhận xét

+ Trong tam giác vuông, góc vuông là góc lớn nhất nên cạnh đối diện với vuông góc (tức là cạnh huyền) là cạnh lớn nhất.

3. Khái niệm đường vuông góc và đường xiên

Từ một điểm A không nằm trên đường thẳng d, kẻ đường thẳng vuông góc với d tại H. Lấy một điểm M trên d (M khác H), kẻ đoạn thẳng AM.

Trong hình trên đây:

+ Đoạn thẳng AH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d.

+ H là chân đường vuông góc hạ từ A xuống d.

+ Đoạn thẳng AM là một đường xiên kẻ từ A đến đường thẳng d.

4. Quan hệ giữa đường vuông góc và đường xiên

Định lí: Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.

Chú ý: Vì độ dài đoạn thẳng AH là ngắn nhất trong các đoạn thẳng kẻ từ A đến d nên độ dài đoạn thẳng AH được gọi là khoảng cách từ điểm A đến đường thẳng d.

5. Bất đẳng thức tam giác

Định lí: Trong một tam giác, độ dài của một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại.

Cho tam giác ABC như hình dưới đây:

Ta suy ra được các hệ thức sau:

AB < AC + BC

AC < AB + BC

BC < AC + AB

Ba hệ thức phai trên được gọi là các bất đẳng thức tam giác.

6. Quan hệ giữa ba cạnh của một tam giác

Từ định lí trên, ta suy ra được tinh chất sau:

Tính chất: Trong một tam giác, độ dài của một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại.

Nhận xét: Với a, b, c là độ dài ba cạnh tùy ý của một tam giác thì từ định lí và tinh chất nêu trên ta có:

b – c < a < b + c

Chú ý: Để kiểm tra ba độ dài có là ba cạnh của một tam giác hay không, ta chỉ cần so sanh độ dài lớn nhất có nhỏ hơn tổng hai độ dài còn lại hoặc độ dài nhỏ nhất có lớn hơn hiệu hai độ dài còn lại hay không.

7. Sự đồng quy của ba đường trung tuyến trong một tam giác

a) Đường trung tuyến của tam giác

Trong hình dưới đây, đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC.

b) Sự đồng quy của ba đường trung tuyến

Định lí 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm đó cách mổi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

Chú ý: Điểm đồng quy của ba đường trung tuyến gọi là trọng tâm tam giác.

8. Sự đồng quy của ba đường phân giác trong tam giác

a) Đường phân giác của tam giác

Trong hình dưới đây, cho tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D thì đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.

b) Sự đồng quy của ba đường phân giác

Định lí 2: Ba đường phân giác của một tam giác đồng quy tại một điểm. Điểm này cách đều ba cạnh của tam giác đó.

9. Sự đồng quy của ba đường trung trực trong một tam giác

a) Đường trung trực của tam giác

Trong tam giác ABC, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác. Ở hình dưới đây, a là đường trung trực ứng với cạnh BC của tam giác ABC.

b) Sự đồng quy của ba đường trung trực

Định lí 1: Ba đường trung trực của một tam giác đồng quy tại một điểm. Điểm này cách đều ba đỉnh của tam giác.

Nhận xét: Vì giao điểm O của ba đường trung trực trong tam giác ABC cách đều ba đỉnh của tam giác đó (OA = OB = OC) nên có một đường tròn tâm O đi qua ba đỉnh A, B, C.

9. Sự đồng quy của ba đường cao trong tam giác

a) Đường cao của tam giác

Trong hình dưới đây, đoạn thẳng AH kẻ từ đỉnh A, vuông góc với cạnh đối diện BC là một đường cao của tam giác ABC. Ta còn nói AH là đường cao xuất phát từ đỉnh A (hay đường cao ứng với cạnh BC).

b) Sự đồng quy của ba đường cao

Định lí 2: Ba đường cao của một tam giác đồng quy tại một điểm.

Chú ý:

- Điểm đồng quy của ba đường cao của một tam giác gọi là trực tâm của tam giác đó.

- Gọi H là trực tâm của tam giác ABC, ta có:

+) Khi ABC là tam giác nhọn thì H nằm bên trong tam giác.

+) Khi ABC là tam giác vuông thì H trùng với A (kí hiệu H ≡ A).

+) Khi ABC là tam giác tù thì H nằm bên ngoài tam giác.

Bài tập Tổng hợp Toán 7 Chương 9

Bài 1: Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng 60º.

Hướng dẫn giải

Xét tam giác ABC có BC là cạnh lớn nhất và góc đối diện của cạnh BC là $\hat{A}$ .

Theo định lí 1, ta có $\hat{A}$ là góc lớn nhất thỏa mãn: $\hat{A}\ge \hat{B},\hat{A}\ge \hat{C}$ .

Suy ra $\hat{A}+\hat{A}+\hat{A}\ge \hat{A}+\hat{B}+\hat{C}$

Hay $3\hat{A}\ge \hat{A}+\hat{B}+\hat{C}$

Do đó $\hat{A}\ge \frac{\hat{A}+\hat{B}+\hat{C}}{3}=\frac{180°}{3}=60°$ .

Vậy suy ra số đo góc A lớn hơn hoặc bằng 60º (đpcm).

Bài 2: Cho tam giác ABC cân tại A, hai điểm D, E nằm trên đường thẳng BC, D nằm giữa B và C, C nằm giữa D và E. Hãy chứng minh AD < AC < AE.

Hướng dẫn giải

Do trong một tam giác cân, hai góc của đáy luôn bé hơn 90º nên suy ra $\widehat{ACB}$là góc nhọn.

Mà $\widehat{ACE}$kề bù với $\widehat{ACB}$nên suy ra $\widehat{ACE}$là góc tù.

Xét tam giác ACE có $\widehat{ACE}$là góc tù nên cạnh đối diện với $\widehat{ACE}$là cạnh AE là cạnh lớn nhất.

Suy ra AE > AC (*)

Mà tam giác ABC cân tại A nên AB = AC và $\widehat{ABC}=\widehat{ACB}$.

Lại có:

∙ Xét tam giác ABC có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$

Suy ra $\widehat{BAC}=180°-2\widehat{ABC}$(1)

∙ Xét tam giác ABD có: $\widehat{BAD}+\widehat{ABD}+\widehat{ADB}=180°$

Suy ra $\widehat{BAD}=180°-\widehat{ABD}-\widehat{ADB}$(2)

Mà D nằm giữa B và C nên suy ra $\widehat{BAD}<\widehat{BAC}$(3)

Từ (1), (2) và (3) ta suy ra được:

$180°-\widehat{ABD}-\widehat{ADB}<180°-2\widehat{ABC}$

Hay $\widehat{ABC}+\widehat{ADB}>2\widehat{ABC}$.

Do đó $\widehat{ADB}>\widehat{ABC}$.

Áp dụng định lí 2 ta được: AB > AD.

Mà AB = AC (cmt) nên suy ra AC > AD (**)

Từ (*) và (**) nên suy ra AE > AC > AD (đpcm).

Bài 3: Hãy giải thích tại sao trong tam giác tù, cạnh đối diện góc tù là cạnh lớn nhất.

Hướng dẫn giải

Giả sử tam giác ABC là tam giác tù tại đỉnh A nên suy ra $90°<\hat{A}<180°$(1)

Lại có tam giác ABC có tổng ba góc trong tam giác bằng 180º nên suy ra:

$\hat{A}+\hat{B}+\hat{C}=180°$

Do đó $\hat{A}=180°-\left(\hat{B}+\hat{C}\right)$.

Do đó với $90°<180°-\left(\hat{B}+\hat{C}\right)<180°$thì $0°<\hat{B}+\hat{C}<90°$.

Hay ta suy ra được $0°<\hat{B}<90°$ và $0°<\hat{C}<90°$ (2)

Từ (1) và (2) ta có: $\hat{A}>\hat{B},\hat{A}>\hat{C}$.

Theo định lí 2, ta có: BC > AC và BC > AB nên BC là cạnh lớn nhất.

Vậy trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất (đpcm).

Bài 4: Cho tam giác ABC cân tại A. Chứng minh rằng khoảng cách từ B đến đường thẳng AC bằng khoảng cách từ C đến đường thẳng AB.

Hướng dẫn giải

Kẻ BD $\perp$ AC; CE $\perp$ AB (D $\in$ AC, E $\in$ AB).

Xét ∆ADB và ∆AEC có:

$\hat{A}$ chung

$\widehat{ADB}=\widehat{AEC}\left(=90°\right)$

AB = AC (do tam giác ABC cân tại A).

Do đó ∆ADB = ∆AEC (cạnh huyền – góc nhọn).

Suy ra BD = CE (hai cạnh tương ứng) (đpcm).

Bài 5: Cho hai điểm phân biệt A, B ở cùng phía đối với đường thẳng d (A, B không thuộc d). Chứng minh rằng nếu A, B có cùng khoảng cách đến đường thẳng d thì AB song song với d.

Hướng dẫn giải

Kẻ AC, BD vuông góc với d nên suy ra được AC // BD.

Suy ra $\widehat{CAD}=\widehat{BDA}$(hai góc ở vị trí so le trong)

Theo giả thiết ta có: AC = BD

Xét ∆ACD và ∆DBA có:

AD là cạnh chung

$\widehat{CAD}=\widehat{BDA}$(cmt)

AC = BD (giả thiết)

Do đó ∆ACD = ∆DBA (g.c.g).

Suy ra $\widehat{ADC}=\widehat{DAB}$(hai góc tương ứng)

Mà $\widehat{ADC}$và $\widehat{DAB}$ở vị trí so le trong.

Do đó AB // CD hay AB // d (đpcm).

Bài 6: Cho tam giác ABC cân tại A và một điểm M thuộc đoạn thẳng BC, M khác B và C. Chứng minh rằng tổng khoảng cách từ điểm M đến các đường thẳng AB, AC là một số không đổi.

Hướng dẫn giải

Gọi BG và CH là đường cao kẻ từ B và C của tam giác ABC.

Gọi MD, ME lần lượt là khoảng cách từ M đến AB và AC.

Kẻ MF song song với cạnh AC (F thuộc AB)

MF giao với BG tại điểm I.

Tương tự cách làm của Bài 1 thì ta dễ dàng suy ra được: BG = CH (4)

Tổng khoảng cách từ M đến AB và AC là MD + ME (1)

Ta có:

+) BG và ME cùng vuông góc với AC nên suy ra ME // BG hay ME // IG

Lại có: MF song song với AC hay MI // EG

Nên suy ra MIGE là hình chữ nhật. Từ đó ta có ME = IG (2)

+) Tam giác FBM cân tại F do hai góc B và M bằng nhau.

Với MD là khoảng cách từ M đến FB và BI là khoảng cách từ điểm B đến FM.

Chứng minh tương tự Bài 1, ta dễ dàng suy ra được MD = BI (3)

Từ (1), (2), (3), (4) nên suy ra: MD + ME = BI + IG = BG = CH.

Vậy suy ra tổng khoảng cách từ M đến AB và AC chính bằng khoảng cách từ C đến AB nên không đổi (đpcm).

Bài 7: Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.

Hướng dẫn giải

+) Xét tam giác ABD, áp dụng định lí ta có:

AD < AB + BD (1)

+) Xét tam giác ADC , áp dụng định lí ta có:

AD < AC + DC (2)

Cộng vế với vế của (1) và (2) ta có:

2AD < (AB + BD) + (AC + CD)

Hay 2AF < AB + (BD + CD) + AC

Suy ra 2AF < AB + BC + AC

Tương đương với $AF<\frac{AB+BC+AC}{2}$

Mà $\frac{AB+BC+AC}{2}$ là nửa chu vi tam giác ABC.

Vậy suy ra AD nhỏ hơn nửa chu vi tam giác ABC (đpcm).

Bài 8: Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC. So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB.

Hướng dẫn giải

+) Xét tam giác BMN, áp dụng định lí ta có:

MB < MN + NB

Từ đó suy ra MA + MB < MA + MN + NB.

Do đó MA + MB < (MA + MN) + NB = NA + NB.

Vậy MA + MB < NA + NB (đpcm).

Bài 9: Cho tam giác ABC có AB = 1 và BC = 7. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên.

Hướng dẫn giải

Xét tam giác ABC:

+) Theo định lí ta có: AC < AB + BC = 1 + 7 = 8 (1)

+) Theo tinh chất ta có: AC > BC – AB = 7 – 1 = 6 (2)

Từ (1) và (2) suy ra 6 < AC < 8.

Mà độ dài cạnh AC là một số nguyên nên suy ra AC = 7.

Bài 10: Gọi M là trung điểm của cạnh BC của tam giác ABC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm của AB cắt BC tại U, đường thẳng qua D và trung điểm của AC cắt BC tại V. Chứng minh BU = UV = VC.

Hướng dẫn giải

+) Tam giác BAC có M là trung điểm của BC nên suy ra MB = MC (1)

+) Xét tam giác ABD có U là giao của 2 đường trung tuyến BM và DE nên U là trọng tâm tam giác ABD.

Áp dụng định lí 1 ta có: $\frac{BU}{MB}=\frac{2}{3}\Rightarrow BU=\frac{2}{3}MB$ (2)

Từ đó ta có: $UM=BM-BU=MB-\frac{2}{3}MB=\frac{1}{3}MB$ (3)

+) Xét tam giác ACD có V là giao của 2 đường trung tuyến CM và DF nên V là trọng tâm tam giác AVD

Áp dụng định lí 1 ta có: $\frac{VC}{MC}=\frac{2}{3}\Rightarrow VC=\frac{2}{3}MC$ (4)

Từ đó ta có: $MV=CM-VC=MC-\frac{2}{3}MC=\frac{1}{3}MC$ (5)

Từ (1), (3), (5) ta có:

$UV=UM+MV=\frac{1}{3}MB+\frac{1}{3}MC=\frac{2}{3}MB$ (6)

Từ (1), (2), (4), (6) ta có: $BU=UV=VC=\frac{2}{3}MB$ .

Vậy BU = UV = VC (đpcm).

Bài 11: Tam giác ABC có AD, BE là hai đường phân giác và $\widehat{BAC}=120°$ . Chứng minh rằng DE là tia phân giác của góc ADC.

Hướng dẫn giải

Gọi Ax là tia đối của tia AB thì ba góc BAD, DAC, CAx có cùng số đo 60º.

Hạ EH ⏊ Bx, EI ⏊ AD, EK ⏊ BC

Ta có: Vì BE là phân giác góc ABC nên suy ra EH = EK (Áp dụng định lí 2)

Vì AE là phân giác góc DAx nên suy ra EH = EI (Áp dụng định lí 2)

Suy ra EK = EI hay E nằm trên tia phân giác của ADC

Vậy suy ra DE là đường phân giác của góc ADC (đpcm).

Bài 12: Cho tam giác ABC với M là trung điểm của BC. Lấy điểm N sao cho C là trung điểm của đoạn thẳng BN. Lấy điểm P sao cho M là trung điểm của đoạn thẳng AP. Chứng minh đường thẳng AC đi qua trung điểm của PN, đường thẳng PC đi qua trung điểm của AN.

Hướng dẫn giải

Trong tam giác ANP có đường trung tuyến NM và NC = BC = 2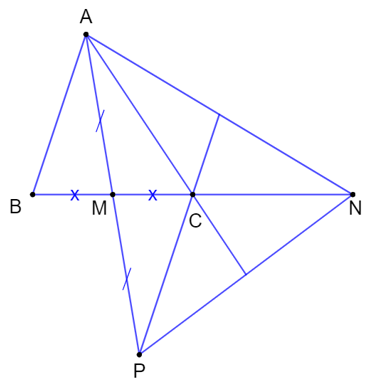CM nên C là trọng tâm của tam giác ANP.

Vậy AC, PC là hai đường tung tuyến của tam giác ANP

Vì thế suy ra AC đi qua trung điểm của PN và PC đi qua trung điểm của AN.

Bài 13: Cho tam giác ABC vuông. Kẻ đường thẳng vuông góc với cạnh huyền BC của tam giác ABC tại điểm D không thuộc đoạn BC. Nó cắt đường thẳng chứa cạnh AB tại E và cắt đường thẳng chứa cạnh AC tại F. Xác định trực tâm của tam giác BEF.

Hướng dẫn giải

Trong tam giác BEF, đường cao xuất phát từ B là đường thẳng BD, đường cao xuất phát từ F là đường thẳng FA.

Hai đường cao BD và FA cắt nhau tại C.

Vậy suy ra C là trực tâm của tam giác BEF.

Bài 14: Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S. Chứng minh tia PO là tia phân giác của góc RPS.

Hướng dẫn giải

Tam giác OPM là tam giác cân tại O (Vì Ox là đường trung trực của đoạn thẳng PM)

Suy ra $\widehat{OPM}=\widehat{OMP}$ (1) và OM = OP.

Lại có tam giác RPM là tam giác cân tại R (Vì Ox, hay chính là Rx là đường trung trực của đoạn thẳng PM).

Suy ra $\widehat{RPM}=\widehat{RMP}$ (2)

Trừ vế với vế của (1) cho (2) ta có:

$\widehat{OPM}-\widehat{RPM}=\widehat{OMP}-\widehat{RMP}$

Hay $\widehat{OPR}=\widehat{OMR}$(*)

Tương tự ta có tam giác OPN là tam giác cân tại O (Vì Oy là đường trung trực của đoạn thẳng PN)

Suy ra $\widehat{OPN}=\widehat{ONP}$ (3) và ON = OP.

Lại có tam giác SPN là tam giác cân tại R (Vì Oy, hay chính là Sy là đường trung trực của đoạn thẳng PN).

Suy ra $\widehat{SPN}=\widehat{SNP}$ (4)

Trừ vế với vế của (3) cho (4) ta có:

$\widehat{OPN}-\widehat{SPN}=\widehat{ONP}-\widehat{SNP}$.

Hay $\widehat{OPS}=\widehat{ONS}$(**)

Vì OM = ON (= OP) nên tam giác OMN là tam giác cân tại O.

Do đó: $\widehat{OMR}=\widehat{ONS}$(***)

Từ (*), (**), (***) ta suy ra được $\widehat{OPR}=\widehat{OPS}$.

Vậy suy ra PO là tia phân giác của góc RPS (đpcm).

Bài 15: Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh $\widehat{BAC}=45°$.

Hướng dẫn giải

Gọi BJ là đường cao xuất phát từ B của tam giác ABC.

Xét hai tam giác AHJ và tam giác BCJ có:

AH = BC (gt)

$\widehat{AJH}=\widehat{BJC}\left(=90°\right)$

$\widehat{JAH}=\widehat{JBC}$(cùng phụ với $\widehat{JCB}$)

Do đó ∆AHJ = ∆BCJ (cạnh huyền – góc nhọn)

Suy ra AJ = BJ (hai cạnh tương ứng)

Xét tam giác JAB vuông tại J và có AJ = BJ (cmt)

Nên JAB là tam giác vuông cân tại J.

Vậy $\widehat{BAJ}=\widehat{BAC}=45°$(đpcm).

Xem thêm các bài tóm tắt lý thuyết Toán 7 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác

Lý thuyết Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Lý thuyết Chương 9: Quan hệ giữa các yếu tố trong một tam giác

Lý thuyết Bài 36: Hình hộp chữ nhật và hình lập phương

Lý thuyết Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

Lý thuyết Chương 10: Một số hình khối trong thực tiễn