Với giải Bài 8 trang 100 SGK Toán lớp 10 Cánh diều chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài tập cuối chương 4

Bài 8 trang 100 Toán lớp 10: Cho hình bình hành ABCD có AB = 4, AD = 6, $\widehat{BAD}=60°$ (Hình 74).

a) Biểu thị các vectơ $\overrightarrow{BD},\overrightarrow{AC}$ theo $\overrightarrow{AB},\overrightarrow{AD}$. 

b) Tính các tích vô hướng $\overrightarrow{AB}.\overrightarrow{AD},\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{BD}.\overrightarrow{AC}$. 

c) Tính độ dài các đường chéo BD, AC. 

Lời giải:

a) Ta có: $\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}$. 

Do ABCD là hình bình hành nên $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$. 

b) Ta có: $\overrightarrow{AB}.\overrightarrow{AD}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AD}\right|.\cos \left(\overrightarrow{AB},\overrightarrow{AD}\right)$

$=AB.AD.\cos \widehat{BAD}$ = 4 . 6 . cos60° = 12. 

Do đó: $\overrightarrow{AB}.\overrightarrow{AD}=12$. 

Ta cũng có: $\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AB}.\left(\overrightarrow{AB}+\overrightarrow{AD}\right)$

$={\overrightarrow{AB}}^2+\overrightarrow{AB}.\overrightarrow{AD}$ = AB² + 12 = 4² + 12 = 28. 

Do đó: $\overrightarrow{AB}.\overrightarrow{AC}=28$. 

Lại có: $\overrightarrow{BD}.\overrightarrow{AC}=\left(-\overrightarrow{AB}+\overrightarrow{AD}\right).\left(\overrightarrow{AB}+\overrightarrow{AD}\right)$

$=\left(\overrightarrow{AD}-\overrightarrow{AB}\right).\left(\overrightarrow{AD}+\overrightarrow{AB}\right)$

$={\overrightarrow{AD}}^2-{\overrightarrow{AB}}^2$

= AD² – AB² = 6² – 4² = 20. 

Vậy $\overrightarrow{BD}.\overrightarrow{AC}=20$

c) Áp dụng định lí côsin trong tam giác ABD có: 

BD² = AB² + AD² – 2 . AB . AD . cosA

        = 4² + 6² – 2 . 4 . 6 . cos 60° = 28

$\Rightarrow BD=\sqrt{28}=2\sqrt{7}$

Ta có:

$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$$\Rightarrow {\left(\overrightarrow{AC}\right)}^2={\left(\overrightarrow{AB}+\overrightarrow{AD}\right)}^2$

$\iff {\overrightarrow{AC}}^2={\overrightarrow{AB}}^2+2.\overrightarrow{AB}.\overrightarrow{AD}+{\overrightarrow{AD}}^2$

$\iff A{C}^2=A{B}^2+2\overrightarrow{AB}.\overrightarrow{AD}+A{D}^2$

Suy ra: AC² = 4² + 2 . 12 + 6² = 76

$\Rightarrow AC=\sqrt{76}=2\sqrt{19}$

Bài tập vận dụng:

Bài 1. Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của hai đường chéo AC và BD. Chứng minh rằng: $\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{CD}}$ = 2$\overrightarrow{\mathrm{MN}}$.

Hướng dẫn giải:

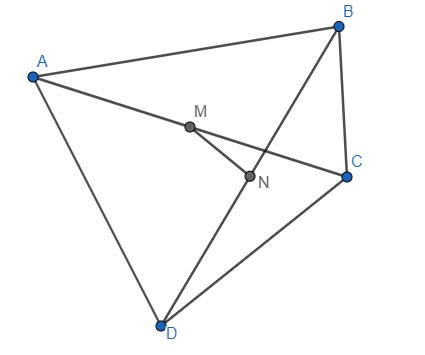
Ta có:

$\overrightarrow{\mathrm{MN}}$ = $\overrightarrow{\mathrm{MA}}$ + $\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{BN}}$

$\overrightarrow{\mathrm{MN}}$ = $\overrightarrow{\mathrm{MC}}$ + $\overrightarrow{\mathrm{CD}}$ + $\overrightarrow{\mathrm{DN}}$

Vì M, N lần lượt là trung điểm của hai đường chéo AC và BD

Suy ra:

$\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MC}}=\overrightarrow{0}$

$\overrightarrow{\mathrm{BN}}+\overrightarrow{\mathrm{DN}}=\overrightarrow{0}$

⇒ 2$\overrightarrow{\mathrm{MN}}$ = $\overrightarrow{\mathrm{MA}}$ + $\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{BN}}$ + $\overrightarrow{\mathrm{MC}}$ + $\overrightarrow{\mathrm{CD}}$ + $\overrightarrow{\mathrm{DN}}$

               = $\left(\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MC}}\right)$ + $\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{CD}}$ + $\left(\overrightarrow{\mathrm{BN}}+\overrightarrow{\mathrm{DN}}\right)$

               = $\overrightarrow{0}$ + $\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{CD}}$ + $\overrightarrow{0}$

               = $\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{CD}}$ (đpcm).

Bài 2. Một cây cột điện cao 20 m được đóng trên một triền dốc thẳng nghiêng hợp với phương nằm ngang một góc 17°. Người ta nối một dây cáp từ đỉnh cột điện đến cuối dốc. Tính chiều dài của dây cáp biết rằng đoạn đường từ đáy cọc đến cuối dốc bằng 72 m (làm tròn đến chữ số thập phân thứ 2).

Hướng dẫn giải:

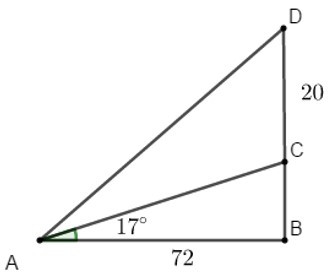
Bài toán được mô phỏng lại như hình vẽ với A, B lần lượt là điểm cuối dốc, chân của triền dốc; C, D lần lượt là chân và đỉnh của cây cột điện.

Suy ra chiều dài của dây cáp là đoạn AD.

Theo bài ra ta có: CD = 20 m, AB = 72 m, $\widehat{\mathrm{CAB}}$= 17°, $\widehat{\mathrm{ABD}}$= 90°.

$\widehat{\mathrm{ACB}}$= 180° – $\widehat{\mathrm{CAB}}$ – $\widehat{\mathrm{ABD}}$ = 180° – 17° – 90° = 73° (tổng ba góc một tam giác bằng 180°).

$\widehat{\mathrm{ACD}}$ = 180° – $\widehat{\mathrm{ACB}}$= 180° – 73° = 107°

Tam giác ABC vuông tại B ⇒ AC = $\frac{\mathrm{AB}}{\cos \widehat{\mathrm{CAB}}}$= $\frac{72}{\cos 17°}$≈ 75,3 (m)

Áp dụng định lí côsin trong tam giác ACD, ta có:

AD² = AC² + CD² – 2AC.CD.$\cos \widehat{\mathrm{ACD}}$

         = (75,3)² + 20² – 2.75,3.20.cos107° ≈ 6950,7

AD = 83,4m

Vậy chiều dài của dây cáp là 83,4m.

Bài 3. Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ $\overrightarrow{\mathrm{AN}}$, $\overrightarrow{\mathrm{MN}}$, $\overrightarrow{\mathrm{AG}}$ qua các vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{AC}}$.

Hướng dẫn giải:

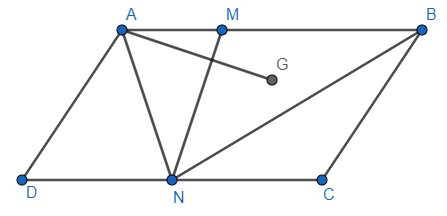
+ Vì ABCD là hình bình hành nên $\overrightarrow{\mathrm{BA}}$ = $\overrightarrow{\mathrm{CD}}$

Ta lại có: CD = 2CN nên N là trung điểm của CD.

Mà $\overrightarrow{\mathrm{CD}}$ và $\overrightarrow{\mathrm{CN}}$ là hai vectơ cùng hướng.

⇒ $\overrightarrow{\mathrm{CD}}=2\overrightarrow{\mathrm{CN}}$.

⇔ $\overrightarrow{\mathrm{CN}}=\frac{1}{2}\overrightarrow{\mathrm{CD}}$ ⟺ $\overrightarrow{\mathrm{CN}}=\frac{1}{2}\overrightarrow{\mathrm{BA}}$ ⟺ $\overrightarrow{\mathrm{CN}}=-\frac{1}{2}\overrightarrow{\mathrm{AB}}$

Suy ra:

$\overrightarrow{\mathrm{AN}}$ = $\overrightarrow{\mathrm{AC}}$ + $\overrightarrow{\mathrm{CN}}$ = $\overrightarrow{\mathrm{AC}}$ – $\frac{1}{2}\overrightarrow{\mathrm{AB}}$

+ Ta có: AB = 3AM ⇒ AM = $\frac{1}{3}$AB

Mà $\overrightarrow{\mathrm{AM}}$ và $\overrightarrow{\mathrm{AB}}$là hai vectơ cùng hướng.

⇒ $\overrightarrow{\mathrm{AM}}=\frac{1}{3}\overrightarrow{\mathrm{AB}}$  

⇒ $\overrightarrow{\mathrm{MA}}=-\frac{1}{3}\overrightarrow{\mathrm{AB}}$

⇒ $\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{AN}}$ = $-\frac{1}{3}\overrightarrow{\mathrm{AB}}$ + ($\overrightarrow{\mathrm{AC}}$ – $\frac{1}{2}\overrightarrow{\mathrm{AB}}$) = $-\frac{5}{6}\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}$ 

Vì G là trọng tâm tam giác MNB nên:

$3\overrightarrow{\mathrm{AG}}=\overrightarrow{\mathrm{AM}}+\overrightarrow{\mathrm{AN}}+\overrightarrow{\mathrm{AB}}$ = $\frac{1}{3}\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{AC}}$ – $\frac{1}{2}\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{AB}}$= $\frac{5}{6}\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}$

⇒ $\overrightarrow{\mathrm{AG}}=\frac{5}{18}\overrightarrow{\mathrm{AB}}+\frac{1}{3}\overrightarrow{\mathrm{AC}}$

Vậy:

$\overrightarrow{\mathrm{AN}}$ = $\overrightarrow{\mathrm{AC}}$ – $\frac{1}{2}\overrightarrow{\mathrm{AB}}$

$\overrightarrow{\mathrm{MN}}$ = $-\frac{5}{6}\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}$

$\overrightarrow{\mathrm{AG}}=\frac{5}{18}\overrightarrow{\mathrm{AB}}+\frac{1}{3}\overrightarrow{\mathrm{AC}}$