Với giải Bài 1 trang 59 Toán lớp 7 Cánh diều chi tiết trong Bài 3: Phép cộng, phép trừ đa thức một biến giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 3: Phép cộng, phép trừ đa thức một biến

Bài 1 trang 59 Toán 7 Tập 2: Cho hai đa thức: R(x) = -8x4 + 6x3 + 2x2 - 5x + 1 và S(x) = x4 - 8x3 + 2x + 3. Tính:

a) R(x) + S(x);

b) R(x) - S(x).

Lời giải:

a) Cách 1: Tính tổng R(x) + S(x) theo cột dọc:

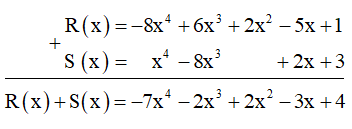
Vậy R(x) + S(x) = -7x4 - 2x3 + 2x2 - 3x + 4.

Cách 2: Tính tổng R(x) + S(x) theo hàng ngang:

R(x) + S(x)

= (-8x4 + 6x3 + 2x2 - 5x + 1) + (x4 - 8x3 + 2x + 3)

= -8x4 + 6x3 + 2x2 - 5x + 1 + x4 - 8x3 + 2x + 3

= (-8x4 + x4) + (6x3 - 8x3) + 2x2 + (-5x + 2x) + (1 + 3)

= -7x4 - 2x3 + 2x2 - 3x + 4.

Vậy R(x) + S(x) = -7x4 - 2x3 + 2x2 - 3x + 4.

b) Cách 1: Tính hiệu R(x) ‒ S(x) theo cột dọc:

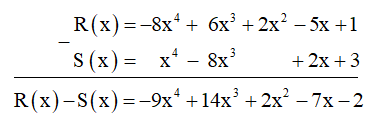
Vậy R(x) - S(x) = -9x4 + 14x3 + 2x2 - 7x - 2.

Cách 2: Tính hiệu R(x) ‒ S(x) theo hàng ngang:

R(x) - S(x) = (-8x4 + 6x3 + 2x2 - 5x + 1) - (x4 - 8x3 + 2x + 3)

= -8x4 + 6x3 + 2x2 - 5x + 1 - x4 + 8x3 - 2x - 3

= (-8x4 - x4) + (6x3 + 8x3) + 2x2 + (-5x - 2x) + (1 - 3)

= -9x4 + 14x3 + 2x2 - 7x - 2

Vậy R(x) - S(x) = -9x4 + 14x3 + 2x2 - 7x - 2.