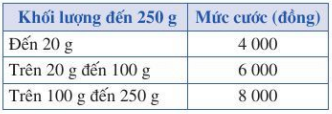
a) Số tiền dịch vụ thư cơ bản phải trả y (đồng) có là hàm số của khối lượng thư cơ bản x(g) hay không? Nếu đúng, hãy xác định những công thức tính y.

b) Tính số tiền phải trả khi bạn Dương gửi thư có khối lượng 150g, 200g.

Lời giải:

a) Ta thấy với mỗi giá trị của x có đúng 1 giá trị của y tương ứng nên y là hàm số của x.

Công thức tính y:

$y=\{\begin{array}{l}2000\mathrm{k}\mathrm{h}\mathrm{i}x\le 20\\ 6000\mathrm{k}\mathrm{h}\mathrm{i}20<x\le 100\\ 8000\mathrm{k}\mathrm{h}\mathrm{i}100<x\le 250\end{array}$

b) Với x=150 thì y=8000

Với x=200 thì y=8000

Bài tập vận dụng:

Bài 1. Cho đồ thị hàm số y = f(x) như hình.

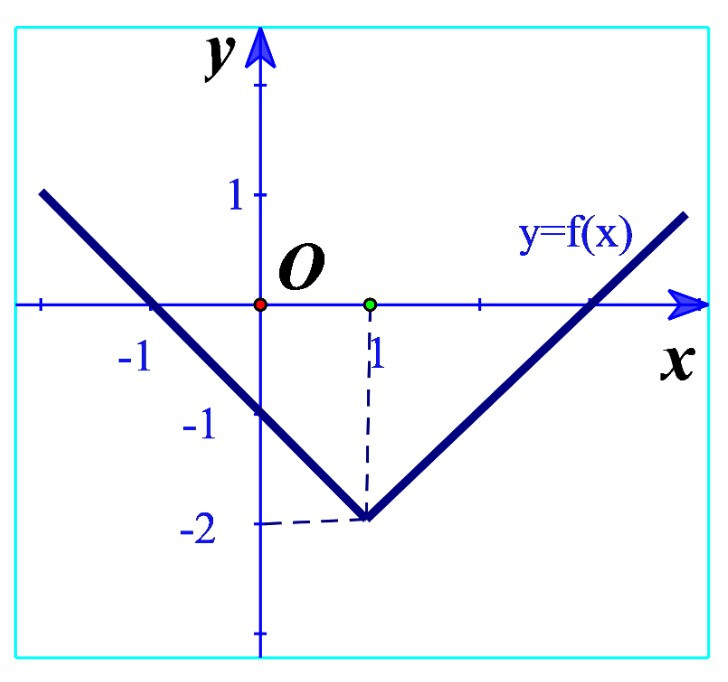
a) Trong các điểm có toạ độ (1; –2); (0; 0); (2; –1) điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?

b) Xác định f(0); f(3).

c) Tìm điểm thuộc đồ thị có tung độ bằng 0.

Hướng dẫn giải

a) Ta xác định các điểm A, O, B tương ứng với tọa độ (1; –2); (0; 0); (2; –1) trên hình:

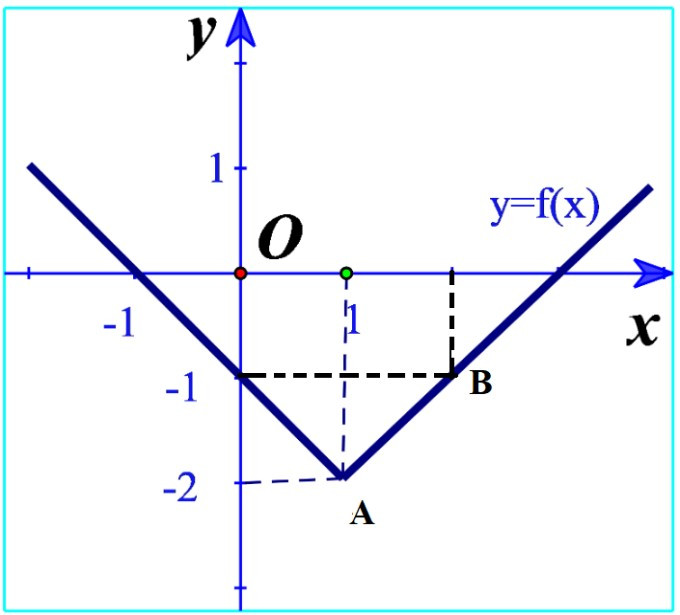
Quan sát đồ thị ta thấy điểm A có hoành độ bằng 1 và tung độ bằng –2 thuộc đồ thị của hàm số; Điểm B có hoành độ bằng 2 và tung độ bằng –1 thuộc đồ thị của hàm số; Điểm (0; 0) không thuộc đồ thị hàm số.

b)

– Giá trị của f(0) chính là giao điểm của đường thẳng x = 0 với đồ thị hàm số y = f(x). Quan sát đồ thị ta thấy giao điểm có hoành độ bằng –1 nên f(0) = –1

– Giá trị của f(3) chính là giao điểm của đường thẳng x = 3 với đồ thị hàm số y = f(x). Quan sát đồ thị ta thấy đường thẳng x = 3 song song với Oy nên f(3) = 0

Vậy f(0) = –1 và f(3) = 0.

c) Điểm thuộc đồ thị có tung độ bằng 0 chính là giao điểm của đường thẳng y = 0 và đồ thị. Quan sát đồ thị ta thấy có hai giao điểm với hoành độ là x = – 1 và x = 3.

Do đó ta có hai giao điểm của đồ thị  và trục Ox là (–1; 0) và (3; 0).

Bài 2. Cho hàm số y = –2.x²

a) Điểm nào trong các điểm (−1; −2); (0; 0); (0; 1); (2021; 1) thuộc đồ thị của hàm số trên?

b) Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng −2; 3 và 10.

c) Tìm những điểm thuộc đồ thị hàm số có tung độ bằng −18.

Hướng dẫn giải

a)

– Thay toạ độ (–1; –2) vào hàm số y = –2.x² ta được: –2 = –2. (– 1)²  (Đúng). Như vậy, điểm (–1; –2) thuộc đồ thị.

– Thay toạ độ (0; 0) vào hàm số y = –2.x² ta được: 0 = –2.0² (Đúng). Như vậy điểm (0; 0) thuộc đồ thị.

– Thay toạ độ (0;1) vào hàm số y = –2.x² ta được: 1 = –2.0² = 0 (Sai). Như vậy điểm (0; 1) không thuộc đồ thị.

– Thay điểm toạ độ  (2021; 1) vào hàm số y = –2.x² ta được: 1 = –2.2021² (Sai). Như vậy điểm (2021; 1) không thuộc đồ thị.

b)

– Thay x = –2 vào hàm số y = –2.x², ta được: y = –2.(– 2)² = –8. Khi đó ta được điểm có tọa độ (–2; –8).

– Thay x = 3 vào hàm số y = –2.x², ta được: y = –2.3² = –18. Khi đó ta được điểm có tọa độ (3; –18).

– Thay x = 10 vào hàm số y = –2.x², ta được: y = –2.10² = –200. Khi đó ta được điểm có tọa độ (10; –200).

Vậy những điểm cần tìm là: (–2; –8); (3; –18) và (10; –200).

c) Thay y = –18 vào hàm số y = –2.x², ta được: –18 = –2.x² ⇔ x² = 9 ⇔ x = ±3. Khi đó ta được hai điểm có tọa độ (3; –18) và (–3; –18).

Vậy tọa độ những điểm cần tìm là (3; –18) và (–3; –18).

Bài 3. Tìm tập xác định của mỗi hàm số sau:

a) y = – x²;  

b) y = $\sqrt{2-3\mathrm{x}}$;     

c) y = $\frac{4}{\mathrm{x}+1}$;

d) y= $\left\{\begin{array}{l}1\text{ khi }\mathrm{x}\in \mathrm{\mathbb{Q}}\\ 0\text{ khi }\mathrm{x}\in \mathrm{ℝ}\backslash \mathrm{\mathbb{Q}}\end{array}\right.$.

Hướng dẫn giải

a) Tập xác định  D = ℝ.

b) Biểu thức $\sqrt{2-3\mathrm{x}}$ có nghĩa khi 2 – 3x ≥ 0 ⇔ x ≤ $\frac{2}{3}$. Vì vậy tập xác định của hàm số: $\mathrm{D}\text{ = }\left\{\mathrm{x}\in \mathrm{ℝ}\text{| }\mathrm{x}\le \frac{2}{3}\right\}\text{= }\left(-\infty ;\frac{2}{3}\right]$.

c) Biểu thức y = $\frac{4}{\mathrm{x}+1}$ có nghĩa khi x + 1 ≠ 0 ⇔ x ≠ – 1. Vì vậy tập xác định của hàm số: $\mathrm{D}\text{ = }\left\{\mathrm{x}\in \mathrm{ℝ}\text{| }\mathrm{x}\ne -1\right\}\text{= }\mathrm{ℝ}\text{}\left\{-1\right\}$.

d) Ta thấy hàm số có nghĩa với mọi x ∈ ℚ và x ∈ ℝ \ ℚ nên tập xác định của hàm số là: D = ℝ.