Với giải Hoạt động 6 trang 36 Toán lớp 10 Cánh diều chi tiết trong Bài 1: Hàm số và đồ thị giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 1: Hàm số và đồ thị

Hoạt động 6 trang 36 Toán lớp 10: Cho đồ thị hàm số $y=f\left(x\right)=x^2$ như Hình 6.

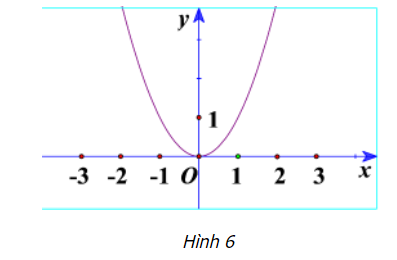
a) So sánh $f\left(-2\right),f\left(-1\right)$. Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ -2 đến -1.

b) So sánh $f\left(1\right),f\left(2\right)$. Nêu nhận xét về sự biến thiên của giá trị hàm số khị giá trị biến x tăng dần từ 1 đến 2.

Phương pháp giải:

a)

- Tính $f\left(-2\right),f\left(-1\right)$

- Lấy $x_1,x_2\in \left(-2;-1\right)$ sao cho $x_1<x_2$. Chứng minh $f\left(x_1\right)>f\left(x_2\right)$

b)

- Tính $f\left(1\right),f\left(2\right)$

- Lấy $x_1,x_2\in \left(1;2\right)$ sao cho $x_1<x_2$. Chứng minh $f\left(x_1\right)>f\left(x_2\right)$

Lời giải:

a) $f\left(-2\right)={\left(-2\right)}^2=4;$$f\left(-1\right)={\left(-1\right)}^2=1$

$\Rightarrow f\left(-2\right)>f\left(-1\right)$

Lấy $x_1,x_2\in \left(-2;-1\right)$ sao cho $x_1<x_2$.

$\Rightarrow x_1-x_2<0$

$x_1,x_2<0\Rightarrow x_1+x_2<0$

Ta có:

$\begin{array}{l}f\left(x_1\right)=x_1^2;f\left(x_2\right)=x_2^2\\ f\left(x_1\right)-f\left(x_2\right)=x_1^2-x_2^2\\ =\left(x_1-x_2\right).\left(x_1+x_2\right)>0\\ \Rightarrow f\left(x_1\right)>f\left(x_2\right)\end{array}$

=> Hàm số nghịch biến trên (-2;-1)

Vậy hàm số giảm khi x tăng từ -2 đến -1

b) $\begin{array}{l}f\left(1\right)=1;f\left(2\right)=2^2=4\\ \Rightarrow f\left(1\right)<f\left(2\right)\end{array}$

Lấy $x_1,x_2\in \left(1;2\right)$ sao cho $x_1<x_2$.

$\Rightarrow x_1-x_2<0$

$x_1,x_2>0\Rightarrow x_1+x_2>0$

Ta có:

$\begin{array}{l}f\left(x_1\right)=x_1^2;f\left(x_2\right)=x_2^2\\ f\left(x_1\right)-f\left(x_2\right)=x_1^2-x_2^2\\ =\left(x_1-x_2\right).\left(x_1+x_2\right)<0\\ \Rightarrow f\left(x_1\right)<f\left(x_2\right)\end{array}$

=> Hàm số đồng biến trên (1;2)

Vậy hàm số tăng khi x tăng từ 1 đến 2.

Lý thuyết Sự biến của hàm số

Cho hàm số y = f(x) xác định trên khoảng (a; b):

- Hàm số y = f(x) gọi là đồng biến trên khoảng (a; b) nếu

$\forall x_1,x_2\in \left(a;b\right),x_1<x_2\Rightarrow f\left(x_1\right)<f\left(x_2\right)$

- Hàm số y = f(x) gọi là nghịch biến trên khoảng (a; b) nếu

$\forall x_1,x_2\in \left(a;b\right),x_1<x_2\Rightarrow f\left(x_1\right)>f\left(x_2\right)$

Ví dụ: Cho hàm số y = f(x) = $x^2$

Xét sự biến thiên của hàm số trên khoảng (-∞; 0) và (0; +∞).

Hướng dẫn giải

+) Trên khoảng (-∞; 0) hàm số luôn xác định

Lấy x₁, x₂ ∈ (-∞; 0) thỏa mãn x₁ < x₂.

Vì x₁ < x₂ < 0 nên x₁² > x₂² hay f(x₁) > f(x₂)

Do đó hàm số nghịch biến trên (-∞; 0).

+) Trên khoảng (0; +∞) hàm số luôn xác định

Lấy x₁, x₂ ∈ (0; +∞) thỏa mãn x₁ < x₂.

Vì 0 < x₁ < x₂ nên x₁² < x₂² hay f(x₁) < f(x₂)

Do đó hàm số đồng biến trên (0; +∞).

Vậy hàm số đã cho nghịch biến trên (-∞; 0) và đồng biến trên (0; +∞).

Bảng biến thiên:

Đây là bảng thiên của hàm số y = x².

- Dấu mũi tên đi xuống từ +∞ đến 0 diễn tả hàm số nghịch biến trên khoảng (-∞; 0)

- Dấu mũi tên đi lên từ 0 đến +∞ diễn ta hàm số đồng biến trên khoảng (0; +∞).

Đồ thị hàm số:

- Ta thấy hàm số nghịch biến trên khoảng (-∞; 0) khi đồ thị hàm số trên khoảng đó “đi xuống”.

- Hàm số đồng biến trên khoảng (0; +∞) khi đồ thị hàm số trên khoảng đó “đi lên”.

Xem thêm các bài giải Toán lớp 10 Cánh diều hay, chi tiết khác:

Câu hỏi khởi động trang 31 Toán lớp 10: Làm thế nào để mô tả được mối liên hệ giữa thời gian t và quãng đuờmg đi đuợc S của vật rơi tự do?...

Hoạt động 1 trang 31 Toán lớp 10: Trong bài toán ở phần mở đầu, ta đã biết công thức tính quãng đường...

Hoạt động 2 trang 31 Toán lớp 10: Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệp tính toán lợi nhuận y (đồng) theo công thức...

Luyện tập vận dụng 1 trang 32 Toán lớp 10: Trong y học, một người cân nặng 60 kg chạy với tốc độ 6,5 km/h thì lượng ca-lo tiêu thụ...

Hoạt động 3 trang 32 Toán lớp 10: Cho hai hàm số...

Luyện tập vận dụng 2 trang 32 Toán lớp 10: Tìm tập xác định...

Luyện tập vận dụng 3 trang 33 Toán lớp 10: Cho hàm số:...

Hoạt động 4 trang 34 Toán lớp 10: Xét hàm số...

Luyện tập vận dụng 4 trang 34 Toán lớp 10: Cho hàm số...

Luyện tập vận dụng 5 trang 35 Toán lớp 10: Dựa vào Hình 4,...

Hoạt động 5 trang 36 Toán lớp 10: Cho hàm số...

Luyện tập vận dụng 6 trang 36 Toán lớp 10: Chứng tỏ hàm số...

Bài 1 trang 37 Toán lớp 10: Tìm tập xác định của mỗi hàm số sau:....

Bài 2 trang 37 Toán lớp 10: Bảng 1 dưới đây cho biết chỉ số...

Bài 3 trang 38 Toán lớp 10: Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ...

Bài 4 trang 37 Toán lớp 10: Cho hàm số ...

Bài 5 trang 37 Toán lớp 10:  Cho đồ thị hàm số....

Bài 6 trang 37 Toán lớp 10: Cho hàm số...

Bài 7 trang 37 Toán lớp 10:  Cho hàm số...

Bài 8 trang 37 Toán lớp 10: Một lớp muốn thuê một chiếc xe khách cho chuyến tham quan với tổng đoạn đường cần di chuyển trong khoảng từ 550 km đến 600 km, có hai công ty được tiếp cận để tham khảo giá....

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc hai một ẩn