Với giải Bài 6 trang 76 SBT Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 4: Ba đường conic trong mặt phẳng tọa độ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải sách bài tập Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài 6 trang 76 SBT Toán 10 Tập 2: Một cái cầu có dây cáp treo hình parabol, cầu dài 120 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 48 m, thanh ngắn nhất là 8 m (Hình 12). Tính chiều dài của thanh cách điểm giữa cầu 20 m.
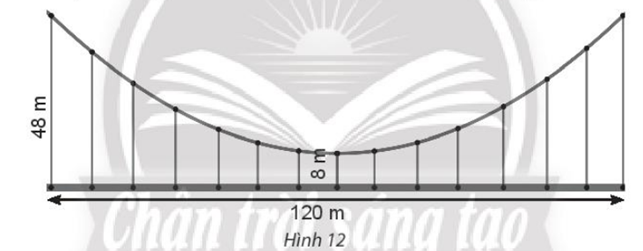
Lời giải:
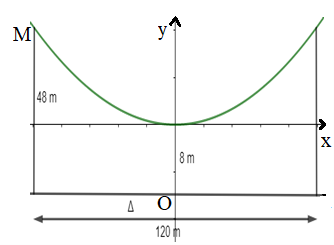
Ta chọn hệ quy chiếu như hình vẽ
Parabol có phương trình y2 = 2px (p > 0)
Thay toạ độ điểm M(40; 60) vào phương trình ta được
602 = 2.p.40 p = 45
Vậy phương trình chính tắc của Parabol là: y2 = 90x
Vì thanh cách điểm giữa cầu là 20 m nên ta có điểm N(x; 20) thuộc Parabol nên ta có: 202 = 90.x
Vậy thanh có độ dài 8 + 4,4 = 12,4 m.
Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 75 SBT Toán 10 Tập 2: Viết phương trình chính tắc của:...
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Đường tròn trong mặt phẳng tọa độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài 1: Không gian mẫu và biến cố
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
