Với giải sách bài tập Toán 10 Bài 4: Ba đường conic trong mặt phẳng tọa độ sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng tọa độ

Giải SBT Toán 10 trang 75 Tập 2

Bài 1 trang 75 SBT Toán 10 Tập 2: Viết phương trình chính tắc của:

a) Elip có trục lớn bằng 12 và trục nhỏ bằng 8;

b) Hypebol có tiêu cự 2c = 18 và độ dài trục thực 2a = 14;

c) Parabol có tiêu điểm F(5; 0).

Lời giải:

a) Ta có:

Trục lớn 2a = 12 ⇒ a = 6;

Trục bé 2b = 8 ⇒ b = 4.

Vậy phương trình chính tắc của Elip là:  $\frac{x^2}{36}+\frac{y^2}{16}=1$

b) Ta có:

Tiêu cự 2c = 18 ⇒ c = 9

Trục thực 2a = 14 ⇒ a = 7

Mặt khác, ta có: b² = c² – a² = 9² – 7² = 32.

Vậy phương trình chính tắc của Hypebol là: $\frac{x^2}{49}-\frac{y^2}{32}=1$ .

c) Parabol có tiêu điểm F(5; 0) nên ta có $\frac{p}{2}=5$  suy ra p = 10.

Vậy Parabol có phương trình y² = 20x.

Bài 2 trang 75 SBT Toán 10 Tập 2: Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm toạ độ các tiêu điểm của chúng.

a) $\left(C_1\right):7x^2+13y^2=1$ ;

b) $\left(C_2\right):25x^2-9y^2=225$ ;

c) $\left(C_3\right):x=2y^2$ .

Lời giải:

a) $\left(C_1\right):7x^2+13y^2=1$

 $\iff \frac{x^2}{\frac{1}{7}}+\frac{y^2}{\frac{1}{13}}=1$

Đây là phương trình chính tắc của Elip

Ta có  $a=\frac{\sqrt{7}}{7};b=\frac{\sqrt{13}}{13}$ và c =  $\sqrt{a^2-b^2}=\sqrt{\frac{1}{7}-\frac{1}{13}}=\frac{\sqrt{546}}{91}$

Các tiêu điểm  $F_1\left(-\frac{\sqrt{546}}{91};0\right);F_2\left(\frac{\sqrt{546}}{91};0\right)$

b) (C₂): 25x² – 9y² = 225

 $\iff \frac{x^2}{9}-\frac{y^2}{25}=1$

 $\iff \frac{x^2}{3^2}-\frac{y^2}{5^2}=1$

Đây là phương trình chính tắc của Hypebol

Ta có a = 3; b = 5 và c² = a² + b² = 3² + 5² = 34.

Các tiêu điểm $F_1=\left(-\sqrt{34};0\right),F_2\left(\sqrt{34};0\right)$ .

c) (C₃): x = 2y²

$\iff$ y² = $\frac{1}{2}$ x

Đây là phương trình chính tắc của Parabol

Ta có 2p = $\frac{1}{2}$  suy ra p =  $\frac{1}{4}$

Tiêu điểm $F\left(\frac{1}{8};0\right)$.

Bài 3 trang 75 SBT Toán 10 Tập 2:  Để cắt một bảng hiệu quảng cáo hình elip có trục lớn là 1 m và trục nhỏ là 0,6 m từ một tấm ván ép hình chữ nhật có kích thước 1 m x 0,6 m, người ta vẽ hình elip đó lên tấm ván ép như hướng dẫn sau:

Chuẩn bị:

- Hai cái đinh, một vòng dây kín không đàn hồi, bút chì.

Thực hiện:

- Xác định vị trí (hai tiêu điểm của elip) và ghim hai cái đinh lên hai điểm đó trên tâm ván.

- Quàng vòng dây qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chỉ vạch lên tấm bìa một đường mà ta gọi là đường elip. (Xem minh hoạ trong Hình 10).

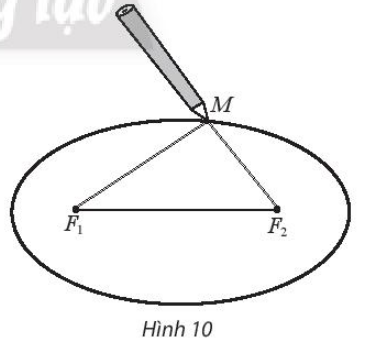
Phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu và lấy vòng dây có độ dài là bao nhiêu?

Lời giải:

Ta có:

Trục lớn 2a = 1 ⇒ a = 0,5

Trục bé 2b = 0,6 ⇒ b = 0,3

Khi đó: c² = a² – b² = 0,5² – 0,3² = 0,16

$\Rightarrow$ c = 0,4 m = 40 cm

Các tiêu điểm F₁(- 40, 0), F₂(40; 0)

Độ dài vòng dây là: MF₁ + MF₂ + F₁F₂ = 2a + 2c = 2.0,5 + 2. 0,4 = 1,8 m.

Vậy hai cái đinh để cách mép phải và mép trái của tấm ván ép 10 cm. Lấy vòng dây có độ dài 1,8 m = 180 cm.

Giải SBT Toán 10 trang 76 Tập 2

Bài 4 trang 76 SBT Toán 10 Tập 2: Thang leo gợn sóng cho trẻ em trong công viên có hai khung thép cong hình nửa elip cao 100 cm và khoảng cách giữa hai chân là 240 cm.

a) Hãy chọn hệ toạ độ thích hợp và viết phương trình chính tắc của elip nói trên.

b) Tính khoảng cách thẳng đứng từ một điểm cách chân khung 20 cm lên đến khung thép.

Lời giải:

a) Ta có a = 120; b = 100

Vậy phương trình chính tắc của Elip là:  $\frac{x^2}{14400}+\frac{y^2}{10000}=1$

b)

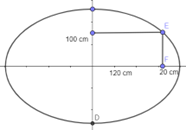
Giả sử thang có hình Elip như hình vẽ

Gọi F là điểm cách chân khung 20 cm.

⇒ OF = 120 – 20 = 100 cm

Suy ra độ dài đoạn FE là khoảng cách cần tìm

Vậy toạ độ của E(100; y); (y > 0)

Vì E thuộc Elip nên ta có $\frac{{100}^2}{14400}+\frac{y^2}{10000}=1$ $\iff$ y² =

 $\Rightarrow y=\frac{50\sqrt{11}}{3}$

Vậy  $E\left(100;\frac{50\sqrt{11}}{3}\right)$

Ta có khoảng cách thẳng đứng từ điểm cách chân khung 20 cm đến khung thép là  $\frac{50\sqrt{11}}{3}\approx$ 55 cm.

Bài 5 trang 76 SBT Toán 10 Tập 2: Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol có phương trình $\frac{x^2}{{30}^2}-\frac{y^2}{{50}^2}=1$ . Biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng $\frac{1}{2}$  khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.

Lời giải:

Gọi bán kính nóc tháp là r, đáy tháp là R

Vì khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng $\frac{1}{2}$  khoảng cách từ tâm đối xứng đến đáy nên ta có khoảng cách từ nóc tháp đến tâm đối là 40 m, khoảng cách từ tâm đối xứng đến đáy là 80 m.

Do điểm M(r, 40) và điểm N(R; - 80) thuộc hypebol nên ta có

$\frac{r^2}{{30}^2}-\frac{{40}^2}{{50}^2}=1\Rightarrow r=30\sqrt{1+\frac{{40}^2}{{50}^2}}=6\sqrt{41}$ $\approx$38 m

$\frac{R^2}{{30}^2}-\frac{{(-80)}^2}{{50}^2}=1\Rightarrow R=30\sqrt{1+\frac{{(-80)}^2}{{50}^2}}=6\sqrt{89}\approx 57$ m

Vậy bán kính nóc tháp là 38 m; bán kính đáy tháp là 57 m.

Bài 6 trang 76 SBT Toán 10 Tập 2: Một cái cầu có dây cáp treo hình parabol, cầu dài 120 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 48 m, thanh ngắn nhất là 8 m (Hình 12). Tính chiều dài của thanh cách điểm giữa cầu 20 m.

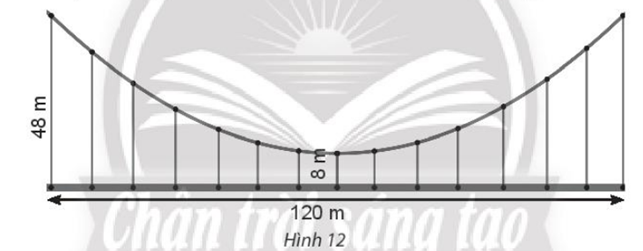
Lời giải:

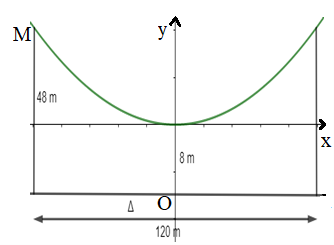
Ta chọn hệ quy chiếu như hình vẽ

Parabol có phương trình y² = 2px (p > 0)

Thay toạ độ điểm M(40; 60) vào phương trình ta được

60² = 2.p.40 $\Rightarrow$  p = 45

Vậy phương trình chính tắc của Parabol là: y² = 90x

Vì thanh cách điểm giữa cầu là 20 m nên ta có điểm N(x; 20) thuộc Parabol nên ta có: 20² = 90.x$\Rightarrow x=\mathrm{4,4}$

Vậy thanh có độ dài 8 + 4,4 = 12,4 m.

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Đường tròn trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố

Lý thuyết Ba đường conic trong mặt phẳng tọa độ

1. Elip

1.1. Nhận biết elip

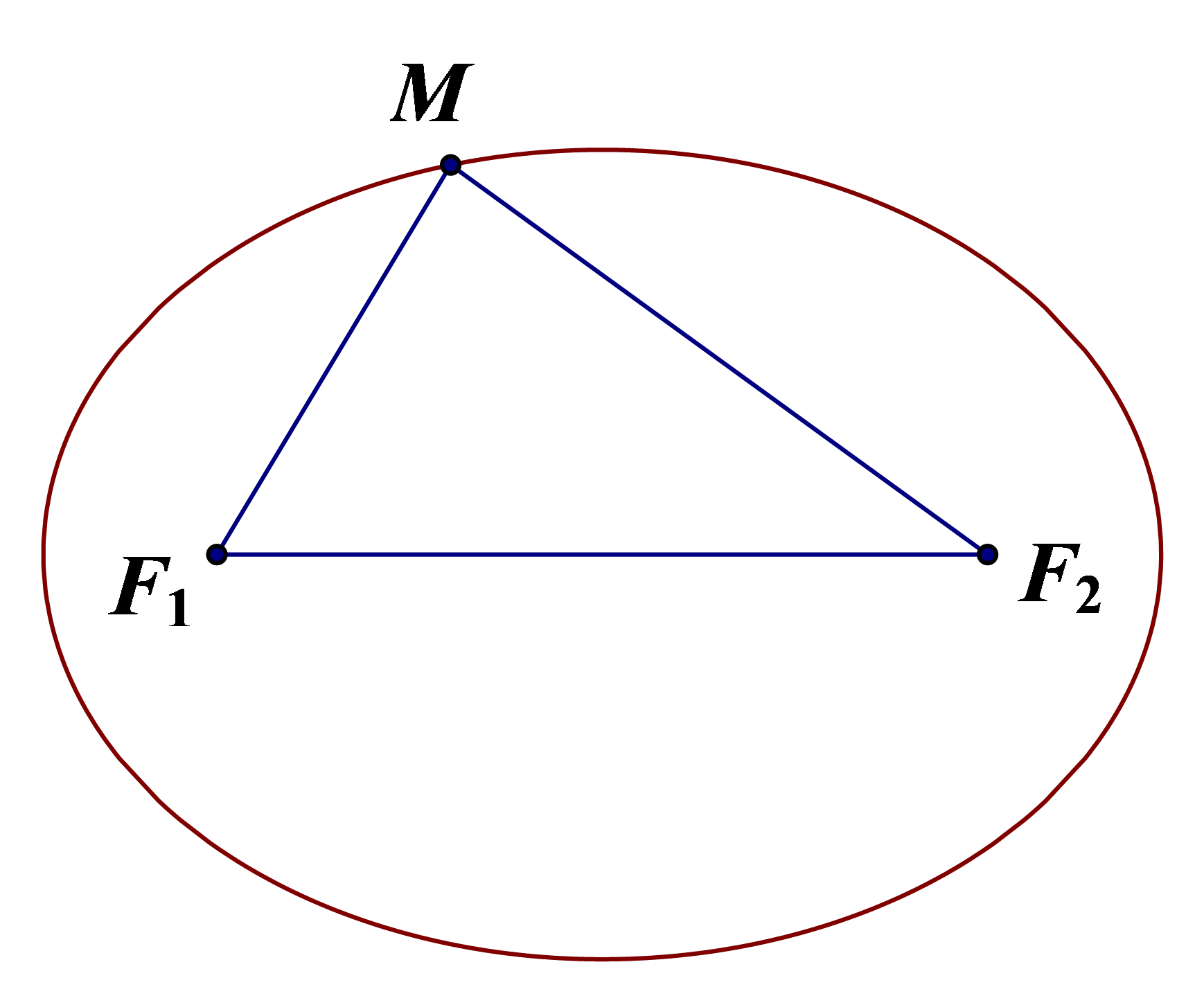
Cho hai điểm cố định F₁, F₂ và một độ dài không đổi 2a lớn hơn F₁F₂. Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho F₁M + F₂M = 2a.

Các điểm F₁ và F₂ gọi là các tiêu điểm của elip.

Độ dài F₁F₂ = 2c gọi là tiêu cự của elip (a > c).

1.2. Phương trình chính tắc của elip

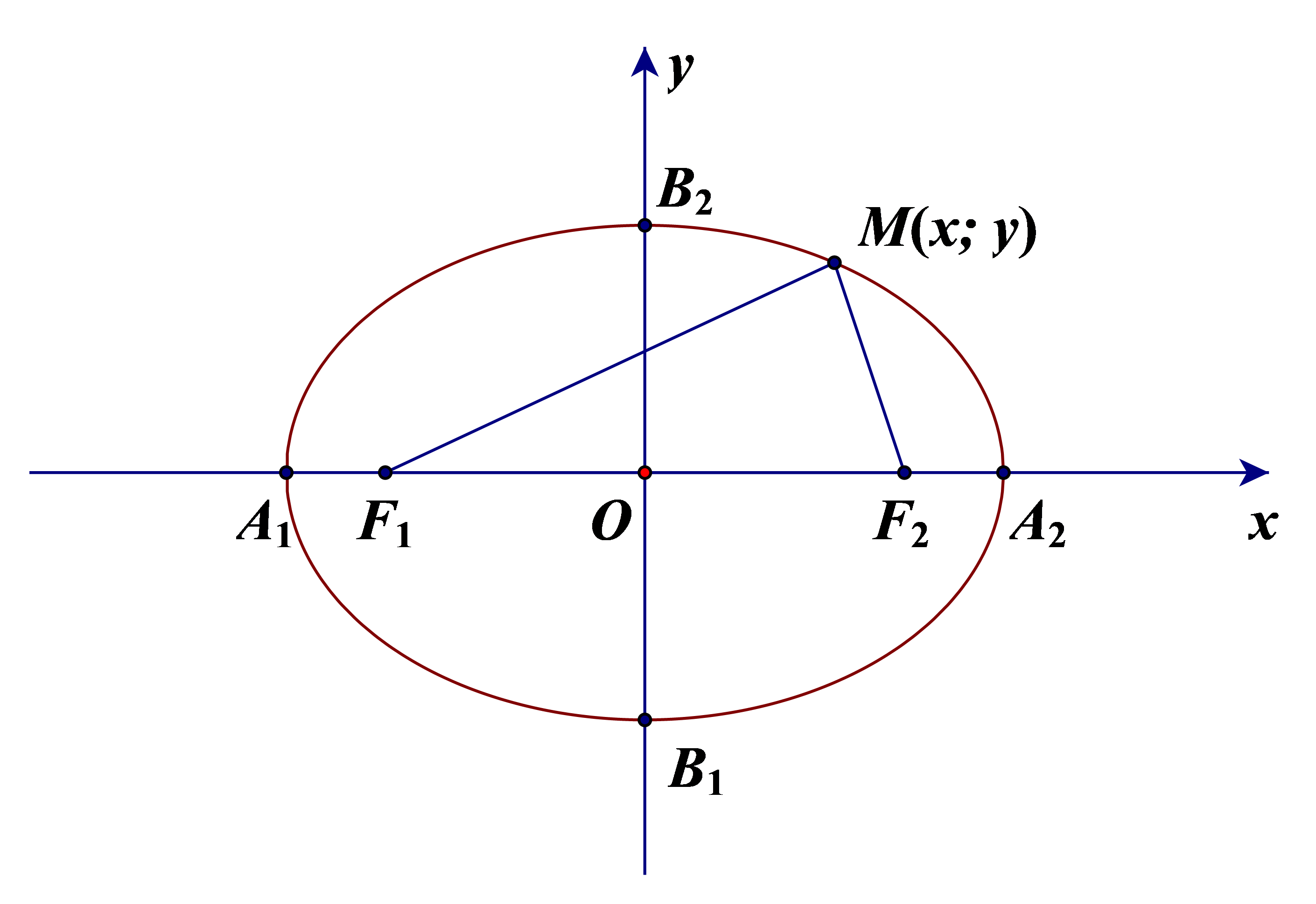
Cho elip (E) có các tiêu điểm F₁ và F₂ và đặt F₁F₂ = 2c. Chọn hệ trục tọa độ Oxy sao cho F₁(–c; 0) và F₂(c; 0).

Người ta chứng minh được:

$M\left(x;y\right)\in \left(E\right)\iff \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$   (1),

trong đó $b=\sqrt{a^2-c^2}$.

Phương trình (1) gọi là phương trình chính tắc của elip.

Chú ý:

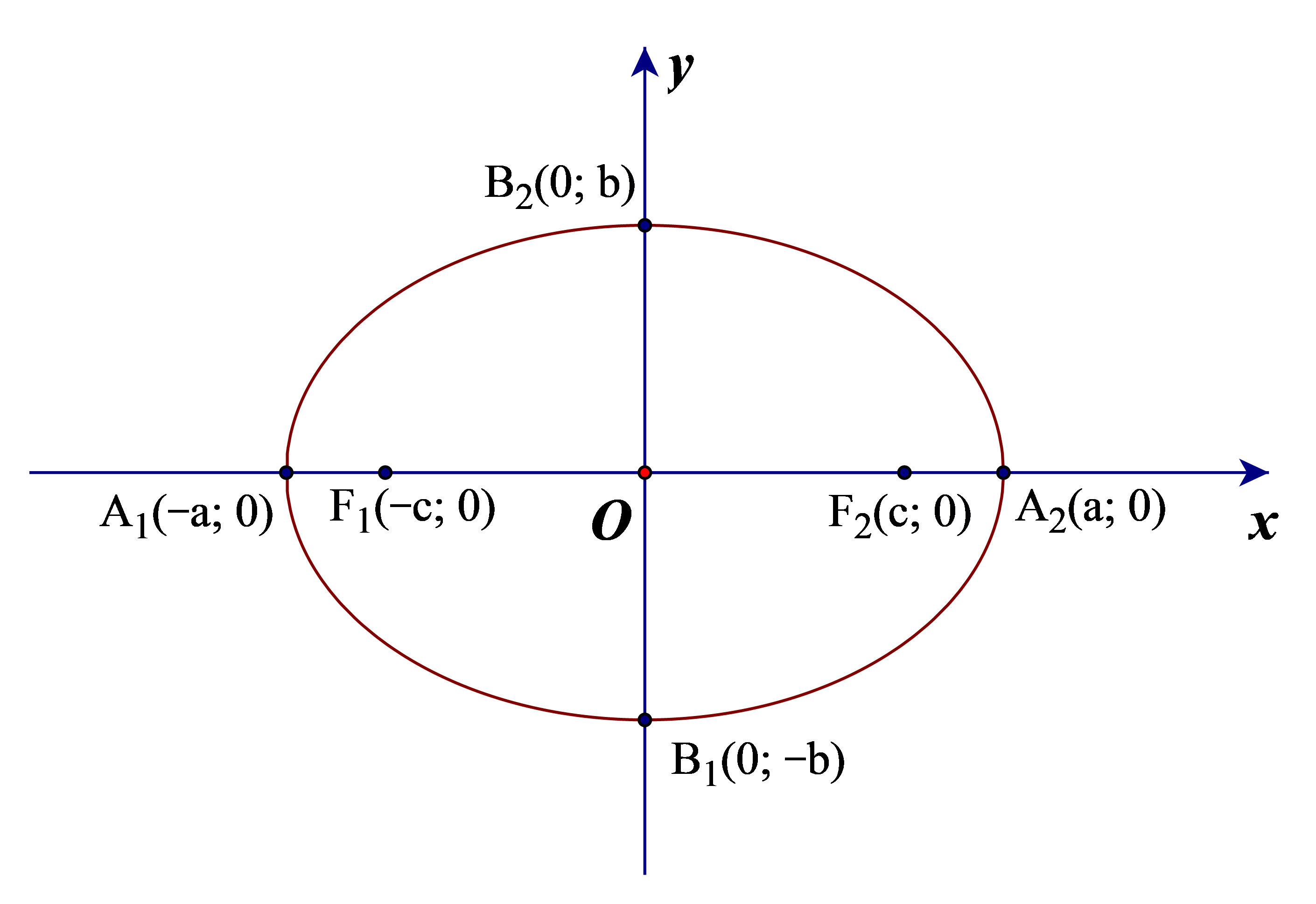
• (E) cắt Ox tại hai điểm A₁(–a; 0), A₂(a; 0) và cắt Oy tại hai điểm B₁(0; –b), B₂(0; b).

• Các điểm A₁, A₂, B₁, B₂ gọi là các đỉnh của elip.

• Đoạn thẳng A₁A₂ = 2a gọi là trục lớn, đoạn thẳng B₁B₂ = 2b gọi là trục nhỏ của elip.

• Giao điểm O của hai trục gọi là tâm đối xứng của elip.

• Nếu M(x; y) ∈ (E) thì |x| ≤ a, |y| ≥ b.

Ví dụ: Cho elip (E) có độ dài trục lớn bằng 10, tỉ số giữa tiêu cự và độ dài trục lớn là $\frac{2}{5}$.

a) Tính độ dài trục nhỏ của elip.

b) Viết phương trình chính tắc của elip.

Hướng dẫn giải

a) Ta có độ dài trục lớn bằng 10. Ta suy ra 2a = 10.

Suy ra a = 5.

Theo đề, ta có tỉ số giữa tiêu cự và độ dài trục lớn là $\frac{2}{5}$.

Suy ra $\frac{2c}{2a}=\frac{2}{5}$.

$\iff c=\frac{2}{5}.a=\frac{2}{5}.10=4$.

Ta có $b=\sqrt{a^2-c^2}=\sqrt{5^2-4^2}=3$.

Suy ra 2b = 2.3 = 6.

Vậy độ dài trục nhỏ của elip (E) bằng 6.

b) Ta có a = 5 và b = 3.

Phương trình chính tắc của elip (E) là: $\frac{x^2}{25}+\frac{y^2}{9}=1$.

2. Hypebol

2.1. Nhận biết hypebol

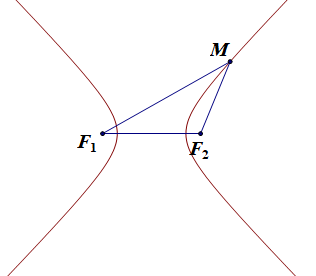
Cho hai điểm cố định F₁, F₂ và một độ dài không đổi 2a nhỏ hơn F₁F₂. Hypebol (H) là tập hợp các điểm M trong mặt phẳng sao cho |F₁M – F₂M| = 2a.

Các điểm F₁ và F₂ gọi là các tiêu điểm của hypebol.

Độ dài F₁F₂ = 2c gọi là tiêu cự của hypebol (c > a).

2.2. Phương trình chính tắc của hypebol

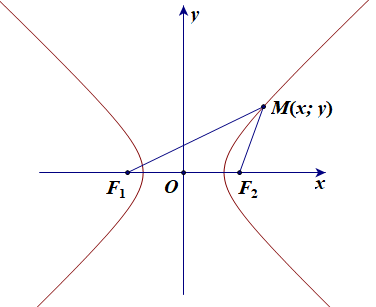
Cho hypebol (H) có các tiêu điểm F₁ và F₂ và đặt F₁F₂ = 2c. Điểm M thuộc hypebol (H) khi và chỉ khi |F₁M – F₂M| = 2a. Chọn hệ trục tọa độ Oxy sao cho F₁(–c; 0) và F₂(c; 0).

Người ta chứng minh được:

$M\left(x;y\right)\in \left(H\right)\iff \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$   (2),

trong đó $b=\sqrt{c^2-a^2}$.

Phương trình (2) gọi là phương trình chính tắc của hypebol.

Chú ý:

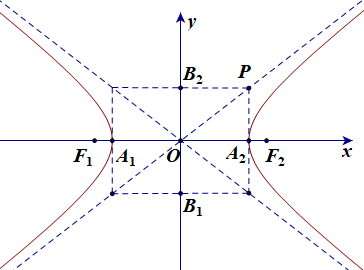
• (H) cắt Ox tại hai điểm A₁(–a; 0) và A₂(a; 0). Nếu ta vẽ hai điểm B₁(0; –b) và B₂(0; b) vào hình chữ nhật OA₂PB₂ thì $OP=\sqrt{a^2+b^2}=c$.

• Các điểm A₁, A₂ gọi là các đỉnh của hypebol.

• Đoạn thẳng A₁A₂ = 2a gọi là trục thực, đoạn thẳng B₁B₂ = 2b gọi là trục ảo của hypebol.

• Giao điểm O của hai trục là tâm đối xứng của hypebol.

• Nếu M(x; y) ∈ (H) thì x ≤ –a hoặc x ≥ a.

Ví dụ: Cho hypebol (H) có một tiêu điểm F₂(8; 0) và (H) đi qua điểm A(5; 0). Viết phương trình chính tắc của hypebol (H).

Hướng dẫn giải

Phương trình chính tắc của (H) có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, trong đó a, b > 0.

Vì A(5; 0) ∈ (H) nên ta có $\frac{5^2}{a^2}-\frac{0^2}{b^2}=1$. Suy ra a = 5.

Do (H) có một tiêu điểm F₂(8; 0) nên ta có c = 8.

Suy ra $b=\sqrt{c^2-a^2}=\sqrt{64-25}=\sqrt{39}$.

Vậy phương trình chính tắc của (H) là $\frac{x^2}{25}-\frac{y^2}{39}=1$.

3. Parabol

3.1. Nhận biết parabol

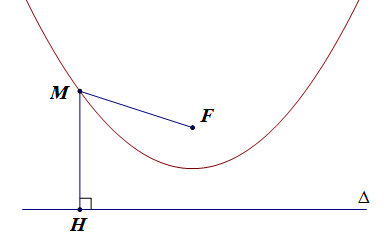
Cho một điểm F và một đường thẳng ∆ cố định không đi qua F. Parabol (P) là tập hợp các điểm M cách đều F và ∆.

F gọi là tiêu điểm và ∆ gọi là đường chuẩn của parabol (P).

3.2. Phương trình chính tắc của parabol

Cho parabol (P) có tiêu điểm F và đường chuẩn ∆. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p > 0.

Chọn hệ trục tọa độ Oxy sao cho $F\left(\frac{p}{2};0\right)$ và ∆: $x+\frac{p}{2}=0$.

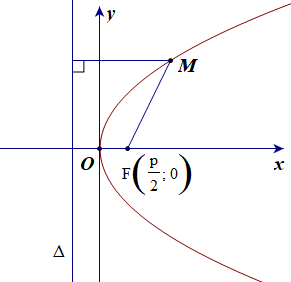
Người ta chứng minh được:

M(x; y) ∈ (P) ⇔ y² = 2px    (3).

Phương trình (3) gọi là phương trình chính tắc của parabol.

Chú ý:

• O gọi là đỉnh của parabol (P).

• Ox gọi là trục đối xứng của parabol (P).

• p gọi là tham số tiêu của parabol (P).

• Nếu M(x; y) ∈ (P) thì x ≥ 0 và M’(x; –y) ∈ (P).

Ví dụ: Viết phương trình chính tắc của parabol (P), biết (P) có đường chuẩn ∆: x + 4 = 0.

Hướng dẫn giải

(P) có đường chuẩn ∆: x + 4 = 0.

Ta suy ra $\frac{p}{2}=4$.

Khi đó p = 2.4 = 8.

Vậy phương trình chính tắc của parabol (P) là: y² = 16x.