Với giải Bài 5 trang 130 SBT Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải sách bài tập Toán lớp 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài 5 trang 130 SBT Toán 10 Tập 1: Khuê và Trọng ghi lại số tin nhắn điện thoại mà mỗi người nhận được từ ngày 1/9 đến ngày 15/9 năm 2020 ở bảng sau:

a) Hãy tìm phương sai của từng dãy số liệu.

b) Sau khi bỏ đi các giá trị ngoại lệ (nếu có), hãy so sánh, số lượng tin nhắn mỗi bạn nhận được theo số trung bình và theo trung vị.

Lời giải:

a) n = 15

+) Khuê:

Số trung bình cộng:

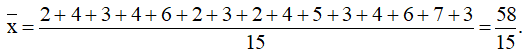
Phương sai:

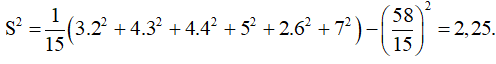
+) Trọng:

Số trung bình cộng:

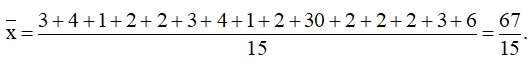
Phương sai:

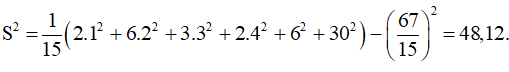
b)

+) Khuê:

Áp dụng các bước tìm tứ phân vị ta tìm được Q₁ = 3, Q₃ = 5

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 5 – 3 = 2.

Giá trị ngoại lệ x thỏa mãn

x > Q₃ + 1,5∆_Q = 5 + 1,5.2 = 8

Hoặc x < Q₁ − 1,5∆_Q = 3 − 1,5.2 = 0

Vậy đối chiếu mẫu số liệu của Khuê suy ra không có giá trị ngoại lệ.

+) Trọng:

Áp dụng các bước tìm tứ phân vị ta tìm được Q₁ = 2, Q₃ = 4

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 4 – 2 = 2.

Giá trị ngoại lệ x thỏa mãn

x > Q₃ + 1,5∆_Q = 4 + 1,5.2 = 7

Hoặc x < Q₁ − 1,5∆_Q = 2 − 1,5.2 = −1

Vậy đối chiếu mẫu số liệu của Trọng suy ra giá trị ngoại lệ là 30.

Sau khi bỏ đi giá trị ngoại lệ thì giá trị trung bình của mẫu của Khuê là:

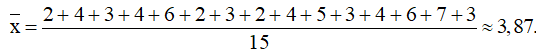
Và của Trọng là:

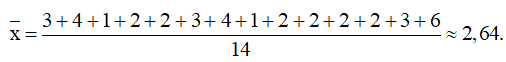
Khi đó trung vị của mẫu của Khuê là 4 (Với n = 15 là số lẻ)

Và số trung vị của Trọng là (2 + 2) : 2 = 2 (Với n = 14 là số chẵn).

Vậy so sánh theo cả số trung bình và số trung vị thì Khuê có nhiều tin nhắn mỗi ngày hơn Trọng.

Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1 trang 129 SBT Toán 10 Tập 1: Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ (nếu có) của mỗi mẫu số liệu sau:...

Bài 2 trang 129 SBT Toán 10 Tập 1: Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ (nếu có) của mỗi mẫu số liệu cho bởi bảng tần số sau:...

Bài 3 trang 129, 130 SBT Toán 10 Tập 1: Một kĩ thuật viên thống kê lại số lần máy bị lỗi từng ngày trong tháng 5/2021 ở bảng sau:...

Bài 4 trang 130 SBT Toán 10 Tập 1: Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn vị: °C)...

Bài 6 trang 130 SBT Toán 10 Tập 1: Bảng sau ghi giá bán ra lúc 11 giờ trưa của 2 mã cổ phiếu A và B trong 10 ngày liên tiếp (đơn vị: nghìn đồng)...

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài tập cuối chương 6

Bài 1: Dấu của tam thức bậc hai

Bài 2: Giải bất phương trình bậc hai một ẩn