Với giải Bài 4 trang 130 SBT Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải sách bài tập Toán lớp 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài 4 trang 130 SBT Toán 10 Tập 1: Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn vị: °C).

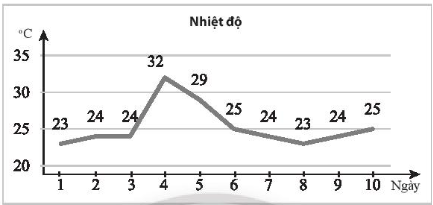
a) Hãy viết mẫu số liệu thống kê nhiệt độ từ biểu đồ trên.

b) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.

c) Hãy tìm phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải:

a) Ta có:

+) Nhiệt độ đạt 23°C tại các ngày: 1 và 8

+) Nhiệt độ đạt 24°C tại các ngày: 2, 3, 7 và 9

+) Nhiệt độ đạt 25°C tại các ngày: 6 và 10

+) Nhiệt độ đạt 29°C tại ngày: 5

+) Nhiệt độ đạt 32°C tại ngày: 4

Từ đó ta có mẫu số liệu thống kê nhiệt độ từ biểu đồ trên là

23; 24; 24; 32; 29; 25; 24; 23; 24; 25

b) Sắp xếp mẫu số liệu theo thứ tự không giảm:

23; 23; 24; 24; 24; 24; 25; 25; 29; 32

Khi đó, khoảng biến thiên R = 32 – 23 = 9.

Vì n = 10 là số chẵn nên ta có tứ phân vị thứ hai

Q₂ = (24 + 24) : 2 = 24.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 23; 23; 24; 24; 24.

Vậy Q₁ = 24.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 24; 25; 25; 29; 32.

Vậy Q₃ = 25.

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 25 – 24 = 1.

c) Số trung bình cộng:

$$\begin{gathered} \overline{x}=\frac{2.23+4.24+2.25+1.29+1.32}{10} \\ =25,3. \end{gathered}$$

Phương sai:

= 7,61

Khi đó độ lệch chuẩn S = $\sqrt{S^2}=\sqrt{7,61}\approx$2,76.

Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1 trang 129 SBT Toán 10 Tập 1: Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ (nếu có) của mỗi mẫu số liệu sau:...

Bài 2 trang 129 SBT Toán 10 Tập 1: Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ (nếu có) của mỗi mẫu số liệu cho bởi bảng tần số sau:...

Bài 3 trang 129, 130 SBT Toán 10 Tập 1: Một kĩ thuật viên thống kê lại số lần máy bị lỗi từng ngày trong tháng 5/2021 ở bảng sau:...

Bài 5 trang 130 SBT Toán 10 Tập 1: Khuê và Trọng ghi lại số tin nhắn điện thoại mà mỗi người nhận được từ ngày 1/9 đến ngày 15/9 năm 2020 ở bảng sau:...

Bài 6 trang 130 SBT Toán 10 Tập 1: Bảng sau ghi giá bán ra lúc 11 giờ trưa của 2 mã cổ phiếu A và B trong 10 ngày liên tiếp (đơn vị: nghìn đồng)...

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài tập cuối chương 6

Bài 1: Dấu của tam thức bậc hai

Bài 2: Giải bất phương trình bậc hai một ẩn