Với giải Bài 11 trang 72 Toán lớp 9 chi tiết trong Bài 2: Liên hệ giữa cung và dây giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 2: Liên hệ giữa cung và dây

Bài tập 11 trang 72 SGK Toán lớp 9 Tập 2: Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O').

a) So sánh các cung nhỏ BC, BD.

b) Chứng minh rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau: $\stackrel{⏜}{BE}=\stackrel{⏜}{BD}$).

Lời giải:

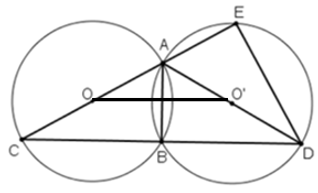
a)

Vì (O) và (O’) giao nhau tại A và B nên  $OO\text{'}\perp AB$ (1)

Xét tam giác ACD có:

O là trung điểm của AC (tâm – đường kính)

O’ là trung điểm của AD (tâm – đường kính)

Do đó, OO’ là đường trung bình

$\Rightarrow OO\text{'}\parallel CD$ (2)

Từ (1) và (2) ta suy ra $AB\perp CD$ tại B

Xét tam giác ACD có:

AC = AD (do đường tròn (O) bằng đường tròn (O’))

Do đó, tam giác ACD cân tại A

Ta có: $AB\perp CD$ tại B nên AB là đường cao và cũng là đường trung tuyến.

$\Rightarrow$ BC = BD

Mà đường tròn (O) và đường tròn (O’) bằng nhau

Do đó, cung nhỏ BC bằng cung nhỏ BD (theo định lý liên hệ cung và dây)

b) Xét đường tròn (O’)

Có: A, E, D cùng nằm trên (O’) và AD là đường kính

Do đó, tam giác AED vuông tại E

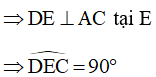
Xét tam giác DEC vuông tại E

Có: B là trung điểm của CD

Do đó, EB là đường trung tuyến ứng với cạnh huyền

$\Rightarrow EB=BD=BC=\frac{1}{2}DC$

Do đó, cung nhỏ EB bằng cung nhỏ BD (theo định lí liên hệ cung và dây)

Vậy điểm B là điểm chính giữa của cung EBD.