Với giải Bài 13 trang 72 Toán lớp 9 chi tiết trong Bài 2: Liên hệ giữa cung và dây giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 2: Liên hệ giữa cung và dây

Bài tập 13 trang 72 SGK Toán lớp 9 Tập 2: Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Lời giải

TH1: Tâm O nằm ngoài hai dây cung song song.

Kẻ hai dây cung AB // CD

Kẻ đường kính MN // AB // CD

Do MN // AB nên ta có:

$\widehat{OAB}=\widehat{AOM}$ (1)  (hai góc so le trong)

$\widehat{OBA}=\widehat{BON}$ (2) (hai góc so le trong)

Xét tam giác OAB có:

OA = OB (cùng bằng bán kính đường tròn tâm O)

Do đó, tam giác OAB cân tại O

$\Rightarrow \widehat{OAB}=\widehat{OBA}$  (3) (tính chất tam giác cân)

Từ (1), (2), (3) ta suy ra: $\widehat{AOM}=\widehat{BON}$

Mà ta có:

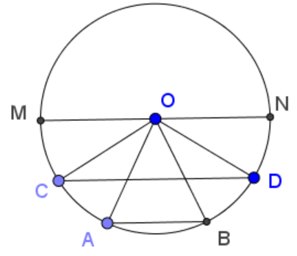
Góc AOM chắn cung nhỏ MCA

Góc BON chắn cung nhỏ NDB

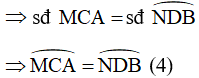
Ta có: MN // CD

$\Rightarrow \widehat{MOC}=\widehat{OCD}$ (5) (hai góc so le trong) ; $\widehat{NOD}=\widehat{ODC}$ (6) (hai góc so le trong)

Xét tam giác OCD có:

OC = OD (cùng bằng bán kính đường tròn tâm O)

Do đó, tam giác OCD cân tại O

$\Rightarrow \widehat{OCD}=\widehat{ODC}$ (7) (tính chất tam giác cân)

Từ (5), (6), (7) ta suy ra: $\widehat{MOC}=\widehat{NOD}$

Mà ta có:

Góc MOC chắn cung nhỏ MC

Góc NOD chắn cung nhỏ ND

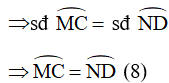
Mặt khác, ta có: C nằm trên cung nhỏ MCA và D nằm trên cung nhỏ NDB (9)

Từ (4), (8), (9) ta suy ra:

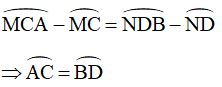
Vậy hai cung bị chắn giữa hai dây song song thì bằng nhau.

TH2: O nằm giữa hai dây cung song song

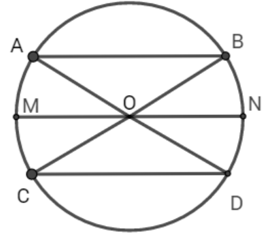
Kẻ hai dây cung AB // CD

Kẻ đường kính MN // AB // CD

Do MN // AB nên ta có:

$\widehat{MOA}=\widehat{OAB}$ (1) (hai góc so le trong)

$\widehat{OBA}=\widehat{BON}$ (2) (hai góc so le trong)

Xét tam giác OAB có:

OA = OB (cùng bằng bán kính đường tròn tâm O)

Do đó, tam giác OAB cân tại O

$\Rightarrow \widehat{OAB}=\widehat{OBA}$  (3) (tính chất tam giác cân)

Từ (1), (2), (3) ta suy ra:  $\widehat{MOA}=\widehat{BON}$

Mà ta có:

Góc MOA chắn cung nhỏ AM

Góc BON chắn cung nhỏ BN

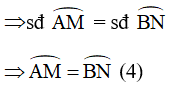
Do  MN // CD nên ta có:

$\widehat{MOC}=\widehat{OCD}$ (5) ( hai góc so le trong)

$\widehat{NOD}=\widehat{ODC}$ (6) ( hai góc so le trong)

Xét tam giác OCD có:

OC = OD (cùng bằng bán kính đường tròn tâm O)

Do đó, tam giác OCD cân tại O

$\Rightarrow \widehat{OCD}=\widehat{ODC}$ (7) (tính chất tam giác cân)

Từ (5), (6), (7) ta suy ra: $\widehat{MOC}=\widehat{NOD}$

Mà ta có:

Góc MOC chắn cung nhỏ MC

Góc NOD chắn cung nhỏ DN

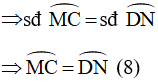
Mặt khác, ta có: M nằm trên cung nhỏ AC, N nằm trên cung nhỏ BD (9)

Từ (4), (8), (9) ta suy ra:

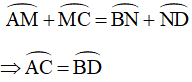
 Vậy hai cung bị chắn giữa hai dây song song thì bằng nhau.