Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 3 Bài 2: Liên hệ giữa cung và dây. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 2: Liên hệ giữa cung và dây. Mời các bạn đón xem:
Bài tập Toán 9 Chương 3 Bài 2: Liên hệ giữa cung và dây
A. Bài tập Liên hệ giữa cung và dây
I. Bài tập trắc nghiệm
Câu 1: Cho đường tròn (O) có hai dây AB, CD song song với nhau. Kết luận nào sau đây là đúng?
A. AD > BC
B. Số đo cung AD bằng số đo cung BC
C. AD < BC
D. Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án
Lời giải:
Qua O kẻ đường thẳng vuông góc với AB và CD, cắt AB, CD lần lượt tại H và K.
Phương án A, C, D sai, B đúng
Chọn đáp án B
Câu 2: Chọn khẳng định đúng. Cho đường tròn (O) có dây cung AB > CD khi đó
A. Cung AB lớn hơn cung CD
B. Cung AB nhỏ hơn cung CD
C. Cung AB bằng cung CD
D. Số đo cung AB bằng hai lần số đo cung BC
Lời giải:
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau
+ Cung lớn hơn căng dây lớn hơn
+ Dây lớn hơn căng cung lớn hơn
Nên dây AB > CD thì cung AB lớn hơn cung CD
Chọn đáp án A
Câu 3: Cho đường tròn (O) đường kính AB và một cung AC có số đo nhỏ hơn 90°. Vẽ dây CD vuông góc với AB và dây DE song song với AB . Chọn kết luận sai?
A. AC = BE
B. Số đo cung AD bằng số đo cung BE
C. Số đo cung AC bằng số đo cung BE
D. Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án
Lời giải:
Chọn đáp án D
Câu 4: Chọn khẳng định đúng.
A. Trong một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
B. Trong một đường tròn, đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
C. Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì song song với dây căng cung ấy
D. Trong một đường tròn, hai đường kính luôn vuông góc với nhau
Lời giải:
+ Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy
+ Trong một đường tròn, đường kính đi qua trung điểm của một dây (không qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy
+ Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông với dây căng cung ấy và ngược lại
Chọn đáp án A.
Câu 5: Cho tam giác ABC cân tại A có A^= 66° nội tiếp đường tròn (O) . Trong các cung nhỏ AB, BC, CA thì cung nào là cung lớn nhất?
A. AB
B. AC
C. BC
D. AB, AC
Lời giải:
nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có:
Chọn đáp án C.
Câu 6: Cho nửa đường tròn (O) đường kính AB. Lấy các điểm C và D trên nửa đường tròn sao cho: 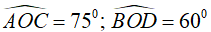
CD < BD < CA
Ta có:
Chọn đáp án D.
Câu 7: Cho đường tròn (O) ngoại tiếp tam giác ABC biết rằng A^= 60° và AB = BC .Tìm khẳng định sai ?
Ta có: AB = BC nên tam giác ABC cân tại B.
Chọn đáp án A.
Câu 8: Cho tam giác ABC nội tiếp đường tròn (O) sao cho 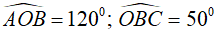
Chọn đáp án C.
Câu 9: Cho nửa đường tròn (O) đường kính AB, điểm C và D nằm trên nửa đường tròn sao cho 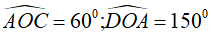
D. Tìm khẳng định đúng
Chọn đáp án A.
Câu 10: Cho tam giác ABC nội tiếp đường tròn tâm (O), biết rằng AB = BC = 8cm và 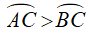
Ta có:
Chọn đáp án B.
Câu 11: Cho đường tròn (O; R) và hai dây AB; CD sao cho 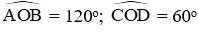
A. CD = 2AB
B. AB > 2CD
C. CD > AB
D. CD < AB < 2CD
Vì 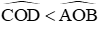
Xét tam giác OCD cân tại O có 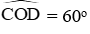
⇒ CD = R
AB là dây không đi qua tâm nên AB < 2R ⇒ AB < 2CD (**)
Từ (*) và (**) ta có CD < AB < 2CD
Đáp án cần chọn là: D
Câu 12: Cho đường tròn (O; R) và hai dây MN; EF sao cho 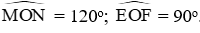
A. MN = 2R
B. MN < 2R
C. R√2 < MN
D. Cả B, C đều đúng
Vì 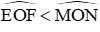
Xét tam giác OEF cân tại O có 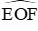
EF2 = OF2 + OE2 = R2 + R2 = 2R2 ⇒ EF = R√2 (**)
MN là dây không đi qua tâm nên MN < 2R (***)
Từ (*), (**) và (***) ta có R√2 < MN < 2R
Đáp án cần chọn là: D
Câu 13: Cho tam giác ABC có 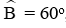
A. Cung HB nhỏ nhất
B. Cung MB lớn nhất
C. Cung MH nhỏ nhất
D. Ba cung bằng nhau
Vì trong một đường tròn hai cung bằng nhau căng hai dây bằng nhau nên ta đi so sánh các đoạn thẳng HB; MB; MH
Xét tam giác BCH vuông tại H có:
Xét tam giác HBM có BM = BH (cmt) và 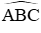
⇒ BM = BH = HM
Suy ra ba cung HB; MB; MH bằng nhau
Đáp án cần chọn là: D
Câu 14: Cho tam giác ABC có 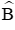
A. Cung HB lớn nhất
B. Cung HB nhỏ nhất
C. Cung MH nhỏ nhất
D. Cung MB = cung MH
Vì trong một đường tròn hai cung bằng nhau căng hai dây bằng nhau nên ta đi so sánh các đoạn thẳng HB; MB; MH
Xét tam giác BCH vuông tại H có:
Xét tam giác HBC vuông tại H có HM là trung tuyến ứng với cạnh huyền nên HM = BM = CM = 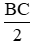
Mà 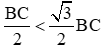
Suy ra cung MB = cung HM < cung HB
Hay cung HB là cung lớn nhất nên B sai
Đáp án cần chọn là: B
Câu 15: Cho đường tròn (O; R), dây cung AB = R√3. Vẽ đường kính CD AB (C thuộc cung lớn AB). Trên cung AC nhỏ lấy điểm M, vẽ dây AN // CM. Độ dài đoạn MN là:
Lời giải:
Vì hai dây MC // AN nên hai cung AM và cung CN bằng nhau hay AM = CN
Suy ra MCNA là hình thang cân ⇒ MN = AC
Gọi H là giao của CD và AB. Khi đó vì AB ⊥ CD tại H nên H là trung điểm của AB
Xét tam giác vuông AHO, theo định lý Pytago ta có:
Theo định lý Pytago cho tam giác ACH vuông ta có:
Đáp án cần chọn là: A
II. Bài tập tự luận có lời giải
Câu 1: Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O). Biết ∠A = 50°, hãy so sánh các cung nhỏ AB, AC và BC.
Lời giải:
Ta có: ΔABC cân tại A và ∠A = 50°
Khi đó
III. Bài tập vận dụng
Bài 1: Dựa vào hình vẽ sau, hãy so sánh AB và CD:
Bài 2: Cho (O) có dây cung BC cố định. Gọi A là điểm thuộc cung lớn BC sao cho 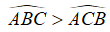
B. Lý thuyết Liên hệ giữa cung và dây
1. Định lí 1
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
- Hai cung bằng nhau căng hai dây bằng nhau.
- Hai dây bằng nhau căng hai cung bằng nhau.
Ví dụ 1. Cho đường tròn (O) như hình vẽ.
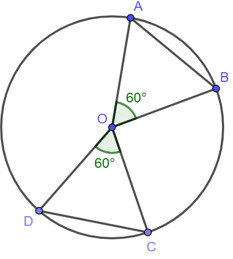
Trong hình vẽ (![]() ) nên AB = CD.
) nên AB = CD.
2. Định lí 2
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
- Cung lớn hơn căng dây lớn hơn.
- Dây lớn hơn căng cung lớn hơn.
Ví dụ 2. Cho đường tròn (I) như hình vẽ.
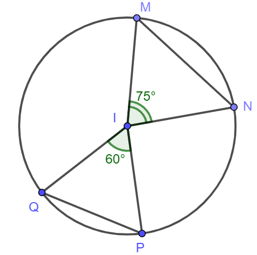
Trong hình vẽ :
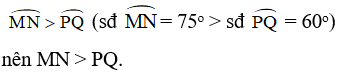
3. Bổ sung
Trong một đường tròn:
- Hai cung bị chắn giữa hai dây song song thì bằng nhau.
- Đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
- Đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
- Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.