Trong Hình 3.37 có BE // AC, CF //AB. Biết góc A = 80 độ, góc ABC = 60 độ

Với giải Bài 3.37 trang 50 SBT Toán lớp 7 Kết nối tri thức chi tiết trong Ôn tập chương 3 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải sách bài tập Toán lớp 7 Ôn tập chương 3

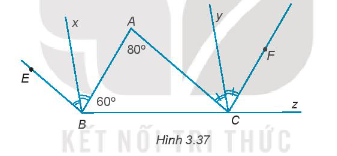
Bài 3.37 trang 50 SBT Toán 7 Tập 1: Trong Hình 3.37 có BE // AC, CF //AB. Biết $\hat{A} = 80 °; \hat{A B C} = 60 °$ .

a) Chứng minh rằng $\hat{A B E} = \hat{A C F}$ .

b) Tính số đo của các góc BCF và ACB.

c) Gọi Bx, Cy lần lượt là tia phân giác của các góc BE và ACF. Chứng minh rằng Bxx // Cy.

Sách bài tập Toán 7 Ôn tập chương 3 - Kết nối tri thức (ảnh 1)

Lời giải:

a) Vì BE song song với AC nên các góc so le trong bằng nhau.

Do đó, $\hat{A B E} = \hat{A} = 80 °$ (hai góc so le trong) (1)

Vì CF song song với AB nên các góc so le trong bằng nhau.

Do đó, $\hat{A C F} = \hat{A} = 80 °$ (hai góc so le trong) (2)

Từ (1) và (2) suy ra $\hat{A B E} = \hat{A C F}$ = 80^o.

b) Vì CF song song với AB nên các góc đồng vị bằng nhau.

Do đó, $\hat{A B C}$ = $\hat{F C z}$ (hai góc đồng vị)

Do đó, $\hat{A B C}$ = $\hat{F C z}$ = 60^o.

Ta có, $\hat{B C F}$ và $\hat{F C z}$ là hai góc kề bù nên $\hat{B C F}$ + $\hat{F C z}$ = 180^o.

Thay số , $\hat{B C F}$ + 60^o = 180^o

$\hat{B C F}$ = 180^o – 60^o

$\hat{B C F}$ = 120^o.

Ta có:

$\hat{B C F}$ = $\hat{A C F}$ + $\hat{A C B}$

120^o = 80^o + $\hat{A C B}$

$\hat{A C B}$ = 120^o – 80^o

$\hat{A C B}$ = 40^o.

Vậy $\hat{A C B}$ = 40^o; $\hat{B C F}$ = 120^o.

c) Vì Bx là tia phân giác của góc $\hat{A B E}$ nên $\hat{E B x} = \hat{x B A} = \frac{\hat{E B A}}{2} = \frac{80 °}{2} = 40 °$

Vì Cy là tia phân giác của góc $\hat{A C F}$ nên $\hat{A C y} = \hat{y C F} = \frac{\hat{A C F}}{2} = \frac{80 °}{2} = 40 °$

Ta có BC cắt Bx và cắt Cy tạo ra cặp góc đồng vị là $\hat{z C y}$ và $\hat{z B x}$ .

Ta có:

$\hat{z C y}$ = $\hat{y C F}$ + $\hat{F C z}$ = 40^o + 60^o = 100^o.

$\hat{z B x}$ = $\hat{x B A}$ + $\hat{A B C}$ = 40^o + 60^o = 100^o.

Suy ra, $\hat{z C y}$ = $\hat{z B x}$ = 100^o

Vì $\hat{z C y}$ và $\hat{z B x}$ là hai góc đồng vị và $\hat{z C y}$ = $\hat{z B x}$ nên Bx // Cy.

Xem thêm các bài giải SBT Toán 7 Kết nối tri thức hay, chi tiết khác:

Câu hỏi 1 trang 47 SBT Toán 7 Tập 1: Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?...

Câu hỏi 2 trang 47 SBT Toán 7 Tập 1: Trong các khẳng định sau, khẳng định nào đúng?...

Câu hỏi 3 trang 47 SBT Toán 7 Tập 1: Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là 65^o. Khi đó số đo của ba góc còn lại là:...

Câu hỏi 4 trang 47 SBT Toán 7 Tập 1: Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?...

Câu hỏi 5 trang 47 SBT Toán 7 Tập 1: Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và $\hat{B O M} = 30 °$ . Số đo của góc AOC bằng:...

Câu hỏi 6 trang 48 SBT Toán 7 Tập 1: Cho Hình 3.29...

Câu hỏi 7 trang 48 SBT Toán 7 Tập 1: Cho Hình 3.30. Cặp góc A₁; B₁ là cặp góc:...

Câu hỏi 8 trang 48 SBT Toán 7 Tập 1: Cho Hình 3.31, đường thẳng a song song với đường thẳng b nếu:...

Câu hỏi 9 trang 48 SBT Toán 7 Tập 1: Cho Hình 3.32, biết a // b. Khẳng địn nào sau đây là sai?...

Bài 3.33 trang 49 SBT Toán 7 Tập 1: Cho Hình 3.33. Hãy chứng minh xy // x’y’...

Bài 3.34 trang 49 SBT Toán 7 Tập 1: Cho Hình 3.34. Biết AB // Cx, $\hat{A} = 70 °; \hat{B} = 60 °$ ...

Bài 3.35 trang 49 SBT Toán 7 Tập 1: Cho Hình 3.35. Biết CN là tia phân giác của góc ACM...

Bài 3.36 trang 50 SBT Toán 7 Tập 1: Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox song song với AB. Biết $\hat{B} = 40 °; \hat{D} = 70 °; \hat{B O D} = 110 °$ ...

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 11: Định lí và chứng minh định lí

Ôn tập chương 3

Bài 12: Tổng các góc trong một tam giác

Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Trong Hình 3.37 có BE // AC, CF //AB. Biết góc A = 80 độ, góc ABC = 60 độ

Từ khóa :

Đánh giá

Bài viết cùng môn học

Tìm kiếm

Bài Viết Xem Nhiều