Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức, chi tiết nhất giúp học sinh dễ dàng làm bài tập Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức lớp 8.
Giải bài tập Toán lớp 8 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 20 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử
a) ;
b) .
Phương pháp giải: Áp dụng hằng đẳng thức số
Lời giải:
a)
b)
Trả lời câu hỏi 2 trang 20 sgk Toán 8 Tập 1: Tính nhanh:
Phương pháp giải: Áp dụng hằng đẳng thức số .
Lời giải:
Câu hỏi và bài tập (trang 20, 21 sgk Toán 8 Tập 1)
Bài 43 trang 20 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
a) ;
b);
c) ;
d)
Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ:
Lời giải:
a)
b)
c)
d)
Bài 44 trang 20 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
a) ;
b) ;
c) ;
d) ;
e)
Lời giải:
a)
Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Tổng hai lập phương.
Lời giải:
b)
Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ: Hiệu hai lập phương, bình phương một tổng, bình phương một hiệu, hiệu hai bình phương.
Lời giải:
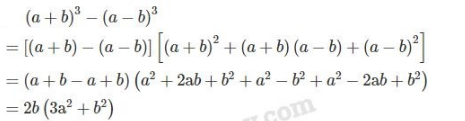
c)
Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ: Tổng hai lập phương, bình phương một tổng, bình phương một hiệu, hiệu hai bình phương.
Lời giải:
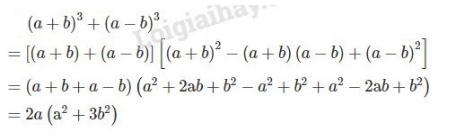
d)
Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Lập phương một tổng.
Lời giải:
e)
Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Lập phương một hiệu.
Lời giải:
Bài 45 trang 20 sgk Toán 8 Tập 1: Tìm , biết:
a) ;
b)
Lời giải:
a)
Phương pháp giải: - Phân tích các biểu thức ở vế trái thành nhân tử, sau đó áp dụng tính chất:
hoặc
- Áp dụng hằng đẳng thức hiệu hai bình phương.
Lời giải:
hoặc
+) Với
+) Với
Vậy hoặc
Cách khác:
hoặc
hoặc
b)
Phương pháp giải: - Phân tích các biểu thức ở vế trái thành nhân tử, sau đó áp dụng tính chất:
hoặc
- Áp dụng hằng đẳng thức bình phương một hiệu.
Lời giải:
Vậy
Bài 46 trang 21 sgk Toán 8 Tập 1: Tính nhanh:
a) ;
b) ;
c) .
Phương pháp giải: Áp dụng hằng đẳng thức hiệu hai bình phương để phân tích các đa thức đó thành nhân tử.
Lời giải:
a)
b)
c)
.
Lý thuyết Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
1. Các kiến thức cần nhớ: Ta sử dụng các hằng đẳng thức đáng nhớ đã học để thực hiện phép phân tích đa thức thành nhân tử.
Các hằng đẳng thức đáng nhớ:
.
.
.
.
.
.
.
Ví dụ:
Chú ý: Khi áp dụng phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử, ta cần lưu ý:
- Trước tiên nhận xét xem các hạng tử của đa thức có chứa nhân tử chung không ? Nếu có thì áp dụng phương pháp đặt thành nhân tử chung.
- Nếu không thì xét xem có thể áp dụng hằng đẳng thức đáng nhớ để phân tích thành nhân tử hay không ?
Chú ý: Đôi khi phải dùng quy tắc dấu ngoặc sau đó mới áp dụng được hằng đẳng thức.
Ví dụ:
2. Các dạng toán thường gặp:
Dạng 1: Phân tích đa thức thành nhân tử
Phương pháp: Ta sử dụng các hằng đẳng thức đã học để phân tích đa thức đã cho thành nhân tử.
Dạng 2: Tìm
Phương pháp: Ta sử dụng các hằng đẳng thức đã học để phân tích đa thức đã cho thành nhân tử.
Từ đó đưa về dạng tìm thường gặp như
Dạng 3: Tính giá trị biểu thức thỏa mãn điều kiện cho trước
Phương pháp: Ta biến đổi biểu thức đã cho để có thể sử dụng được điều kiện ở giả thiết. Từ đó tính giá trị biểu thức.