Giải SBT Toán 10 trang 108 Tập 1 Cánh diều

Nguyễn Mạnh Tài Ngày: 23-11-2022 Lớp 10

524

Với lời giải SBT Toán 10 trang 108 Tập 1 chi tiết trong Bài ôn tập chương 4 sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài ôn tập chương 4

Bài 79 trang 108 SBT Toán 10 Tập 1: a) Chứng minh đẳng thức ${|\vec{a} + \vec{b}|}^{2} = {|\vec{a}|}^{2} + {|\vec{b}|}^{2} + 2. \vec{a} . \vec{b}$ với $\vec{a}$ và $\vec{b}$ là hai vectơ bất kì.

b) Cho $|\vec{a}| = 2, |\vec{b}| = 3, |\vec{a} + \vec{b}| = \sqrt{7}$ . Tính $\vec{a} . \vec{b}$ và $(\vec{a}, \vec{b})$ .

Lời giải:

${|\vec{a} + \vec{b}|}^{2} = {(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + {\vec{b}}^{2} + 2. \vec{a} . \vec{b} = {|\vec{a}|}^{2} + {|\vec{b}|}^{2} + 2. \vec{a} . \vec{b}$

b) Áp dụng công thức trên ta được:

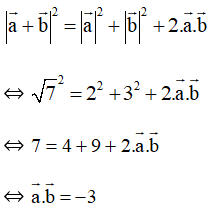
Sách bài tập Toán 10 Bài ôn tập chương 4 - Cánh diều (ảnh 1)

Mặt khác ta lại có:

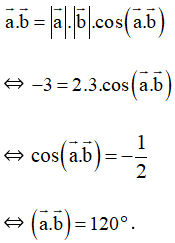
Sách bài tập Toán 10 Bài ôn tập chương 4 - Cánh diều (ảnh 1)

Vậy $\vec{a} . \vec{b} = - 3$ và $(\vec{a} . \vec{b}) = 120 °$ .

Bài 80 trang 108 SBT Toán 10 Tập 1: Cho tam giác ABC, có ba trung tuyến AD, BE, CF. Chứng minh rằng: $\vec{A D} . \vec{B C} + \vec{B E} . \vec{C A} + \vec{C F} . \vec{A B} = 0$ .

Lời giải:

Ta có: $\vec{A D} . \vec{B C} + \vec{B E} . \vec{C A} + \vec{C F} . \vec{A B}$

= $\frac{1}{2} (\vec{A B} + \vec{A C}) . \vec{B C} + \frac{1}{2} (\vec{B A} + \vec{B C}) .$ $\vec{C A} + \frac{1}{2} (\vec{C A} + \vec{C B}) . \vec{A B}$

= $\frac{1}{2} \vec{A B} . \vec{B C} + \frac{1}{2} \vec{A C} . \vec{B C} + \frac{1}{2} \vec{B A} . \vec{C A}$ $+ \frac{1}{2} \vec{B C} . \vec{C A} + \frac{1}{2} \vec{C A} . \vec{A B} + \frac{1}{2} \vec{C B} . \vec{A B}$

= $(\frac{1}{2} \vec{A B} . \vec{B C} + \frac{1}{2} \vec{C B} . \vec{A B}) +$ $(\frac{1}{2} \vec{A C} . \vec{B C} + \frac{1}{2} \vec{B C} . \vec{C A}) +$ $(\frac{1}{2} \vec{B A} . \vec{C A} + \frac{1}{2} \vec{C A} . \vec{A B})$

= 0

Bài 81 trang 108 SBT Toán 10 Tập 1: Cho tứ giác ABCD, M là điểm thay đổi trong mặt phẳng thỏa mãn $(\vec{M A} + \vec{M B}) . (\vec{M C} + \vec{M D}) = 0$ . Chứng minh M luôn nằm trên đường tròn cố định.

Lời giải:

Gọi I và J lần lượt là trung điểm của AB và CD.

Khi đó ta có: $\vec{I A} + \vec{I B} = \vec{0}$ và $\vec{J C} + \vec{J D} = \vec{0}$

⇒ $(\vec{M A} + \vec{M B}) . (\vec{M C} + \vec{M D}) =$ $(\vec{M I} + \vec{I A} + \vec{M I} + \vec{I B})$ $. (\vec{M J} + \vec{J C} + \vec{M J} + \vec{J D}) = \vec{0}$

⇔ $(\vec{M I} + \vec{I A} + \vec{M I} + \vec{I B}) .$ $(\vec{M J} + \vec{J C} + \vec{M J} + \vec{J D}) = \vec{0}$

⇔ $(2 \vec{M I} + \vec{I A} + \vec{I B}) . (2 \vec{M J} + \vec{J C} + \vec{J D}) = \vec{0}$

⇔ $4 \vec{M I} . \vec{M J} = \vec{0}$

⇔ $\hat{IMJ} = 90 °$

Vậy M là điểm thuộc đường tròn đường kính IJ.

Bài 82 trang 108 SBT Toán 10 Tập 1: Cho tam giác ABC và đường thẳng d không có điểm chung với bất kì cạnh nào của tam giác. M là điểm thay đổi trên đường thẳng d. Xác định vị trí của M sao cho biểu thức $|\vec{M A} + \vec{M B} + \vec{M C}|$ đạt giá trị nhỏ nhất.

Lời giải:

Xét biểu thức $\vec{M A} + \vec{M B} + \vec{M C} = \vec{M G} + \vec{G A} +$ $\vec{M G} + \vec{G B} + \vec{M G} + \vec{G C}$

$= 3 \vec{M G} + (\vec{G A} + \vec{G B} + \vec{G C})$

$= 3 \vec{M G}$

⇒ $|\vec{M A} + \vec{M B} + \vec{M C}| = |3 \vec{M G}|$

Do đó để biểu thức $|\vec{M A} + \vec{M B} + \vec{M C}|$ đạt giá trị nhỏ nhất thì $|3 \vec{M G}|$ đạt giá trị nhỏ nhất khi MG nhỏ nhất và MG nhỏ nhất khi M là hình chiếu vuông góc của G lên đường thẳng d.