Với lời giải SBT Toán 10 trang 75 Tập 1 chi tiết trong Bài 2: Định lí côsin và định lí sin sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 2: Định lí côsin và định lí sin

Bài 3 trang 75 SBT Toán 10 Tập 1: Tìm góc lớn nhất của tam giác ABC, biết a = 8, b = 12, c = 6.

Lời giải

Do b là cạnh lớn nhất nên B là góc lớn nhất.

Theo định lí côsin: b² = a² + c² – 2accosB

⇒ cosB = $\frac{{\text{a}}^2+{\text{c}}^2-{\text{b}}^2}{2\text{ac}}$ = $\frac{8^2+6^2-{12}^2}{\mathrm{2.8.6}}$

⇒ cosB = $\frac{-11}{24}$.

⇒ $\widehat{\text{B}}$ = 117°16’46’’.

Vậy góc lớn nhất của tam giác ABC là  = 117°16’46’’.

Bài 4 trang 75 SBT Toán 10 Tập 1: Tính khoảng cách giữa hai điểm P và Q của một hồ nước ( Hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400m và 600m người quan sát nhìn thấy một góc 76°.

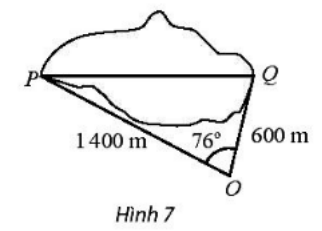
Lời giải

Áp dụng định lí côsin:

PQ² = OP² + OQ² – 2.OP.OQ.cos$\hat{O}$

PQ² = 1400² + 600² – 2.1400.600.cos76°

PQ = $\sqrt{{1400}^2+{600}^2–\mathrm{2.1400.600.}\text{cos}76°}$

PQ ≈ 1383,32 (m).

Vậy khoảng cách giữa hai điểm PQ là PQ ≈ 1383,32 (m).

Bài 5 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC với BC = a; AC = b; AB = c. Chứng minh rằng: 1 + cosA = $\frac{(\text{a}+\text{b}+\text{c})(-\text{a}+\text{b}+\text{c})}{2\mathrm{bc}}$.

Lời giải

Theo định lí côsin ta có: a² = b² + c² – 2bccosA

⇒ cosA = $\frac{{\text{b}}^2+{\text{c}}^2-{\text{a}}^2}{\text{2bc}}$

Ta có:

1 + cosA = 1 + $\frac{{\text{b}}^2+{\text{c}}^2-{\text{a}}^2}{\text{2bc}}$ 

= $\frac{2\text{bc}+{\text{b}}^2+{\text{c}}^2-{\text{a}}^2}{2\text{bc}}$ 

= $\frac{{(\text{b}+\text{c})}^2-{\text{a}}^2}{2\text{bc}}$ 

= $\frac{(\text{a}+\text{b}+\text{c})(-\text{a}+\text{b}+\text{c})}{2\mathrm{bc}}$

Vậy ta có điều phải chứng minh.

Bài 6 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có a = 24cm, b = 26cm, c = 30cm.

a) Tính diện tích tam giác ABC.

b) Tính bán kính đường tròn nội tiếp tam giác ABC.

Lời giải

a) Ta có: p = $\frac{\text{a}+\text{b}+\text{c}}{2}$ = $\frac{24+26+30}{2}$ = 40

Áp dụng công thức Heron:

S = $\sqrt{\text{p}.(\text{p}-\text{a}).(\text{p}-\text{b}).(\text{p}-\text{c})}$

S = $\sqrt{40.(40-24).(40-26).(40-30)}$

S = 80$\sqrt{14}$(cm²).

Vậy diện tích tam giác ABC là 80$\sqrt{14}$(cm²).

b) Ta có: S = p.r = 40r = 80$\sqrt{14}$

⇒ r = 2$\sqrt{14}$(cm).

Vậy bán kính đường tròn nội tiếp tam giác ABC là r = 2$\sqrt{14}$cm.

Bài 7 trang 75 SBT Toán 10 Tập 1: Cho tam giác MNP có MN = 10, MP = 20 và $\hat{M}$= 42°.

a) Tính diện tích tam giác MNP.

b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP.

Lời giải

a) Diện tích tam giác MNP là:

S = $\frac{1}{2}$.MN.MP.sin$\hat{M}$= $\frac{1}{2}$.10.20.sin42° ≈ 67 (đvdt).

Vậy diện tích tam giác MNP là 67 đvdt.

b)

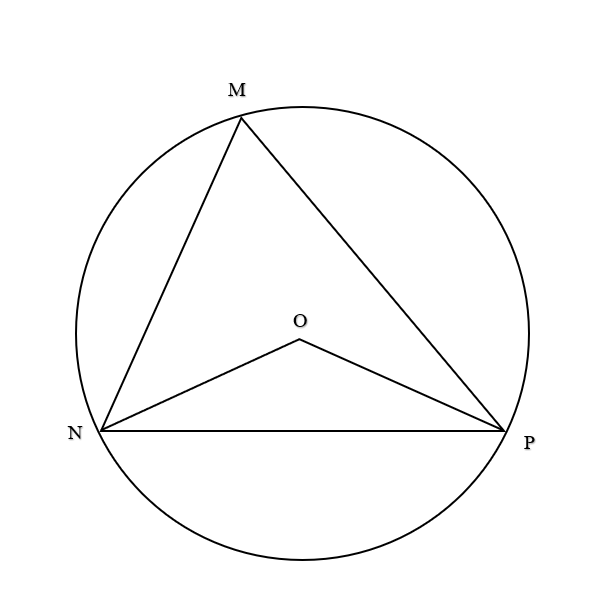
Áp dụng định lí côsin:

NP² = MP² + MN² – 2.MN.MP.cos$\hat{M}$

NP² = 10² + 20² – 2.10.20.cos42°

NP = $\sqrt{{10}^2+{20}^2–\mathrm{2.10.20.}\text{cos}42°}$

NP ≈ 14,24.

Áp dụng định lí sin trong tam giác MNP, ta có: R = ON = OP = $\frac{\text{NP}}{\text{2sin}\widehat{\text{M}}}$ ≈ $\frac{14,24}{2\sin 42°}$ ≈ 10,64

Xét đường tròn tâm O ngoại tiếp tam giác MNP:

$\widehat{\text{NMP}}$ là góc nội tiếp chắn cung NP ⇒ $\widehat{\text{NMP}}$ = $\frac{1}{2}\widehat{\text{NOP}}$ ⇒ $\widehat{\text{NOP}}$ = 42°.2 = 84°.

Suy ra S_ONP = $\frac{1}{2}$.ON.OP.sin$\widehat{\text{NOP}}$ ≈ $\frac{1}{2}$.(10,64)².sin84° ≈ 56,30 (đvdt)

Vậy diện tích tam giác ONP là 56,30 đvdt.

Bài 8 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau.

Lời giải

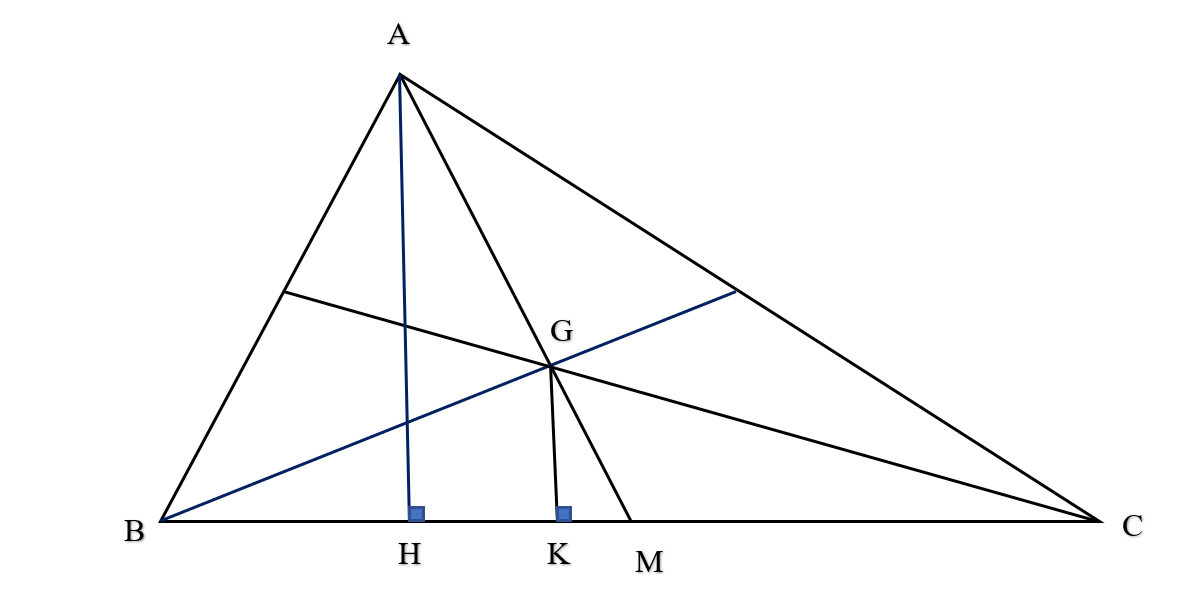
Vẽ AH và GK vuông góc với BC.

Gọi M là chân đường trung tuyến từ A hạ xuống BC. Ta có GM = AM ( tính chất đường trung tuyến của tam giác).

Xét tam giác GKM và tam giác AHM:

$\widehat{\text{AHM}}$ = $\widehat{\text{GKM}}$ = 90°

$\widehat{\text{AMH}}$ = $\widehat{\text{GMK}}$ 

⇒ tam giác GKM và tam giác AHM đồng dạng (g.g).

⇒ $\frac{\text{GM}}{\text{AM}}=\frac{\text{GK}}{\text{AH}}=\frac{1}{3}$

Có $\frac{{\text{S}}_{\text{GBC}}}{{\text{S}}_{\text{ABC}}\text{}}\text{ = }\frac{\frac{\text{1}}{\text{2}}\text{.GK.BC}}{\frac{\text{1}}{\text{2}}\text{.AH.BC}}$ = $\frac{\text{GK}}{\text{AH}}=\frac{1}{3}$.

Chứng minh tương tự ta được:

S_GBC = S_GAB = S_GAC = $\frac{1}{3}$S_ABC. ( ĐPCM).

Bài 9 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC và các điểm B’, C’ trên cạnh AB và AC. Chứng minh: $\frac{{\text{S}}_{\text{ABC}}}{{\text{S}}_{\text{AB'C'}}}\text{ = }\frac{\text{AB.AC}}{\text{AB'.AC'}}$.

Lời giải

Ta có:

S_ABC = $\frac{1}{2}$.AB.AC.sin$\hat{A}$

S_AB’C’ = $\frac{1}{2}$.AB’.AC’.sin$\hat{A}$

⇒ $\frac{{\text{S}}_{\text{ABC}}}{{\text{S}}_{\text{AB'C'}}}$ = $\frac{\frac{\text{1}}{\text{2}}\text{.AB.AC.sin}\widehat{\text{A}}}{\frac{1}{2}\text{.AB’.AC’.sin}\widehat{\text{A}}}$

⇒ $\frac{{\text{S}}_{\text{ABC}}}{{\text{S}}_{\text{AB'C'}}}\text{ = }\frac{\text{AB.AC}}{\text{AB'.AC'}}$ (ĐPCM).

Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 74 Tập 1

Giải SBT Toán 10 trang 76 Tập 1

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Giá trị lượng giác của một góc từ 0 đến 180

Bài 2: Định lí côsin và định lí sin

Bài 3: Giải tam giác và ứng dụng thực tế

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ