Với giải sách bài tập Toán 7 Bài tập cuối chương 5 sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài tập cuối chương 5
Giải SBT Toán 7 trang 25 Tập 2
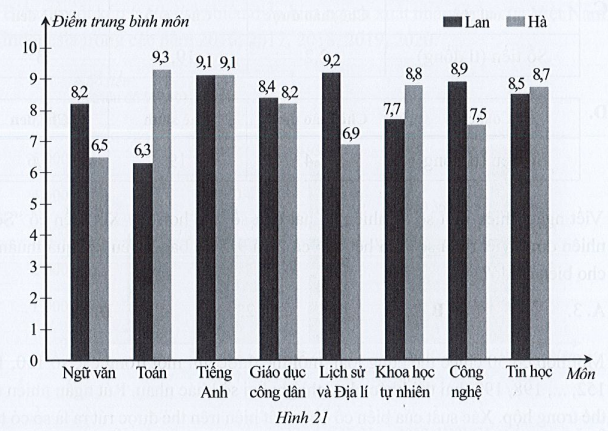
Chênh lệch tổng số điểm trung bình Học kì II các môn trên của hai học sinh Lan và Hà là:
A. 1,5 điểm;
B. 1,1 điểm;
C. 0,8 điểm;
D. 1,3 điểm.
Lời giải:
Đáp án đúng là: D
‒ Nhìn vào cột (màu đậm) của biểu đồ cột kép ở Hình 21 biểu thị kết quả điểm trung bình Học kì II môn Ngữ văn của bạn Lan, ta thấy trên đỉnh cột đó ghi số 8,2 và đơn vị tính ghi trên trục thẳng đứng là điểm trung bình môn. Vậy điểm trung bình môn Ngữ Văn của bạn Lan là 8,2.
Tương tự như trên, ta xác định được điểm trung bình môn Toán, Tiếng Anh, Giáo dục công dân, Lịch sử và Địa lí, Khoa học tự nhiên, Công nghệ, Tin học của bạn Lan lần lượt là: 6,3; 9,1; 8,4; 9,2; 7,7; 8,9; 8,5.
Do đó, tổng điểm trung bình Học kì II các môn của bạn Lan là:
8,2 + 6,3 + 9,1 + 8,4 + 9,2 + 7,7 + 8,9 + 8,5 = 66,3.
‒ Nhìn vào cột (màu nhạt) của biểu đồ cột kép ở Hình 21 biểu thị kết quả điểm trung bình Học kì II môn Ngữ văn của bạn Hà, ta thấy trên đỉnh cột đó ghi số 6,5 và đơn vị tính ghi trên trục thẳng đứng là điểm trung bình môn. Vậy điểm trung bình môn Ngữ Văn của bạn Hà là 6,5.
Tương tự như trên, ta xác định được điểm trung bình môn Toán, Tiếng Anh, Giáo dục công dân, Lịch sử và Địa lí, Khoa học tự nhiên, Công nghệ, Tin học của bạn Hà lần lượt là: 9,3; 9,1; 8,2; 6,9; 8,8; 7,5; 8,7.
Do đó, tổng điểm trung bình Học kì II các môn của bạn Hà là:
6,5 + 9,3 + 9,1 + 8,2 + 6,9 + 8,8 + 7,5 + 8,7 = 65.
Chênh lệch tổng số điểm trung bình Học kì II các môn trên của Lan và Hà là:
66,3 – 65 = 1,3.
Vậy ta chọn phương án D.
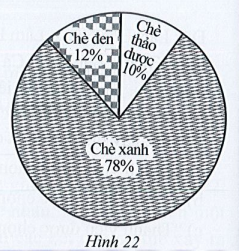
Bảng nào sau đây là bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè năm 2020?
A.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,1 |
3,2 |
B.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
C.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,2 |
19,2 |
3 |
D.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,4 |
19 |
3,6 |
Lời giải:
Đáp án đúng là: B
Dựa vào biểu đồ biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh ta có tỉ số phần trăm các loại là:
• Chè thảo dược: 10%;
• Chè xanh: 78%.
• Chè đen: 12%;
Khi đó, ta có:
• Số tiền công ty chè Phú Minh thu được ở chè thảo dược năm 2020 là:
25 . 10% = 25 . = 2,5 (tỉ đồng).
• Số tiền công ty chè Phú Minh thu được ở chè xanh năm 2020 là:
25 . 78% = 25 . = 19,5 (tỉ đồng).
• Số tiền công ty chè Phú Minh thu được ở chè đen năm 2020 là:
25 . 12% = 25 . = 3 (tỉ đồng).
Vậy ta có bảng số liệu sau:
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
Vậy ta chọn phương án B.
A. 3;
B. 2;
C. 23;
D. 22.
Lời giải:
Đáp án đúng là: A
Tập hợp các kết quả có thể xảy ra đối với số tự nhiên có hai chữ số nhỏ hơn 70 được viết ra là: M = {10, 11, 12,..., 68, 69}.
Trong các số 10, 11, 12,..., 68, 69, có 3 số là số chia hết cho cả 2 và 9 là: 18, 36, 54.
Vậy có 3 kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số chia hết cho cả 2 và 9” là: 18, 36, 54 (lấy ra từ tập hợp M = {10, 11, 12,..., 68, 69}).
Vậy ta chọn phương án A.
A. ;
B. ;
C. ;
D. .
Lời giải:
Đáp án đúng là: D
Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:
M = {150, 151, 152,..., 198, 199}.
Số các phần tử của tập hợp M là 199 – 150 + 1 = 50.
Trong các số 150, 151, 152,..., 198, 199, có 5 số có tổng ba chữ số bằng 12 là: 156, 165, 174, 183, 192.
Vậy có 5 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng ba chữ số bằng 12” là: 156, 165, 174, 183, 192 (lấy ra từ tập hợp M = {150, 151, 152,..., 198, 199}).
Do đó, xác xuất của biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng ba chữ số bằng 12” là: .
Vậy ta chọn phương án D.
Giải SBT Toán 7 trang 27 Tập 2
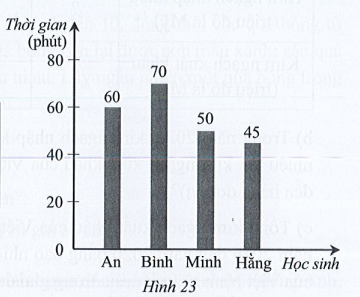
a) Lập bảng số liệu thống kê thời gian luyện tập của bốn học sinh trên theo mẫu sau:
|
Học sinh |
An |
Bình |
Minh |
Hằng |
|
Thời gian (phút) |
? |
? |
? |
? |
b) Tính tỉ số giữa thời gian luyện tập của bạn Bình với tổng thời gian luyện tập của ba bạn An, Minh, Hằng.
c) Thời gian luyện tập của bạn Hằng bằng bao nhiêu phần trăm thời gian luyện tập của bạn An?
Lời giải:
a) Nhìn vào biểu đồ Hình 23 biểu diễn thời gian luyện tập trong ngày của bốn bạn An, Bình, Minh, Hằng, ta thấy trên đỉnh cột tương ứng ghi số 60, 70, 50, 45 và đơn vị tính ghi trên trục thẳng đứng là thời gian (phút). Từ đó ta có bảng số liệu thống kê thời gian luyện tập của bốn học sinh như sau:
|
Học sinh |
An |
Bình |
Minh |
Hằng |
|
Thời gian (phút) |
60 |
70 |
50 |
45 |
b) Thời gian luyện tập của bạn Bình là: 70 phút.
Tổng thời gian luyện tập của ba bạn An, Minh, Hằng là: 60 + 50 + 45 = 155 (phút).
Tỉ số giữa tổng số giữa thời gian luyện tập của bạn Bình với tổng thời gian luyện tập của ba bạn An, Minh, Hằng là: .
Vậy tỉ số giữa thời gian luyện tập của bạn Bình với tổng thời gian luyện tập của ba bạn An, Minh, Hằng bằng
c) Thời gian luyện tập của bạn Hằng là: 45 phút;
Thời gian luyện tập của bạn An là: 60 phút.
Tỉ số phần trăm thời gian luyện tập của bạn Hằng so với thời gian luyện tập của bạn An là:
. 100% = 75%.
Vậy thời gian luyện tập của bạn Hằng bằng 75% thời gian luyện tập của bạn An.
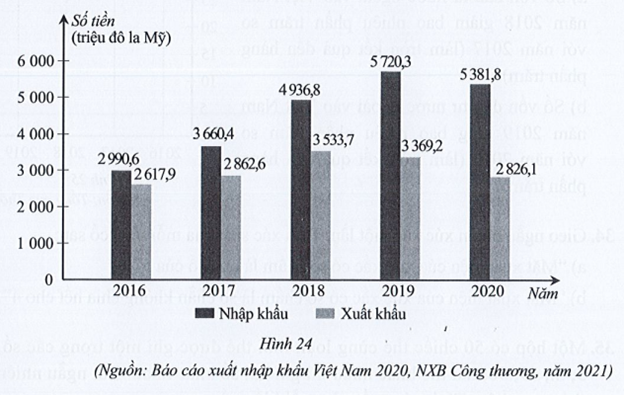
a) Lập bảng số liệu thống kê kim ngạch xuất nhập khẩu của Việt Nam với Indonesia theo mẫu sau:
|
Năm |
2016 |
2017 |
2018 |
2019 |
2020 |
|
Kim ngạch nhập khẩu (triệu đô la Mỹ) |
? |
? |
? |
? |
? |
|
Kim ngạch xuất khẩu (triệu đô la Mỹ) |
? |
? |
? |
? |
? |
b) Trong năm 2020, kim ngạch nhập khẩu của Việt Nam từ Indonesia gấp bao nhiêu lần kim ngạch xuất khẩu của Việt Nam sang Indonesia (làm tròn kết quả đến hàng đơn vị)?
c) Tổng kim ngạch xuất khẩu của Việt Nam sang Indonesia trong giai đoạn từ năm 2016 đến năm 2020 bằng bao nhiêu phần trăm tổng kim ngạch nhập khẩu của Việt Nam từ Indonesia trong giai đoạn từ năm 2016 đến năm 2020 (làm tròn kết quả đến hàng đơn vị)?
Lời giải:
a)
‒ Nhìn vào cột (màu đậm) của biểu đồ cột kép ở Hình 24 biểu thị kim ngạch nhập khẩu của Việt Nam từ Indonesia trong năm 2016, ta thấy trên đỉnh cột đó ghi số 2 990,6 và đơn vị tính ghi trên trục thẳng đứng là triệu đô la Mỹ. Vậy kim ngạch nhập khẩu của Việt Nam từ Indonesia trong năm 2016 là 2 990,6 triệu đô la Mỹ.
Tương tự như trên, ta xác định được kim ngạch nhập khẩu của Việt Nam từ Indonesia trong các năm 2017, 2018, 2019, 2020 lần lượt là: 3 660,4; 4 936,8; 5 720,3; 5 381,8 (triệu đô la Mỹ).
‒ Nhìn vào cột (màu nhạt) của biểu đồ cột kép ở Hình 24 biểu thị kim ngạch xuất khẩu của Việt Nam sang Indonesia trong năm 2016, ta thấy trên đỉnh cột đó ghi số 2 617,9 và đơn vị tính ghi trên trục thẳng đứng là triệu đô la Mỹ. Vậy kim ngạch xuất khẩu của Việt Nam sang Indonesia trong năm 2016 là 2 617,9 triệu đô la Mỹ.
Tương tự như trên, ta xác định được kim ngạch nhập khẩu của Việt Nam sang Indonesia trong các năm 2017, 2018, 2019, 2020 lần lượt là: 2 862,6; 3 533,7; 3 369,2; 2 826,1 (triệu đô la Mỹ).
Ta có bảng số liệu sau:
|
Năm |
2016 |
2017 |
2018 |
2019 |
2020 |
|
Kim ngạch nhập khẩu (triệu đô la Mỹ) |
2 990,6 |
3 660,4 |
4 936,8 |
5 720,3 |
5 381,8 |
|
Kim ngạch xuất khẩu (triệu đô la Mỹ) |
2 617,9 |
2 862,6 |
3 533,7 |
3 369,2 |
2 826,1 |
b) Trong năm 2020, kim ngạch nhập khẩu của Việt Nam từ Indonesia gấp số lần kim ngạch xuất khẩu của Việt Nam sang Indonesia là: ≈ 2 (lần).
Vậy trong năm 2020, kim ngạch nhập khẩu của Việt Nam từ Indonesia gấp khoảng 2 lần kim ngạch xuất khẩu của Việt Nam sang Indonesia.
c) Tổng kim ngạch nhập khẩu của Việt Nam từ Indonesia trong giai đoạn từ năm 2016 đến năm 2020 là:
2 990,6 + 3 660,4 + 4 936,8 + 5 720,3 + 5 381,8 = 22 689,9 (triệu đô la Mỹ).
Tổng kim ngạch xuất khẩu của Việt Nam sang Indonesia trong giai đoạn từ năm 2016 đến năm 2020 là:
2 617,9 + 2 862,6 + 3 533,7 + 3 369,2 + 2 826,1 = 15 209,5 (triệu đô la Mỹ).
Vậy tỉ số phần trăm tổng kim ngạch xuất khẩu của Việt Nam sang Indonesia trong giai đoạn từ năm 2016 đến năm 2020 và tổng kim ngạch nhập khẩu của Việt Nam từ Indonesia trong giai đoạn từ năm 2016 đến năm 2020 là:
. 100% ≈ 67%.
Vậy tổng kim ngạch xuất khẩu của Việt Nam sang Indonesia trong giai đoạn từ năm 2016 đến năm 2020 bằng khoảng 67% tổng kim ngạch nhập khẩu của Việt Nam từ Indonesia trong giai đoạn từ năm 2016 đến năm 2020.
Giải SBT Toán 7 trang 28 Tập 2
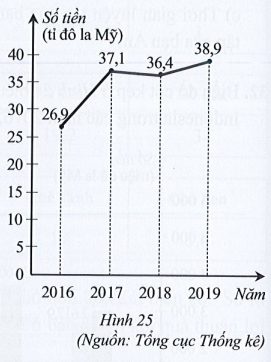
a) Số vốn đầu tư nước ngoài vào Việt Nam năm 2018 giảm bao nhiêu phần trăm so với năm 2017 (làm tròn kết quả đến hàng phần trăm)?
b) Số vốn đầu tư nước ngoài vào Việt Nam năm 2019 tăng bao nhiêu phần trăm so với năm 2016 (làm tròn kết quả đến hàng phần trăm)?
Lời giải:
a) Dựa vào biểu đồ Hình 25 ta có:
Số vốn đầu tư nước ngoài vào Việt Nam năm 2017 là: 37,1 tỉ đô la Mỹ;
Số vốn đầu tư nước ngoài vào Việt Nam năm 2018 là: 36,4 tỉ đô la Mỹ.
Do đó, tỉ số phần trăm số vốn đầu tư nước ngoài vào Việt Nam năm 2018 so với năm 2017 là: . 100% ≈ 98,11%.
Vậy số vốn đầu tư nước ngoài vào Việt Nam năm 2018 giảm 100% ‒ 98,11% = 1,89% so với năm 2017.
b) Dựa vào biểu đồ Hình 25 ta có:
Số vốn đầu tư nước ngoài vào Việt Nam năm 2016 là: 26,9 tỉ đô la Mỹ;
Số vốn đầu tư nước ngoài vào Việt Nam năm 2019 là: 38,9 tỉ đô la Mỹ.
Do đó, tỉ số phần trăm số vốn đầu tư nước ngoài vào Việt Nam năm 2019 so với năm 2016 là: . 100% ≈ 144,61%.
Vậy số vốn đầu tư nước ngoài vào Việt Nam năm 2019 tăng 144,61% - 100% = 44,61% so với năm 2016.
a) “Mặt xuất hiện của xúc xắc có số chấm là ước số của 5”;
b) “Mặt xuất hiện của xúc xắc có số chấm là số chẵn không chia hết cho 4”.
Lời giải:
Tập hợp các kết quả có thể xảy ra đối với xúc xắc là:
A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.
a) Trong các số 1, 2, 3, 4, 5, 6, có hai số là ước của 5 là: 1, 5.
Vậy có 2 kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước số của 5” là: mặt 1 chấm, mặt 5 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước số của 5” là:
b) Trong các số 1, 2, 3, 4, 5, 6, có hai số là số chẵn không chia hết cho 4 là: 2, 6.
Vậy có 2 kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn không chia hết cho 4” là: mặt 2 chấm, mặt 6 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn không chia hết cho 4” là:
a) “Số xuất hiện trên thẻ được rút ra là số lớn hơn 25”;
b) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 3”;
c) “Số xuất hiện trên thẻ được rút ra là số khi chia cho 11 dư 2 và chia cho 5 dư 3”.
Lời giải:
Tập hợp C gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:
C = {1, 2, 3, …, 49, 50}.
Số các phần tử của tập hợp C là 50.
a) Trong các số 1, 2, 3, ..., 49, 50, có 25 số có hai chữ số lớn hơn 25 là: 26, 27, 28, ..., 49, 50.
Vậy có 25 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra lớn hơn 25” là: 26, 27, 28,...,49, 50 (lấy ra từ tập hợp C = {1, 2, 3, …, 49, 50}).
Do đó, xác xuất của biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số lớn hơn 25” là: .
b) Trong các số 1, 2, 3, ..., 49, 50, có 14 số có chứa chữ số 3 là là: 3, 13, 23, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 43.
Vậy có 14 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 3” là: 3, 13, 23, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 43 (lấy ra từ tập hợp C = {1, 2, 3, …, 49, 50}).
Do đó, xác xuất của biến cố “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 3” là: .
c) Trong các số 1, 2, 3, ..., 49, 50, có một số chia cho 11 dư 2 và chia cho 5 dư 3 là: 13.
Vậy có một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 11 dư 2 và chia cho 5 dư 3” là: 13 (lấy ra từ tập hợp C = {1, 2, 3, …, 49, 50}).
Do đó, xác xuất của biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 11 dư 2 và chia cho 5 dư 3” là: .
Giải SBT Toán 7 trang 29 Tập 2
a) “Quả bóng được chọn ra màu vàng”;
b) “Quả bóng được chọn ra màu xanh”;
c) “Quả bóng được chọn ra ghi số chẵn”;
d) “Quả bóng được chọn ra màu vàng và ghi số chẵn”.
Lời giải:
Do các quả bóng có kích thước và khối lượng như nhau nên khả năng được chọn là như nhau nên tập hợp các kết quả có thể xảy ra đối với quả bóng được chọn ra là:
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
a) Trong số các quả bóng được chọn, có 6 quả có màu vàng được đánh số là: 1, 2, 3, 4, 5, 6.
Vậy có 6 kết quả thuận lợi cho biến cố “Quả bóng được chọn ra màu vàng” là: 1, 2, 3, 4, 5, 6 (lấy ra từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}).
Do đó, xác xuất của biến cố “Quả bóng được chọn ra màu vàng” là: .
b) Do có tất cả 10 quả bóng, 6 quả bóng màu vàng đánh số: 1, 2, 3, 4, 5, 6 nên còn lại có 4 quả màu xanh đánh số: 7, 8, 9, 10.
Vậy có 4 kết quả thuận lợi cho biến cố “Quả bóng được chọn ra màu xanh” là: 7, 8, 9, 10 (lấy ra từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}).
Do đó, xác xuất của biến cố “Quả bóng được chọn ra màu xanh” là: .
c) Trong số các quả bóng được chọn, có 5 quả được đánh số chẵn là: 2, 4, 6, 8, 10.
Vậy có 5 kết quả thuận lợi cho biến cố “Quả bóng được chọn ra ghi số chẵn” là: 2, 4, 6, 8, 10, (lấy ra từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}).
Do đó, xác xuất của biến cố “Quả bóng được chọn ra ghi số chẵn” là: .
d) Trong số các quả bóng được chọn, có 3 quả màu vàng ghi số chẵn là: 2, 4, 6.
Vậy có 3 kết quả thuận lợi cho biến cố “Quả bóng được chọn ra màu vàng và ghi số chẵn” là: 2, 4, 6 (lấy ra từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}).
Do đó, xác xuất của biến cố “Quả bóng được chọn ra màu vàng và ghi số chẵn” là:
a) “Học sinh được chọn học tiếng Anh”;
b) “Học sinh được chọn học tiếng Pháp”;
c) “Học sinh được chọn học cả tiếng Anh và tiếng Pháp”.
Lời giải:
a) Có 40 học sinh học tiếng Anh trong tổng số 60 học sinh.
Do đó, xác suất của các biến cố “Học sinh được chọn học tiếng Anh” là: .
b) Có 30 học sinh học tiếng Anh trong tổng số 60 học sinh
Do đó, xác suất của các biến cố “Học sinh được chọn học tiếng Pháp” là: .
c) Có 20 học sinh học cả tiếng Anh và tiếng Pháp trong tổng số 60 học sinh
Do đó, xác suất của các biến cố “Học sinh được chọn học cả tiếng Anh và tiếng Pháp” là: .
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
SBT Toán 7 Bài 6 : Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
SBT Toán 7 Bài tập cuối chương 5
SBT Toán 7 Bài 1 : Biểu thức số. Biểu thức đại số
SBT Toán 7 Bài 2 : Đa thức một biến. Nghiệm của đa thức một biến
SBT Toán 7 Bài 3 : Phép cộng, phép trừ đa thức một biến
Lý thuyết Toán 7 Chương 5: Một số yếu tố thống kê và xác suất
1. Thu thập và phân loại dữ liệu
Trong các dữ liệu thống kê thu thập được, có những dữ liệu thống kê là số (số liệu) nhưng cũng có những dữ liệu thống kê không phải là số.
2. Tính hợp lí của dữ liệu
Sau khi thu thập, tổ chức, phân loại dữ liệu, ta cần xem xét tính hợp lí của những dữ liệu thống kê đó, đặc biệt chỉ ra được những dữ liệu không hợp lí. Ta có thể dựa trên những tiêu chí toán học đơn giản để thực hiện điều đó.
3. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
Ở lớp 6, chúng ta đã làm quen với việc mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ (bảng số liệu, biểu đồ tranh, biểu đồ cột, biểu đồ cột kép).
Ở lớp 7, chúng ta tiếp tục tìm hiểu sâu hơn việc đọc hiểu, rút ra những thông tin cần thiết từ những dạng biểu diễn dữ liệu đã học và nhận biết những dạng biểu diễn khác nhau cho một tập dữ liệu.
4. Phân tích và xử lí dữ liệu để rút ra kết luận
Sau khi thu thập, tổ chức, phân loại, biểu diễn dữ liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận. Thông thường, quá trình phân tích và xử lí dữ liệu dựa trên tính toán và suy luận toán học.
5. Tính hợp lí của kết luận thống kê
Quá trình phân tích và xử lí dữ liệu giúp chúng ta có thể nhận biết được: tính hợp lí của dữ liệu thống kê, tính hợp lí của kết luận thống kê và ta cũng có thể bác bỏ kết luận đã nêu ra. Thông thường, để làm được điều đó ta dựa trên những tiêu chí đơn giản hoặc dựa trên tính toán và suy luận toán học.
6. Biểu đồ đoạn thẳng
Biểu đồ đoạn thẳng có các yếu tố sau:
+ Trục nằm ngang biểu diễn các đối tượng thống kê;
+ Trục thẳng đứng biểu diễn tiêu chí thống kê và trên trục đó đã xác định độ dài đơn vị thống kê;
+ Biểu đồ đoạn thẳng là đường gấp khúc nối từng điểm liên tiếp bằng các đoạn thẳng;
+ Mỗi điểm đầu mút của các đoạn thẳng trong đường gấp khúc được xác định bởi một đối tượng thống kê và số liệu thống kê theo tiêu chí của đối tượng đó.
Chú ý:
+ Cũng như biểu đồ cột và biểu đồ cột kép, biểu đồ đoạn thẳng giúp chúng ta “trực quan hóa” một tập dữ liệu thống kê thông qua cách biểu diễn hình học tập dữ liệu đó.
+ Người ta còn biểu diễn dữ liệu thống kê ở dạng biểu đồ tương tự biểu đồ cột, trong đó các cột được thay bằng các đoạn thẳng. Biểu đồ đó cũng gọi là biểu đồ đoạn thẳng.
Nhận xét: Như ta đã biết, dữ liệu thống kê có thể biểu diễn ở những dạng khác nhau, trong đó có biểu đồ đoạn thẳng.
7. Phân tích và xử lí dữ liệu biểu diễn bằng biểu đồ đoạn thẳng
Dựa vào biểu đồ đoạn thẳng, ta có thể xác định xu hướng tăng hoặc giảm của tập số liệu trong một khoảng thời gian nhất định.
8. Biểu đồ hình quạt tròn
Biểu đồ hình quạt tròn có các yếu tố sau:
+ Đối tượng thống kê được biểu diễn bằng các hình quạt tròn.
+ Số liệu thống kê theo tiêu chí thống kê của mỗi đối tượng (thống kê) được ghi ở hình quạt tròn tương ứng. Số liệu thống kê đó được tính theo tỉ số phần trăm.
+ Tổng các tỉ số phần trăm ghi ở các hình quạt tròn là 100%, nghĩa là tổng các tỉ số phần trăm của các số liệu thành phần phải bằng 100% (của tổng thể thống kê).
Nhận xét:
Thông thường, trong bảng số liệu, ta có thể nhận biết nhanh chóng số liệu thống kê (theo tiêu chí) của mỗi đối tượng thống kê nhưng không biết được mỗi đối tượng đó chiếm bao nhiêu phần trăm trong tổng thể thống kê.
Ngược lại, trong biểu đồ hình quạt tròn, ta có thể nhận biết nhanh chóng mỗi đối tượng thống kê chiếm bao nhiêu phần trăm trong tổng thể thống kê nhưng lại không biết được số liệu thống kê (theo tiêu chí) của mỗi đối tượng đó.
Vì thế, tùy theo mục đích thống kê, ta sẽ lựa chọn bảng số liệu hay biểu đồ hình quạt trong để biểu diễn dữ liệu thống kê.
9. Phân tích và xử lí dữ liệu biểu diễn bằng biểu đồ hình quạt tròn
Dựa trên việc biểu diễn dữ liệu bằng biểu đồ hình quạt tròn, ta có thể phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận.
10. Biến cố trong trò chơi gieo xúc xắc
Trong trò chơi gieo xúc xắc, ta quy ước xúc xắc là cân đối và đồng chất.
Mỗi xúc xắc có sáu mặt, số chấm ở mỗi mặt là một trong các số 1; 2; 3; 4; 5; 6. Gieo ngẫu nhiên xúc xắc một lần.
Nhận xét:
+ Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:
A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.
+ Tập hợp các kết quả có thể xảy ra đối với sự kiện “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” là: B = {mặt 2 chấm; mặt 4 chấm; mặt 6 chấm} (gồm ba phần tử lấy ra từ tập hợp A).
+ Trong trò chơi gieo xúc xắc, sự kiện “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” còn gọi là biến cố, hay gọi đầy đủ là biến cố ngẫu nhiên. Sở dĩ ta có thêm cụm từ “ngẫu nhiên” là vì các kết quả xảy ra có tính ngẫu nhiên, ta không thể đoán trước được.
+ Mỗi kết quả: mặt 2 chấm, mặt 4 chấm, mặt 6 chấm (là phần tử của tập hợp B), được gọi là một kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn”. Sở dĩ ta gọi những kết quả đó là thuận lợi cho biến cố trên vì chúng đáp ứng được mong muốn thể hiện trong biến cố, đó là mặt xuất hiện có số chấm là số chẵn.
11. Biến cố trong trò chơi rút thẻ từ trong hộp
Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.
Nhận xét:
+ Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:
C = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}.
+ Tập hợp các kết quả có thể xảy ra đối với sự kiện “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4” là: D = {4; 8; 12} (gồm ba phần tử lấy ra từ tâp hợp C).
+ Trong trò chơi rút thẻ từ trong hộp, sự kiện “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4” cũng gọi là biến cố (hay gọi đầy đủ là biến cố ngẫu nhiên).
+ Mỗi kết quả: 4; 8; 12 (là phần tử của tập hợp D), được gọi là một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
12. Xác suất của biến cố trong trò chơi gieo xúc xắc
Trong trò chơi gieo ngẫu nhiên xúc xắc một lần:
Xác suất của một biến cố trong trò chơi gieo xúc xắc bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.
Ví dụ: Gieo ngẫu nhiên xúc xắc một lần.
a) Tìm số phần tử của tập hợp E gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.
b) Xét biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3”. Tính xác suất của biến cố đó.
Hướng dẫn giải
a) Tập hợp gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:
E = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.
Vậy số phần tử của tập hợp E là 6.
b) Trong các số 1; 2; 3; 4; 5; 6, các số không chia hết cho 3 là: 1; 2; 4; 5.
Do đó có bốn kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3” là mặt 1 chấm; mặt 2 chấm; mặt 4 chấm; mặt 5 chấm.
Xác suất của biến cố đó là .
Vậy xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3” là .
Chú ý: Trong trò chơi gieo xúc xắc trên, số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là 6. Nếu k là số các kết quả thuận lợi cho biến cố thì xác suất của biến cố đó bằng .
13. Xác suất của biến cố trong trò chơi rút thẻ từ trong hộp
Trong trò chơi rút thẻ từ trong hộp:
Xác suất của một biến cố trong trò chơi rút thẻ từ trong hộp bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
Ví dụ: Một hộp gồm 15 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; ...; 14; 15. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.
a) Tìm số phần tử của tập hợp F gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
b) Xét biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1”. Tính xác suất của biến cố đó.
Hướng dẫn giải
a) Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:
F = {1; 2; 3; 4; ...; 14; 15}.
Vậy số phần tử của tập hợp F là 15.
b) Trong các số 1; 2; 3; 4; ...; 14; 15, các số chia 5 dư 1 là 1; 6; 11.
Do đó có ba kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1” là 1; 6; 11.
Xác suất của biến cố đó là .
Vậy xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1” là .