Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt hay, chi tiết giúp học sinh dễ dàng làm bài tập Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt lớp 9.

Giải bài tập Toán lớp 9 Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 114 SGK Toán lớp 9 Tập 2: Chiếc nón (h. 88) có dạng mặt xung quanh là một hình nón. Cho biết, đâu là đường tròn đáy, đâu là mặt xung quanh, đâu là đường sinh của nón.

Lời giải:

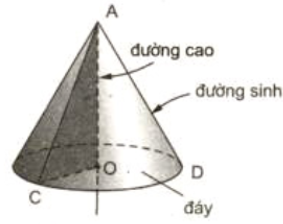
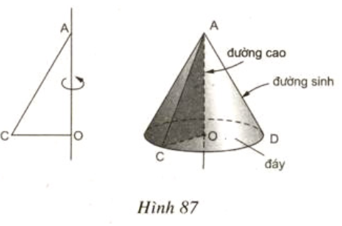
Đường tròn đáy là phần vành rộng nhất của nón

Mặt xung quanh là phần bên ngoài của nón, tính từ đỉnh nón đến đường tròn đáy

Đường sinh là đường thẳng bất kì, nối từ đỉnh đến đường tròn đáy.

Bài 15 trang 117 SGK Toán lớp 9 Tập 2: Một hình nón được đặt vào bên trong một hình lập phương như hình vẽ (cạnh của hình lập phương bằng 1) (h.93). Hãy tính:

a) Bán kính đáy của hình nón.

b) Độ dài đường sinh.

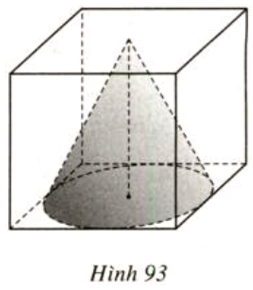
Lời giải:

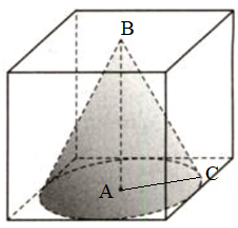
a)

Có đường tròn đáy của hình nón nội tiếp trong hình vuông có cạnh là 1 là một mặt của hình lập phương. Do đó bán kính của đáy hình nón bằng một nửa cạnh hình lập phương và bằng r = 0,5

b)

Đỉnh của hình nón tiếp xúc với một mặt của hình lập phương nên đường cao của hình nón bằng với cạnh của hình lập phương hay chiều cao h = 1

Với l là độ dài đường sinh của hình nón.

Xét tam giác ABC vuông tại A có:

BC = l

AC = r

AB = h

Áp dụng định lý Py-ta-go ta có:

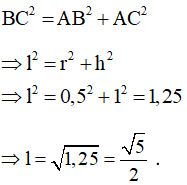
Bài tập (trang 117; 118)

Bài 16 trang 117 SGK Toán lớp 9 Tập 2: Cắt mặt cắt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết bán kính hình quạt tròn bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.

Quan sát hình 94 và tính số đo cung của hình quạt tròn.

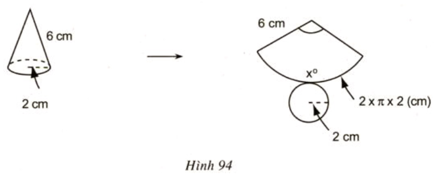
Lời giải:

Ta thấy hình nón có bán kính đáy r = 2cm. Suy ra chu vi đáy của hình nón là:

$C=2\pi r=2\pi .2=4\pi$ (cm)

Lại thấy hình quạt có bán kính R = 6cm và độ dài cung là l = C = $4\mathrm{\pi }$ (cm)

Gọi $x^0$ (x > 0) là số đo của cung hình quạt

Khi đó, độ dài cung là:

$$\begin{gathered} l=\frac{\pi Rx}{180} \\ \Rightarrow x=\frac{180.l}{\pi R}=\frac{180.4\pi }{\pi .6}=120 \end{gathered}$$

Vậy số đo cung của hình quạt tròn là ${120}^0$.

Bài 17 trang 117 SGK Toán lớp 9 Tập 2: Khi quay tam giác vuông để tạo ra một hình nón như hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là , độ dài đường sinh là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.

Lời giải:

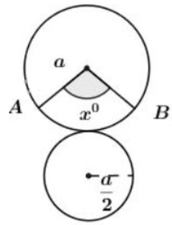
Theo đề bài ta có: $\widehat{CAO}={30}^o$ nên góc ở đỉnh của hình nón là $\widehat{CAB}={60}^o$, suy ra đường kính của đường tròn đáy của hình nón bằng a (do tam giác ABC đều).

Vậy bán kính đáy của hình nón là: $\frac{a}{2}$

Chu vi đáy hình nón là: $C=2\pi .\frac{a}{2}=\pi a$

Đường sinh của hình nón là AC = a (do tam giác ABC đều)

Khai triển mặt xung quanh hình nón ta được hình quạt AOB có bán kính R = a

Gọi số đo cung AB là $x^0$, độ dài cung AB là:  $l=\frac{\pi ax}{180}$

Mặt khác, độ dài cung AB bằng chu vi đáy hình nón nên ta có:

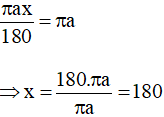
Vậy  số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón là ${180}^0$.

Bài 18 trang 117 SGK Toán lớp 9 Tập 2: Hình ABCD (h.95) khi quay quanh BC thì tạo ra:

(A) Một hình trụ

(B) Một hình nón

(C) Một hình nón cụt

(D) Hai hình nón

(E) Hai hình trụ

Hãy chọn câu trả lời đúng.

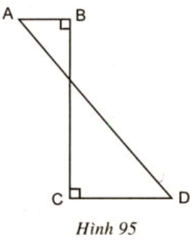
Lời giải:

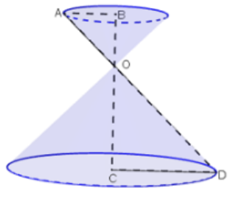
Gọi O là giao điểm của BC và AD

Khi quay hình ABCD quanh BC có nghĩa là tam giác vuông OBA quanh OB và tam giác vuông OCD quanh OC

Mỗi hình tam giác vuông trên quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ tạo ra 2 hình nón.

Vậy ta chọn đáp án (D).

Bài 19 trang 118 SGK Toán lớp 9 Tập 2: Hình khai triển của mặt xung quanh của một hình nón là một hình quạt. Nếu bán kính hình quạt là 16cm, số đo cung là ${120}^0$ thì độ dài đường sinh của hình nón là:

(A) 16 cm                                         

(B) 8 cm                                  

(C) $\frac{16}{3}$ cm

(D) 4 cm                                           

(E) $\frac{16}{5}$ cm

Hãy chọn kết quả đúng.

Lời giải:

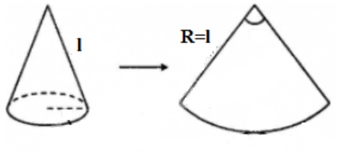
Khi khai triển mặt xung quanh hình nón thì ta được hình quạt có bán kính bằng đường sinh của hình nón.

Đầu bài cho bán kính hình tròn chứa hình quạt là 16cm nên độ dài đường sinh là 16cm

Vậy ta chọn đáp án (A).

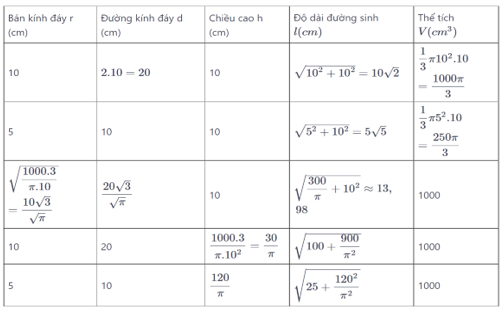
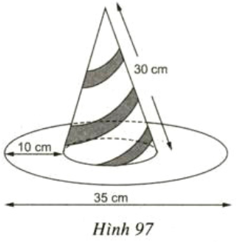
Bài 20 trang 118 SGK Toán lớp 9 Tập 2: Hãy điền đủ vào các ô trống ở bảng sau (xem hình 96):

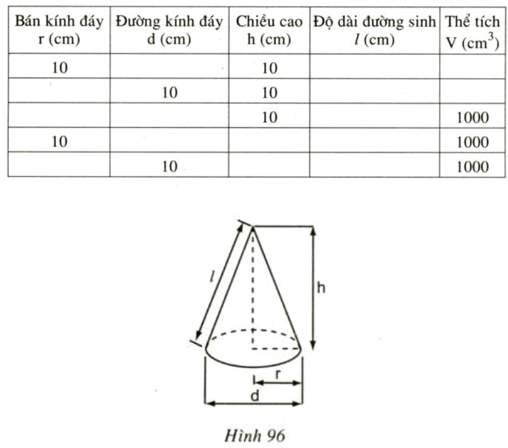
Lời giải:

Áp dụng các công thức:

Cho hình nón có bán kính đáy là r và đường sinh l

Ta có:

Bài 21 trang 118 SGK Toán lớp 9 Tập 2: Cái mũ của chú hề với các kích thước cho theo hình vẽ (h.97). Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa).

Lời giải:

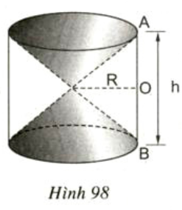
Diện tích vải cần dùng bằng tổng diện tích xung quanh hình nón và diện tích hình vành khăn.

Gọi S là diện tích vải cần có, $S_{xq}$ là diện tích xung quanh của hình nón, $S_{vk}$ là diện tích hình vành khăn thì $S=S_{xq}+S_{vk}$

Hình nón có đường sinh l = 30cm và bán kính đáy r = 7,5cm nên diện tích xung quanh của hình nón là:

$$\begin{gathered} S_{xq}=\pi rl=\pi .7,5.30 \\ \approx 706,9\left(c{m}^2\right) \end{gathered}$$

Vậy diện tích vải cần làm mũ là: 

$$\begin{gathered} S=S_{vk}+S_{xq} \\ =785+706,9=1491,9\left(c{m}^2\right) \end{gathered}$$

Bài 22 trang 118 SGK Toán lớp 9 Tập 2: Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (AO = OB). Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.

Lời giải:

Ta có: Hai hình nón bằng nhau do OA = OB, hai đáy bằng nhau cùng bằng đáy của hình trụ

Chiều cao của 1 hình nón là: $OA=OB=\frac{h}{2}$

Chiều cao của hình trụ là: AB = h

Thể tích của mỗi hình nón là:

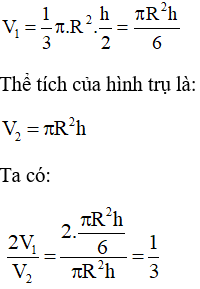
Luyện tập trang 119, 120

Bài 23 trang 119 SGK Toán lớp 9 Tập 2: Viết công thức tính nửa góc ở đỉnh của một hình nón (góc $\alpha$ của tam giác vuông OAS – hình 99) sao cho diện tích mặt khai triển của mặt nón bằng một một phần tư diện tích của hình tròn (bán kính SA).

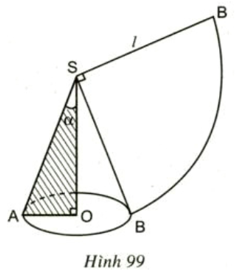
Lời giải:

Xét tam giác SAO vuông tại O có:

Bài 24 trang 119 SGK Toán lớp 9 Tập 2: Hình khai triển của mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là 16cm, số đo cung là ${120}^0$. Tan của nửa góc ở đỉnh của hình nón là:

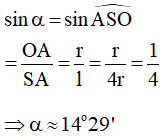
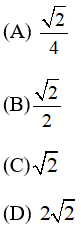
Lời giải:

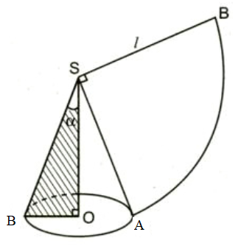
Đường sinh của hình nón là l  = 16

Gọi r là bán kính đáy của hình nón.

Độ dài cung AB của đường tròn chứa hình quạt là:  $\frac{\pi \mathrm{.16.120}}{180}=\frac{32.\pi }{3}$

Và độ dài này bằng chu vi đáy hình nón là:

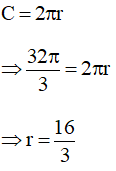
Xét tam giác BOS vuông tại O

Áp dụng định lí Py-ta-go ta có:

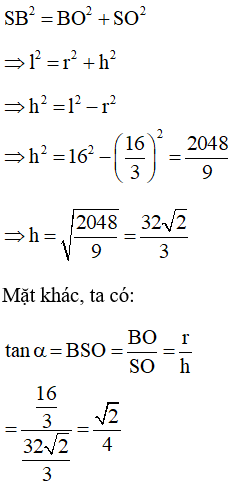
Vậy ta chọn đáp án (A)

Bài 25 trang 119 SGK Toán lớp 9 Tập 2: Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là a,b (a < b) và độ dài đường sinh là l (a, b, l có cùng đơn vị đo).

Lời giải:

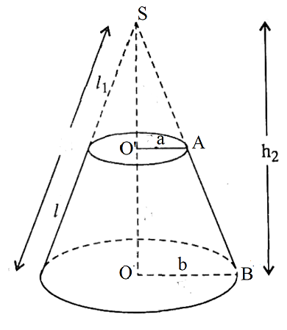
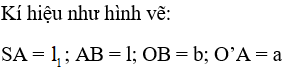
Vì O’A // OB nên ta có tam giác SO’A đồng dạng với tam giác SOB (theo định lí Ta-lét)

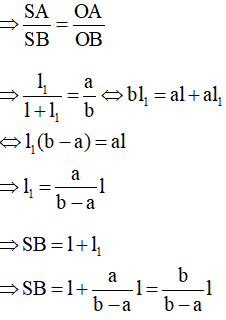
Diện tích xung quanh hình nón lớn là:

 $$\begin{gathered} S_1=\pi .b.SB \\ =\pi .b.\frac{b}{b-a}l=\frac{b^2}{b-a}\pi l \end{gathered}$$

Diện tích xung quanh hình nón nhỏ là:

$$\begin{gathered} S_2=\pi .a.SA \\ =\pi .a.\frac{a}{b-a}l=\frac{a^2}{b-a}\pi l \end{gathered}$$

Diện tích xung quanh hình nón cụt là:

$$\begin{gathered} S=S_1-S_2 \\ =\frac{b^2}{b-a}\pi l-\frac{a^2}{b-a}\pi l \\ =\pi l\left(\frac{b^2}{b-a}-\frac{a^2}{b-a}\right) \\ =\pi l\left[\frac{(b-a)(b+a)}{b-a}\right] \\ =(a+b)\pi l \end{gathered}$$

Vậy diện tích xung quanh nón cụt là: $S=(a+b)\pi l$.

Bài 26 trang 119 SGK Toán lớp 9 Tập 2: Hãy điền đầy đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm):

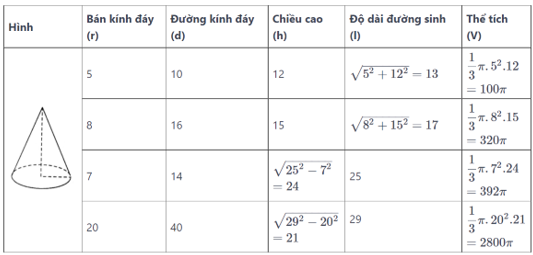
Lời giải:

Áp dụng các công thức:

Cho hình nón có bán kính đáy r, chiều cao h, độ dài đường sinh l

Ta có:

Đường kính đáy: d = 2r

Liên hệ giữa chiều cao, bán kính đáy và đường sinh: $l^2=h^2+r^2$

Thể tích hình nón: $V=\frac{1}{3}\pi r^{2}h$

Bài 27 trang 119 SGK Toán lớp 9 Tập 2: Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình 100. Hãy tính:

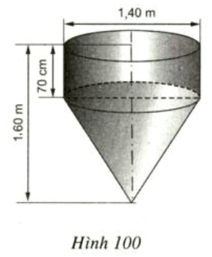
a) Thể tích của dụng cụ này.

b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy).

Lời giải:

a)

Thể tích cần tính gồm một hình trụ có đường kính đáy 1,4m nên bán kính đáy là R = 0,7m, chiều cao h = 70cm = 0,7m; một hình nón có bán kính đáy bằng bán kính hình trụ là r = 0,7m, chiều cao hình nón là h’ = 0,9m.

Thể tích của hình trụ là:

$$\begin{gathered} V_t=\pi R^{2}h=\pi 0,7^2.0,7 \\ \approx 1,077\left(m^3\right) \end{gathered}$$

Thể tích hình nón là:

$$\begin{gathered} V_n=\frac{1}{3}\pi r^{2}h\text{'} \\ =\frac{1}{3}\pi .0,7^2.0,9\approx 0,462\left(m^3\right) \end{gathered}$$

b)

Diện tích cần tính gồm diện tích xung quanh hình trụ và diện tích xung quanh hình nón. Đường sinh của hình nón là:

$$\begin{gathered} l^2=h{\text{'}}^2+r^2 \\ \Rightarrow l=\sqrt{h{\text{'}}^2+r^2} \\ \Rightarrow l=\sqrt{0,9^2+0,7^2}\approx 1,14 \end{gathered}$$

Diện tích xung quanh của hình trụ là:

$$\begin{gathered} S_{xqt}=2\pi Rh=2\pi Rh \\ =2\pi .0,7.0,7\approx 3,077\left(m^2\right) \end{gathered}$$

Diện tích xung quanh của hình nón là:

$$\begin{gathered} S_{xqn}=\pi rl \\ =\pi .0,7.1,4\approx 2,506\left(m^2\right) \end{gathered}$$

Vậy diện tích toàn phần của phễu là:

$$\begin{gathered} S=S_{xqt}+S_{xqn} \\ =3,077+2,506 \\ =5,583\left(m^2\right) \end{gathered}$$

Bài 28 trang 120 SGK Toán lớp 9 Tập 2: Một cái xô bằng inox có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 101 (đơn vị: cm).

a) Hãy tính diện tích xung quanh của xô.

b) Khi xô chứa đầu hóa chất thì dung tích của nó là bao nhiêu ?

Lời giải:

Gọi l là đường sinh của hình nón lớn

Theo định lí Ta-lét ta có:

$$\begin{gathered} \frac{l}{l-36}=\frac{21}{9} \\ \Rightarrow 9l=21(l-36)\Rightarrow l=63 \end{gathered}$$

a)

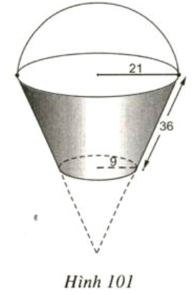
Diện tích cần tính gồm diện tích xung quanh của hình xung quanh của hình nón cụt và diện tích hình tròn đáy có bán kính r = 9cm

Đường sinh của hình nón lớn là l = 63cm

Đường sinh của hình nón nhỏ là: l’ = 63 - 36 = 27 (cm)

Bán kính đáy của hình nón lớn là: R = 21cm

Diện tích xung quanh của hình nón lớn là:

$$\begin{gathered} S_{xq1}=\pi Rl=\pi \mathrm{.21.63} \\ \approx 4154,22\left(c{m}^2\right) \end{gathered}$$

Diện tích xung quanh của hình nón nhỏ là:

$$\begin{gathered} S_{xq2}=\pi .r.l\text{'} \\ =\pi \mathrm{.9.27}\approx 763,02\left(c{m}^2\right) \end{gathered}$$

Diện tích xung quanh của xô chính là diện tích xung quanh của hình nón cụt:

$$\begin{gathered} S_{xqnc}=S_{xq1}-S_{xq2} \\ =4154,22-763,02 \\ =3391,2\left(c{m}^2\right) \end{gathered}$$

b)

Chiều cao của hình nón lớn là h, ta có: 

$$\begin{gathered} R^2+h^2=l^2 \\ \Rightarrow h^2=l^2-R^2 \\ \Rightarrow h=\sqrt{l^2-R^2}=\sqrt{{63}^2-{21}^2} \\ \approx 59,397 \left(cm\right) \end{gathered}$$

Chiều cao của hình nón nhỏ là h’, ta có:

$$\begin{gathered} r^2+h{\text{'}}^2=l{\text{'}}^2 \\ \Rightarrow h{\text{'}}^2=l{\text{'}}^2-r^2 \\ \Rightarrow h\text{'}=\sqrt{l{\text{'}}^2-r^2} \\ =\sqrt{{27}^2-9^2}\approx 25,546 \end{gathered}$$

Thể tích của hình nón lớn là:

$$\begin{gathered} V=\frac{1}{3}\pi R^{2}h \\ =\frac{1}{3}\pi {.21}^2.59,397 \\ \approx 27416,467\left(c{m}^3\right) \end{gathered}$$

Thể tích của hình nón nhỏ là:

$$\begin{gathered} V\text{'}=\frac{1}{3}\pi r^{2}h\text{'} \\ =\frac{1}{3}\pi {.9}^2.25,456 \\ \approx 2158,160\left(c{m}^3\right) \end{gathered}$$

Khi xô chứa đầy hóa chất thì dung tích của nó là thể tích của hình nón cụt là:

$$\begin{gathered} V=V-V\text{'} \\ =27416,467-2158,160 \\ =25258,307\left(c{m}^3\right) \end{gathered}$$

Bài 29 trang 120 SGK Toán lớp 9 Tập 2: Cối xay gió của Đôn-ki-hô-tê từ tác phẩm của Xéc-van-téc (Cervantès).

Phần trên của cối xay gió có dạng một hình nón (h.102). Chiều cao của hình nón là 42cm và thể tích của nó là 17600$c{m}^3$. Em hãy giúp chàng Đôn-ki-hô-tê tính bán kính đáy của hình nón (làm tròn kết quả đên chữ số thập phân thứ hai).

Lời giải:

Theo đề bài ta có:

Thể tích của hình nón là: $V=17600c{m}^3$

Chiều cao của nón là: 42cm

Ta có: $V=\frac{1}{3}\pi R^{2}h$ (với R là bán kính của hình tròn đáy)

$$\begin{gathered} \Rightarrow R=\sqrt{\frac{3V}{\pi h}} \\ =\sqrt{\frac{3.17600}{\pi .42}}\approx 20,00 \left(cm\right) \end{gathered}$$

Vậy bán kính của hình tròn là R = 20,00 cm.