Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung hay, chi tiết giúp học sinh dễ dàng làm bài tập Góc tạo bởi tia tiếp tuyến và dây cung lớp 9.
Giải bài tập Toán lớp 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
Trả lời câu hỏi giữa bài
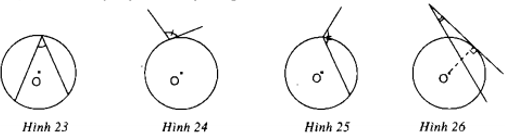
Lời giải:
Các hình trên không phải là góc tạo bởi tiếp tuyến và dây cung vì:
Hình 23: Không có tia nào là tiếp tuyến của đường tròn
Hình 24: Không có tia nào là dây cung của đường tròn
Hình 25: Một tia không là tiếp tuyến của đường tròn
Hình 26: Đỉnh của góc không nằm trên đường tròn.
b) Trong mỗi trường hợp ở câu a), hãy cho biết số đo của cung bị chắn.
Lời giải:
a)
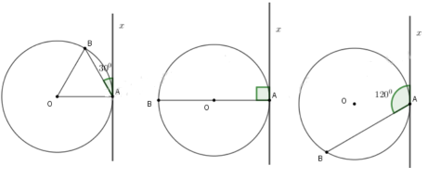
b)
TH1:
Cung bị chắn là cung nhỏ AB
Do Ax là tiếp tuyến của đường tròn (O) nên ta có:
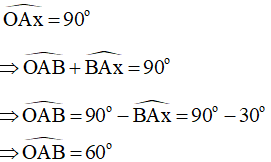
Xét tam giác OAB có:
OA = OB (cùng bằng bán kính đường tròn (O))
Do đó, tam giác OAB cân tại O
Lại có:
Do đó, tam giác OAB là tam giác đều
(tính chất tam giác đều)
Mà góc BOA là góc ở tâm chắn cung nhỏ AB
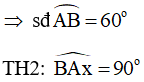
O, A, B thẳng hàng
Do đó, AB là đường kính
Vậy cung bị chắn là nửa đường tròn có số đo là
TH3:
Cung bị chắn là cung lớn AB
Do Ax là tiếp tuyến của đường tròn (O) nên ta có:
Xét tam giác OAB có:
OA = OB (cùng bằng bán kính đường tròn (O))
Do đó, tam giác OAB cân tại O
(tính chất tam giác cân)
Mà:
Mà góc BOA là góc ở tâm chắn cung nhỏ AB
Do đó, số đo cung lớn AB là:
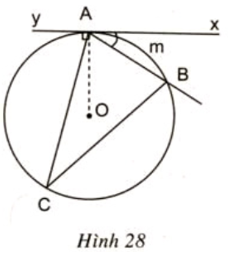
Câu hỏi 3 trang 79 SGK Toán lớp 9 Tập 2: Hãy so sánh số đo của với số đo của cung AmB (h.28).
Lời giải:
Xét đường tròn (O) có:
Góc BAx là góc tạo bởi tiếp tuyến và dây cung AB chắn cung AmB
sđ (1)
Góc BCA là góc nội tiếp đường tròn chắn cung AmB
(2)
Từ (1) và (2) ta suy ra:
Bài tập (trang 79)
Lời giải:
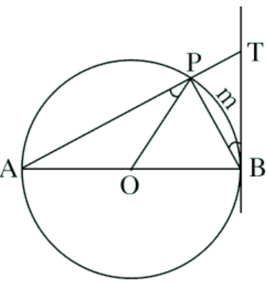
Xét đường tròn (O)
Có:
BT là tiếp tuyến của đường tròn (O) tại P
PB là dây cung
là góc tạo bởi tiếp tuyến và dây cung
sđ (1)
Mặt khác ta có: Góc PAO là góc nội tiếp đường tròn chắn cung PmB
sđ (2)
Từ (1) và (2) ta suy ra: (3)
Xét tam giác OAP có:
OA = OP (cùng bằng bán kính đường tròn tâm O)
Do đó, tam giác OAP cân tại O
(4) (tính chất tam giác cân)
Từ (3) và (4) ta suy ra: (đcpcm).
Lời giải:
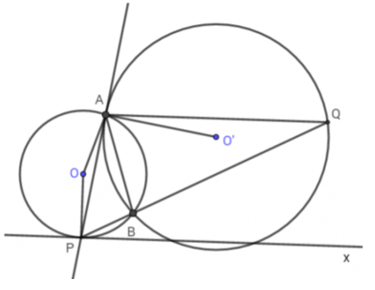
Nối A với B
Ta có:
Góc AQP là góc nội tiếp chắn cung nhỏ AB của đường tròn (O’)
(1)
Góc PAB là góc tạo bởi tiếp tuyến PA và dây cung AB chắn cung nhỏ AB của đường tròn (O’)
(2)
Từ (1) và (2) ta suy ra: (3)
Mặt khác, ta lại có:
Góc PAB là góc nội tiếp chắn cung nhỏ PB của đường tròn (O)
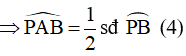
Góc BPx là góc tạo bởi tiếp tuyến Px và dây cung PB chắn cung nhỏ PB của đường tròn (O)
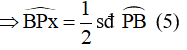
Từ (4) và (5) ta suy ra: (6)
Từ (3) và (6) ta suy ra:
Mà góc AQP và góc BPx là hai góc so le trong
AQ // Px.
Lời giải:
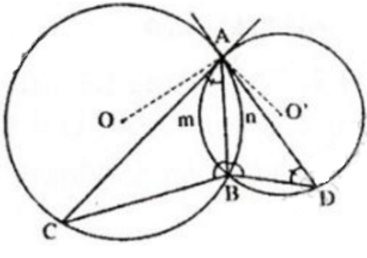
Xét đường tròn (O’) có:
Góc CAB là góc tạo bởi tia tiếp tuyến CA và dây cung AB chắn cung AmB của đường tròn (O’)
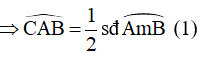
Góc ADB là góc nội tiếp chắn cung AmB của đường tròn (O’)
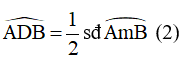
Từ (1) và (2) ta suy ra:
Xét đường tròn (O) có:
Góc ACB là góc nội tiếp đường tròn chắn cung AnB của đường tròn (O)
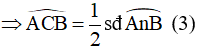
Góc ADB là góc tạo bởi tiếp tuyến AD và dây cung AB chắn cung AnB của đường tròn (O)
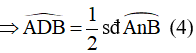
Từ (3) và (4) ta suy ra:
Xét tam giác CBA và tam giác ABD có:
(chứng minh trên)
(chứng minh trên)
Do đó, tam giác CBA đồng dạng với tam giác ABD (góc – góc)
(đcpcm).
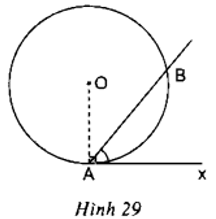
Nếu góc (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB) có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn (h.29).
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.
Lời giải:
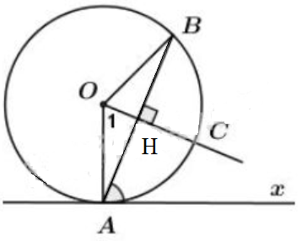
Kẻ OH vuông góc với AB tại H và cắt (O) tại C
Do đó, H là trung điểm của AB và C là điểm chính giữa của cung AB
Theo giả thiết ta có:
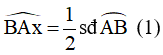
Góc là góc ở tâm chắn cung nhỏ AC nên ta có:
![]()
Mà C là điểm chính giữa của cung AB nên ta có:
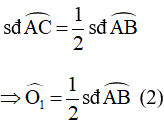
Từ (1) và (2) ta suy ra:
Xét tam giác OHA vuông tại H
Ta có:
Mà: (chứng minh trên)
Do đó, Ax là tiếp tuyến của (O) tại A.
Luyện tập trang 79, 80
Lời giải:
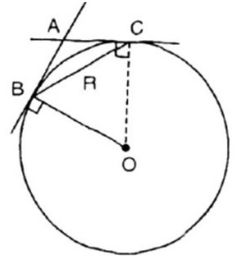
Xét tam giác OBC có:
OB = OC = BC = R
Do đó, tam giác OBC là tam giác đều
Mà góc BOC là góc ở tâm chắn cung nhỏ BC của đường tròn (O)
![]()
Ta có: là góc tạo bởi tia tiếp tuyến BA và dây cung BC chắn cung nhỏ BC
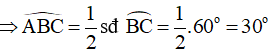
(định lý về góc tạo bởi tia tiếp tuyến và dây cung)
Xét tứ giác ABOC có:
(chứng minh trên)
(do AB là tiếp tuyến của (O) tại B)
(do AC là tiếp tuyến của (O) tại C)
(tổng bốn góc trong một tứ giác)
Lời giải:
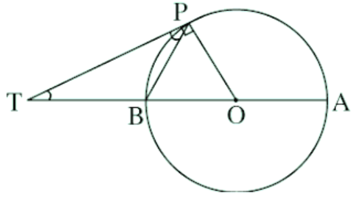
Góc TPB là góc tạo bởi tiếp tuyến PT và dây cung PB chắn cung nhỏ PB của đường tròn (O)
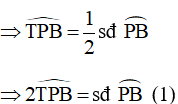
Lại có: Góc BOP là góc nội tiếp chắn cung PB của đường tròn (O) nên
![]()
Từ (1) và (2) ta suy ra:
PT là tiếp tuyến của đường tròn (O) tại P nên OP vuông góc với PT tại P
Xét tam giác TPO có:
Do đó, tam giác TPO vuông tại P
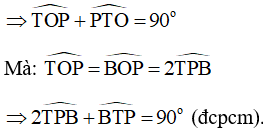
Lời giải:
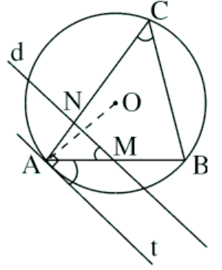
Vì: d // At (gt)
(hai góc so le trong) (1)
Ta có:
Góc BAt là góc tạo bởi tiếp tuyến At và dây cung AB chắn cung nhỏ AB của đường tròn (O)
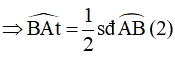
Góc ACB là góc nội tiếp chắn cung nhỏ AB của đường tròn (O)
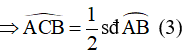
Từ (2) và (3) ta suy ra: (4)
Từ (1) và (4) ta suy ra:
Xét tam giác AMN và tam giác ACB có:
Góc A chung
(chứng minh trên)
Do đó, tam giác AMN đồng dạng với tam giác ACB (góc – góc)
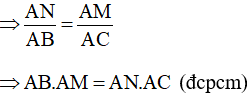
Lời giải:
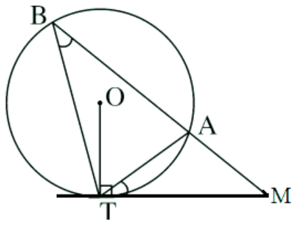
Xét đường tròn (O)
Góc TBA là góc nội tiếp chắn cung AT của đường tròn (O)
![]()
Góc ATM là góc tạo bởi tiếp tuyến TM và dây cung AT chắn cung nhỏ AT
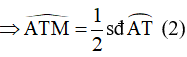
Từ (1) và (2) ta suy ra:
Xét tam giác BMT và tam giác TMA có:
Góc M chung
Do đó, tam giác BMT đồng dạng với tam giác TMA (góc – góc)
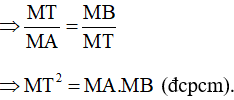
Hướng dẫn: Áp dụng kết quả của bài tập 34.
Lời giải:
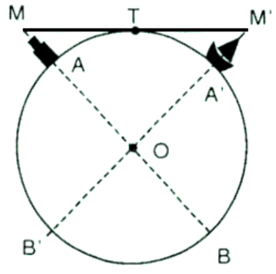
Đỉnh ngọn hải đăng là điểm M, vị trí mà người quan sát trên tàu là điểm M’.
O là tâm trái đất, M’A’ là khoảng cách từ người quan sát trên tàu tới mặt nước biển
MA là độ cao của ngọn hải đăng
MT là tiếp tuyến của đường tròn (O), MAB là cát tuyến của (O), theo kết quả bài 34 ta có:
Mặt khác, ta có:
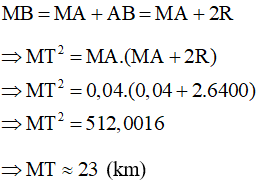
Ta lại có: M’T là tiếp tuyến của đường tròn (O), M’A’B’ là cát tuyến của (O), theo kết quả bài 34 ta có:
Mà:
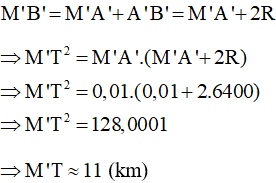
Do đó, (km).