Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 3 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung. Mời các bạn đón xem:
Bài tập Toán 9 Chương 3 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
A. Bài tập Góc tạo bởi tia tiếp tuyến và dây cung
I. Bài tập trắc nghiệm
Câu 1: Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Lời giải:
Cho đường tròn tâm (O) có Ax là tia tiếp tuyến tại điểm A và dây cung AB. Khi đó góc BAx là góc tạo bởi tia tiếp tuyến và dây cung
Chọn đáp án A
Câu 2: Góc tạo bởi tiếp tuyến và dây cung có số đo bằng
A. 90°
B. Số đo góc ở tâm chắn cung đó
C. Nửa số đo góc nội tiếp chắn cung đó
D. Nửa số đo cung bị chắn
Lời giải:
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng nửa số đo cung bị chắn
Chọn đáp án D
Câu 3: Kết luận nào sau đây là đúng
A. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo lớn hơn góc nội tiếp chắn cung đó
B. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo nhỏ hơn góc nội tiếp chắn cung đó
C. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau
D. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo bằng hai lần số đo của góc nội tiếp chắn cung đó
Lời giải:
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau
Chọn đáp án C
Câu 4: Cho nửa đường tròn (O) đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn . Gọi H là hình chiếu của C trên AB. CA là tia phân giác của góc nào dưới đây?
Chọn đáp án B
Câu 5: Cho nửa đường tròn (O) đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn . Gọi H là hình chiếu của C trên AB. Giả sử OA = a; MC = 2a . Độ dài CH
Chọn đáp án C
Câu 6: Cho đường tròn tâm (O), điểm M nằm ngoài đường tròn. Qua M dựng tiếp tuyến MA đến đường tròn (O), dựng cát tuyến MBC. Đẳng thức nào sau đây đúng ?
A. MA2 = MB.MC
B. MB2 = MA.MC
C. MC2 = MA.MB
D. 
Chọn đáp án A.
Câu 7: Cho đường tròn tâm O, đường kính AB, dựng tiếp tuyến Bx với đường tròn.
Lấy P là điểm bất kì trên đường tròn, AP cắt Bx tại T. Tìm khẳng định sai
Chọn đáp án B
Câu 8: Cho đường tròn (O) và dây BC = √2R. Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại A. Tính góc 
A. 45°
B. 30°
C. 60°
D. 750
Góc 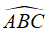là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC nên:
Chọn đáp án A.
Câu 9: Cho đường tròn (O; R) có dây BC không phải đường kính. Dựng hai tiếp tuyến tại B và C chúng cắt nhau tại A. Biết rằng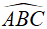 
= 30° . Tính BC theo R?
A. BC = √3R
B. BC = √2R
C. BC = R
D. Đáp án khác
Ta có:
Góc 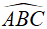là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC⌢ nên:
Chọn đáp án C.
Câu 10: Cho đường tròn (O; R) và dây BC. Dựng hai tiếp tuyến tại C và B cắt nhau tại A. Biết rằng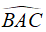 
= 60° . Tính AB
A. R
B. R√3
C. R√2
D. 2R
Câu 11: Cho tam giác ABC nội tiếp đường tròn (O), tiếp tuyến tại A của (O) cắt BC tại P. Hai tam giác nào sau đây đồng dạng?
A. ∆PAB ~ ∆ABC
B. ∆PAC ~ ∆PBA
C. ∆PAC ~ ∆ABC
D. ∆PAC ~ ∆PAB
Chọn đáp án B.
Câu 12: Cho tam giác MNP nội tiếp đường tròn (O), tiếp tuyến tại M của (O) cắt NP tại E. EM = 4cm. Tích EP. EN bằng:
A. 16cm2
B. 8cm2
C. 12cm2
D. 4cm2
Xét (O) có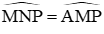 
(góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung MP)
Xét ∆EPM và ∆EMN có 
Suy ra ∆EPM ~ ∆EMN (g – g) suy ra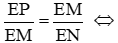 
EP. EN = EM2 = 42
= 16 (cm2)
Đáp án cần chọn là: A
Câu 13: Cho nửa đường tròn (O); đường kính AB và một điểm C trên nửa đường tròn. Gọi D là một điểm trên đường kính AB; qua D kẻ đường vuông góc với AB cắt BC tại F, cắt AC tại E. Tiếp tuyến của nửa đường tròn tại C cắt EF tại I. Khi đó:
A. IE = IF
B. IE = 2IF
C. EF = 2IE
D. EF = 3IF
Đáp án cần chọn là: A
Câu 14: Cho đường tròn (O; R) với A là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy điểm M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). Gọi I là trung điểm MA, K là giao điểm của BI với (O). Tam giác IKA đồng dạng với tam giác:
A. IBA
B. IAB
C. ABI
D. KAB
Đáp án cần chọn là: B
Câu 15: Cho tam giác nhọn ABC nội tiếp (O). Kẻ tiếp tuyến xAy với (O). Từ B kẻ BM // xy (M ∈ AC). Khi đó tích AM. AC bằng
A. AB2
B. BC2
C. AC2
D. AM2
Đáp án cần chọn là: A
II. Bài tập tự luận có lời giải
Câu 1: Cho đường tròn (O; R) với A là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy điểm M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). Gọi I là trung điểm MA, K là giao điểm của BI với (O). Giả sử MK cắt (O) tại C. Đường thẳng MA song song với đường thẳng
Lời giải:
Nên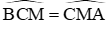 
mà hai góc ở vị trí so le trong nên MA // BC
Câu 2: Cho đường tròn (O; R) với A là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy điểm M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). Gọi I là trung điểm MA, K là giao điểm của BI với (O). Tam giác nào dưới đây đồng dạng với tam giác IKM?
Lời giải:
III. Bài tập vận dụng
Câu 1: Cho đường tròn (O) và điểm M nằm ngoài đường tròn, từ M vẽ cát tuyến MAB đến đường tròn. C là điểm trên đường tròn khác A và B. Chứng minh rằng MC là tiếp tuyến của đường tròn (O) khi và chỉ khi MC2 = MA.MB .
Câu 2: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D.
Chứng minh AB2 = BD.BC
B. Lý thuyết Góc tạo bởi tia tiếp tuyến và dây cung
1. Định nghĩa
- Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn, một cạnh là một tia tiếp tuyến còn cạnh kia chứa dây cung của đường tròn.
Ví dụ 1. Cho đường tròn (O) có xy là tiếp tuyến của đường tròn (O) tại A và dây cung AB như hình vẽ.
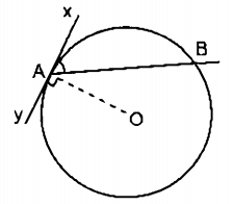
Ta thấy có đỉnh A nằm trên đường tròn (O) có Ax là tiếp tuyến và AB là dây cung của đường tròn.
Do đó là góc tạo bởi tiếp tuyến và dây cung.
Khi đó, chắn cung nhỏ AB;
chắn cung lớn AB.
2. Định lí
Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
Ví dụ 2. Cho đường tròn (O) có xy là tiếp tuyến của đường tròn (O) tại A và dây cung AB như hình vẽ.
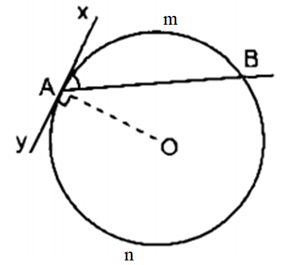
Khi đó, và là góc tạo bởi tiếp tiếp và dây cung lần lượt chắn và . Do đó,
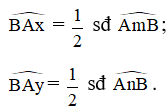
3. Hệ quả
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Ví dụ 2. Cho đường tròn (O) như hình vẽ.
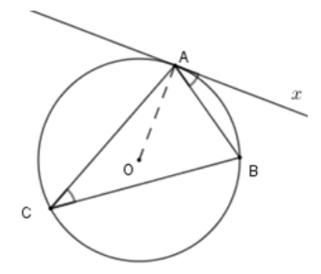
Trong hình vẽ trên, là góc nội tiếp chắn nên
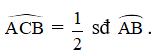
là góc tạo bởi dây cung và tiếp tuyến chắn nên
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
