Với giải Bài 31 trang 79 Toán lớp 9 chi tiết trong Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
Bài tập 31 trang 79 SGK Toán lớp 9 Tập 2: Cho đường tròn (O; R) và dây cung BC = R . Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính .
Lời giải:
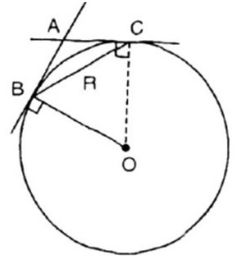
Xét tam giác OBC có:
OB = OC = BC = R
Do đó, tam giác OBC là tam giác đều
Mà góc BOC là góc ở tâm chắn cung nhỏ BC của đường tròn (O)
Ta có: là góc tạo bởi tia tiếp tuyến BA và dây cung BC chắn cung nhỏ BC
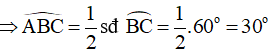
(định lý về góc tạo bởi tia tiếp tuyến và dây cung)
Xét tứ giác ABOC có:
(chứng minh trên)
(do AB là tiếp tuyến của (O) tại B)
(do AC là tiếp tuyến của (O) tại C)
(tổng bốn góc trong một tứ giác)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
